План практических и лабораторных занятий в гр. МиАПП-5 на весенний семестр 2015-2016 уч. Года.
В семестре 17 недель. Учебным планом предусмотрено 2 часа, т.е. одно практическое или лабораторное занятие в неделю. Всего получается 8 практических, 9 лабораторных занятий.
Лабораторные работы.
1. Фотометрия
2. Исследование тонких линз
3. Изучение аберраций в линзах
4. Интерференция в тонких пленках (кольца Ньютона)
5. Интерференция в бипризме
6. Дифракция на щели, принцип Бабине
7. Дифракционная решетка
8. Изучение законов теплового излучения
9. Отражение света на плоской границе, измерение угла Брюстера.
Планируем в семестре 2 типовых расчета: «Геометрическая оптика и интерференция», «Дифракция и квантовая оптика». На подготовку к каждому из них требуется по 2 практических занятия (всего 4 занятия). Оставшиеся 4 занятия распределяются для освоения «трудных» тем.
Одна из таких тем – волновое движение, электромагнитные волны (тема 17 в задачнике Ветровой) рассматривается на первом практическом занятии.
| Вариант | х1 | х2 | Δφ | k |
| ? | π | 0.628 | ||
1. Задача 17,3. Разность фаз двух колеблющихся точек, находящихся соответственно на расстоянии х1 и х2 от источника колебаний, составляет Δφ. Волновое число, соответствующее данной волне, равно k. Найти неизвестную величину согласно номеру в таблице, определить длину волны.
Решение: Волновое уравнение имеет вид z=Zmcos(ωt-kx). Величина под знаком cos – это фаза волны. Из условия задачи 
. Из четырех величин, входящих в это уравнение три заданы, находим четвертую.
Связь волнового числа и длины волны: k=2π/λ. При известном k находим λ.
| Вариант | ε | Em (В/м) | Hm (А/м) | V (м/с) |
| ? | ? | 8.56*10-3 | 1.86*108 | |
2. Задача 17.6. В однородной изотропной среде с относительной диэлектрической проницаемостью ε и относительной магнитной проницаемостью μ, близкой к единице, распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля волны равна Еm амплитуда напряженности магнитного поля - Hm, Фазовая скорость распространения волны— v. Найти неизвестные величины согласно номеру задания.
Решение: Соотношение между амплитудами напряженностей электрического и магнитного поля в ЭМ волне имеет следующий вид: Em/Hm=Z, где Z – волновое сопротивление среды, которое, в свою очередь, определяется формулой 
. В нашем случае μ=1. Скорость распространения волны 
. Таким образом из 5 величин заданными являются 3. Для нахождения двух оставшихся мы имеем 2 уравнения:
3. Задача 17.9. В вакууме распространяется плоская электромагнитная волна, в которой напряженность электрического поля меняется по закону Е == Еmcos(ωt-kx), а напряженность магнитного поля — по закону H= Нmcos (ωt-kx). Найти мгновенное значение величины вектора Умова-Пойнтинга в точке x1 в момент времени t и ее среднее за период и максимальное значение. Изобразить векторы напряженностей и Пойтинга в пространстве, когда они имеют максимальные значения.
| Вариант | x1 (м) | Em (В/м) | ω (1/с) | k (1/м) | t1 (с) |
| 1.2 | 2.5π*108 | 0.83π | 4.67*10-9 | ||
Решение: Мгновенное значение вектора Пойтинга определяется формулой
. Напряженность магнитного поля определится через напряженность электрического: Н=Е/Z, где Z волновое сопротивление среды, для вакуума Z=377 Ом. Поскольку векторы Е и Н взаимно перпендикулярны, модуль их векторного произведения равен произведению модулей. Таким образом, П=Е2/Z. Остается подставить данные задачи. Минимальное значение вектора Пойтинга равно нулю. Оно возникает в тех точках пространства и в те моменты времени, когда фаза колебаний (ωt-kx)=(2n+1)π/2, n – целое. Среднее значение модуля вектора Пойтинга определяется средним значением функции cos2(ωt-kx)=1/2. Поэтому <П>= П=Еm2/(2Z).
4. Из воздуха на плоскую поверхность стекла перпендикулярно падает ЭМ волна с интенсивностью I. Показатель преломления стекла n=1.5 (для разных вариантов разные n). Определить интенсивность отраженной и прошедшей в стекло волн.
Решение. При отражении ЭМ волны от границы раздела для амплитуды напряжённости электрического поля отраженной волны выполняется соотношение:
В котором, Z1 и Z2 – волновые сопротивления соответственно первой и второй сред. Волновое сопротивление среды можно выразить через коэффициент преломления: Z=Z0/n, где Z0 – волновое сопротивления вакуума (Z0 = 377 Ом). Тогда
Связь амплитуды напряженности электрического поля волны с ее интенсивностью определяется теоремой Пойтинга:
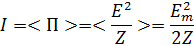
Подставим сюда формулу для амплитуды отраженной волны:
Интенсивность волны, прошедшей в стекло определится очень просто:
Типовые расчеты.
Т.Р. №4 Геометрическая оптика, интерференция света – задача №7 Чопчица, (задания 1, 2,3, 4, 6, 7).
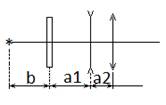Пример решения 99 вариант. Схема оптической системы показана на рисунке, а исходные данные – в таблице
| вариант | R1, м | R2, м | R3, м | R4, м | һ, см | D, мм | a1, см | a2, см | b, см | α | Тип билинзы | ε, мм | λ, нм | к.п.9 |
| 0,25 | 0,55 | 0,65 | 0,85 | 8,5 | 4,0 | 6,5 | 4,5 | 1200 | 6б | 0,25 | 9а |
Найти фокусные расстояния и оптические силы линз.
Формула, определяющая оптическую силу:
Где R1, R2 – радиусы кривизны соответственно левой и правой поверхностей линзы. Радиус положителен, если центр кривизны правее центра линзы. Радиус отрицателен, если центр кривизны левея центра линзы.
Для линзы 1 
Фокусные расстояния f1=1/D=0.273 м.
Для линзы 3 
Фокусные расстояния f3=1/D=-0.578 м.
Пункт 1 выполнен.
2. Найти положение изображения источника.
На плоскую пластинку падает расходящийся пучок, следовательно, пластинка приблизит к себе изображение источника на расстояние
После того, как мы учли действие пластинки ее можно удалить из оптической схемы, приблизив источник света к линзам на расстояние Δ. В результате получим схему, показанную на рисунке. Определим изображение источника, даваемое системой из двух линз, путем двукратного применения формулы тонкой линзы. Поместим начало координат в центр рассеивающей линзы. Координата источника света будет равна
xs=-(a1+b-Δ)=-68.67см.
Координата его изображения, даваемого рассеивающей линзой определится из формулы линзы:
Изображение получается слева от линзы. Следовательно, изображение мнимое. Определим коэффициент поперечного увеличения.
Увеличение положительно, следовательно, изображение не перевернуто. Поскольку Г меньше 1, изображение уменьшено.
Найдем параметры изображения источника, даваемое обеими линзами. Для этого изображение от рассеивающей линзы считаем предметом для второй линзы. Поместим начало координат в центр положительной линзы. Координата предмета для нее будет равна
Координата изображения:
Изображение будет справа от линзы, оно действительное.
Вычислим коэффициент поперечного увеличения:
Увеличение отрицательно, следовательно, изображение перевернуто. Модуль увеличения больше единицы, следовательно, изображение увеличенное.
Таким образом, данная оптическая система дает изображение источника света справа от собирающей линзы на расстоянии 111.5 см от нее. Изображение действительное, перевернутое, увеличенное. Общий коэффициент поперечного увеличения равен Г=Г1*Г3=-2.2.
Задание 2 выполнено.
Задание 3. Расстояние до экрана l не задано в таблице. Зададим его сами, например, 70 см. Найдем диаметр светлого пятна на экране, даваемого 
источником света. Диаметр линз, согласно данным варианта равен 4 мм. Принцип определения диаметра пятна показан на рисунке.
Из подобия треугольников
Найдем
Задание 3 выполнено
Задание 4 уже выполнено в ходе пункта 2.
Задания 6, 7. Задание выбрать самостоятельно расстояния от билинзы до источника света – xs и от билинзы до экрана – L является очень коварным. Если взять их произвольно, то можно вообще не получить интерференцию или получить число интерференционных полос меньше 1, что эквивалентно отсутствию интерференции. Поэтому выбор расстояний должен основываться на предварительном расчете интерференционной картины. После этого, используя полученные формулы, можно сделать выбор расстояний.
Для получения интерференционной картины необходимо обеспечить перекрытие световых потоков, формируемых каждой из половинок билинзы.
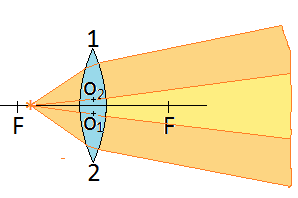
Источником света является ярко освещенная щель, находящаяся в плоскости разреза билинзы. Во всех случаях для получения интерференционной картины необходимо обеспечить перекрытие световых потоков, формируемых каждой из половинок билинзы. На рисунке показаны только два из четырех возможных вариантов расположения источника света относительно билинзы.
В случае сдвижной билинзы можно располагать источник в любом месте между линзой и точкой удвоенного фокусного расстояния до нее. Однако, если источник расположен за точкой фокуса перекрытие световых потоков полулинз оказывается в небольшой области между линзой и точкой фокуса. Интерференционная картина будет мелкой. Если же расположить источник между линзой и точкой фокуса (рис. 1) перекрытие световых потоков полулинз охватывает все расстояние за ней в угле расхождения лучей от источника в оптические центры полулинз.
Если используется раздвижная полулинза, источник света должен располагаться отностиельно линзы за точкой ее фокуса (рис. 2). Только в этом случае возможно перекрытие световых потоков полулинз в области того же угла, образованного лучами источника, проходящими через оптические центры полулинз. На рис. 1 и 2 область перекрытия световых
 |
потоков полулинз выделена более светлым тоном.
 |
Определение ширины интерференционной полосы проще всего сделать путем сведения оптической схемы билинзы к оптической схеме Юнга. Для этого определяются координаты двух вторичных источников света, которые являются изображениями исходного источника, даваемое каждой из полулинз. Расположим начало координат в центре билинзы и направим ось Х вдоль главной оптической оси. Координату х источника света – S обозначим xs, она отрицательна, а координату его изображения в полулинзах – через xs’. Все точки указаны на рис. 3.
Координаты изображений источника света определяются формулой линзы, которая справедлива в обоих случаях:
Расстояние между S1 и S2 вычислим из подобия треугольников SAB и SS1S2, причем в обои случая получается одна и та же формула.
Заменим xs’ его выражением (1) и получим окончательную формулу для d:
Возможны отрицательные значения d. В последующем будет переход к модулю.
Ширина интерференционных полос определится по формуле для опыта Юнга:
Где λ – длина световой волны, даваемой источником.
Для вычисления количества интерференционных полос необходимо ширину картины поделить на ширину полосы. Ширина картины – это ширина области перекрытия интерферирующих потоков, обозначенная на рисунке 3 через «у». Она найдется из подобия треугольников SMK и SAB:
Теперь определим количество полос в интерференционной картине:
После подстановки формулы для d получим:
Данная формула справедлива для обоих случаев билинзы. Поскольку экран во всех случаях находится правее изображений источника, разности (L-xs) и (L-xs’) всегда положительны. Единственным множителем, который может быть отрицательным является (xs+f), его и следует записать в виде модуля.
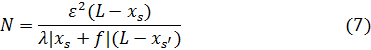
Рассмотрим отдельно случаи сдвижной и раздвижной билинзы.
Для сдвижной билинзы источник света может располагаться в фокальной плоскости. При этом его изображения по оси х оказываются в -∞. Ширина интерференционной картины остается конечной и, согласно (6), равной
Ширина интерференционной полосы также будет конечной. Полагая в (7) xs=-f, получим для числа полос простую формулу:
Теперь можем задаться желательным числом полос и вычислить необходимое для этого расстояние до экрана – L. Можно и наоборот, задать расстояние до экрана и определить получающееся на нем число интерференционных полос.
Для случая раздвижной билинзы нельзя расположить источник света в фокальной плоскости. Если это сделать, то изображения вторичных источников будут в +∞, а экран должен располагаться за ними, т.е. дальше, чем в ∞, что бессмысленно.
Из формулы (7) видно, что число полос в интерференционной картине будет тем больше, чем ближе расположен экран к изображениям источников, т.е. чем меньше величина L-xs’. Поэтому можно задавать произвольное расположение источника света в диапазоне (-2f<xs<-f) и подбором положения экрана, т.е. величины L-xs’получить требуемое количество полос в интерференционной картине.
Пусть для примера имеется линза с f=0.273м, расстояние между полулинзами ε=0.25 мм, длина волны λ=490 нм. Хотим получить 9 интерференционных полос. Зададим положение источника xs=-1.5f=-0.41м.
Из формулы (7) получим:
Из этого равенства при известном xs и вычисленном xs’ определится L=0.868 м.
Приведенные соображения позволят сделать выбор положения источника света и экрана, на котором наблюдается интерференционная картина, на основе заданного типа билинзы и желаемого числа интерференционных полос в картине.
