В данном пункте рассмотрено контактное напряженно-деформированное состояние конструкции опорной части с шаровым сегментом в сборе (рис. 3.3.). При построении модели сделаны следующие упрощения: исключены канавки со смазочным материалом, присутствующие на сферической и плоской поверхностях скольжения; элементы конструкции не обладающие осевой симметрией заменены на осесимметричные.
Задача решается численно в рамках математической постановки и алгоритма, приведенных в главе 2. Конструкция опорной части в сборе включает [47]: 1-3 – контактный узел, 4 –плоскую поверхность скольжения, 5 – верхнюю основную плиту (элемент), 6 и 7 – фартук, 8 – нижнюю плиту с полированным листом. Поверхности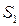 
и 
в конструкции в сборе являются контактными, помимо этого, добавляется еще ряд поверхностей контакта 
- 
.
Математическая постановка задачи анализа контактного напряженно-деформированного состояния опорной части с шаровым сегментом в сборе (рис. 3.3.) включает уравнения (2.1)–(2.3), контактные условия (2.8)-(2.11) на поверхностях контакта плит контактного узла со сферической прослойкой (
), контакта плит с плоской поверхностью скольжения (
), а также контакта между различными стальными деталями опорной части (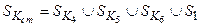
). Уравнения приведены при описании общей математической постановки задачи контакта. Полная поверхность контакта 
.
При этом постановка задачи дополняется физическими соотношениями деформационной теории упругопластичности, которая описыват поведение полимерного материала, они имеют вид [48]:
(3.1)
где 
– интенсивность тензора напряжений, 
– второй инвариант девиатора тензора напряжений 
, 
– интенсивность тензора деформаций, 
– второй инвариант девиатора тензора деформаций 
, 
– объемный модуль упругости, 
– функциональная зависимость, определяемая диаграммой деформирования материала прослойки при одноосном напряженном состоянии.
Постановка так же дополняется кинематическими граничными условиями на поверхности 
, 
, 
. (3.2)
Поверхность 
контактирует с очень жесткой конструкцией мостового пролета, что практически исключает поворот поверхности в пространстве, при этом интеграл по поверхности от компоненты силы 
равен прикладываемой вертикальной нагрузке. Таким образом, граничные условия на поверхности имеют вид:
, 
, , 
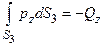, (3.3)
где 
– вертикальная сила, приложенная к , 
– неизвестная величина. Остальные наружные поверхности свободны от нагрузок.
По результатам расчета конструкции охарактеризуем особенности напряженно-деформированного состояния. Рассмотрим перемещения по координате 
и 
на поверхности (рис. 3.4.) в сравнении с перемещениями поверхности .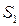
Перемещения на поверхности практически нулевые, следовательно, при исследовании ответственных частей конструкции опорной части с шаровым сегментом можно считать, что на поверхности 
и 
, таким образом плоскую поверхность скольжения можно не учитывать в модели контактного узла. При этом у поверхности 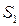перемещения 
практически одинаковы по радиусу. Следовательно, для упрощения можно принять, что поверхность 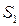в конструкции в сборе остается в процессе деформирования плоской.
Рассмотрим распределение давления на поверхности 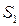в сравнении с давление в контактном узле (рис. 3.5.).
Для конструкции в сборе распределение давления на поверхности 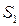неравномерное: максимум в центре с дальнейшим падением к краю прослойки, у края поверхности значения давления нулевые, что связанно с трением при контактном взаимодействия.
Рассмотрим относительное контактное давление и относительное контактное касательное напряжения (отнесено к прикладываемой нагрузке
) на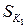 
(рис. 3.6.) для конструкции в сборе в сравнении с результатами для контактного узла 1-3.
Контактные давление и касательное напряжение в опорной части в сборе и в контактном узле не совпадают. Для конструкции в сборе максимальное контактное давление в зоне сцепления с дальнейшим понижением в зоне перехода контактных состояний сцепление-проскальзывание, к краю прослойки контактное давление продолжает падать. В контактном узле распределение относительного контактного напряжения неоднородно с ярко выраженными зонами максимума и минимума, при этом в зоне сцепления у конструкции в сборе оно меньше, чем у контактного узла. Относительное контактное давление в конструкции в сборе также отличается от случая контактного узла.
Данные отличия могут быть связаны с деформацией верхней плиты с шаровым сегментом, рассмотрим характер ее деформирования (рис. 3.7.).
Максимальные перемещения на 
по координате равны 
м, минимальные – 
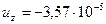. Следовательно, причиной столь неоднородного распределения относительных контактных давления и касательного напряжения на поверхности является осесимметричный изгиб относительно тонкой верхней стальной плиты, поверхность становится выпуклой вверх [49]. В сборе контактный узел не имеет возможности осесимметричного изгиба и поверхность остается плоской. Таким образом, граничные условия требуют уточнения.
Для модели контактного узла (рис. 3.8.) граничные условия включают:
кинематические граничные условия на поверхности 
, , 
, (3.4)
статические и кинематические граничные условия на поверхности
, 
, , 
, (3.5)
где – вертикальная сила, приложенная к , – неизвестная величина, а остальные наружные поверхности являются свободными от нагрузки.
Рассмотрим распределение давления на поверхности с новыми граничными условиями в контактном узле. На рис. 3.9. приведено распределение давления на для контактного узла в сравнении с конструкцией в сборе.
На большей части поверхности 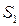давление имеет хорошее количественное совпадение для модели конструкции опорной части с шаровым сегментом в сборе и для модели контактного узла. У края поверхности значения давления разные, что связанно с трением при контактном взаимодействия, учтенном в конструкции в сборе.
Рассмотрим относительные контактное давление и контактное касательное напряжения на 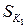(рис. 3.10.) для конструкции в сборе в сравнении с результатами для контактного узла, полученное при новых граничных условиях.
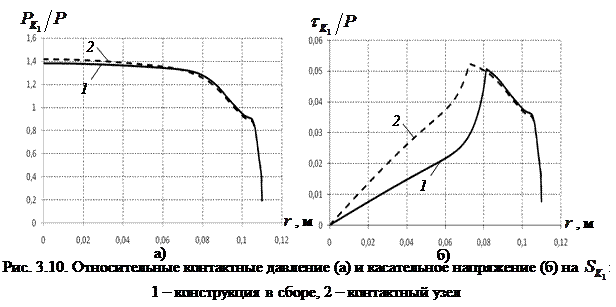
Контактное давление для двух вариантов рассмотрения конструкции опорной части с шаровым сегментом имеет хорошее качественное и количественное совпадение. Наблюдается (рис. 3.10.,б), что контактное касательное напряжение в зоне сцепления у конструкции в сборе меньше, чем у контактного узла, при этом протяженность зоны сцепления у конструкции в сборе больше. Данный эффект может быть связан с ужесточением контактного узла в сборке: плита 5 и фартук 6 ограничивают движение сферического сегмента. В зоне проскальзывания до края прослойки относительное контактное касательное напряжение имеет хорошее количественное и качественное совпадение для обоих вариантов решения. В целом контактное касательное напряжение меньше контактного давления и дает малый вклад в полное контактное напряженное состояние.
Характер деформирования верхней плиты в случае новых граничных условий показан на рис. 3.11.
Перемещение поверхности по координате составляет 
.
В результате исследования конструкции в сборе к граничным условиям из главы 2 добавлено дополнительное кинематическое ограничение на поверхности , что привело к малому количественному и качественному отличию результатов решения для контактного узла и для опорной части в сборе. Из ранее сказанного и рис. 3.9.-3.11. можно сделать вывод о возможности неучета в расчетной схеме части конструкции опоры с шаровым сегментом и исследовании только контактного узла, без учета плоской поверхности скольжения нижней плиты.
