
Рис. 3
На рисунке 3 изображено решение СЛАУ, при котором не выполнялось условие диагонального преобладания и видно, что достаточное условие сходимости не выполняется.

Рис. 4
На рисунке 4 изображено решение СЛАУ с выполнением условия диагонального преобладания. Видно, что достаточные условия сходимости выполняются.
К п.3. Необходимо в меню программы, не меняя ранее введенных настроек, ввести расширенную матрицу системы с диагональным преобладанием. Затем следует в пошаговом режиме счета убедиться, что итерации метода Якоби и Гаусса-Зейделя сходятся, т.е. выполняется принцип сжимающих отображений x=Fx, когда правая часть системы уравнений вида x=Сx+d определяет отображение F, при котором строится итерационная последовательность, сходящаяся к единственной неподвижной точке х.

Рис. 5
На рисунке 5 показаны результаты расчёта в пошаговом режиме СЛАУ итерационным методом Гаусса-Зейделя. Видно, что достаточное условие сходимости выполняется.

Рис. 6
На рисунке 6 показаны результаты расчёта СЛАУ в пошаговом режиме используя метод Якоби. Видно, что выполняются достаточные условия сходимости. Число итераций для получения ответа с нужной точность равнялось 21.
К п.4. Итерационный параметр (w) вводится для ускорения сходимости методов как дополнительное смещение компонент вектора решения x(k) на величину w
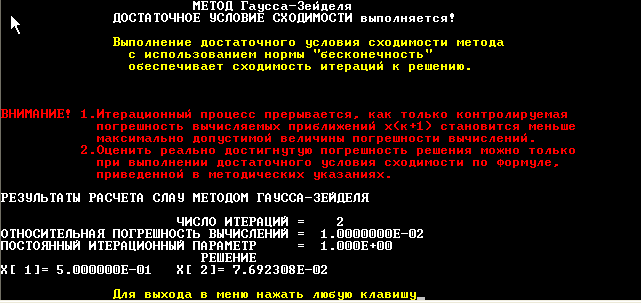
Рис. 7
На рисунке 7 показано решение СЛАУ методом Гаусса-Зейделя и подбором величины w. Видно, что решение с достаточной точностью было получено всего за 2 итерации.
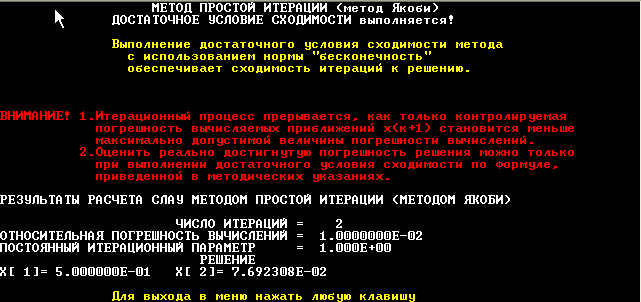
Рис. 8
На рисунке 8 показано решение СЛАУ методом Якоби и подбором величины w. Видно, что решение с достаточной точность было получено всего за 2 итерации
К.п.5. Необходимо в меню программы восстановить нулевое начальное приближение и изменить значение точности вычислений 10-3 на 10—10. Для расчета применить только метод Якоби. З афиксироват ь в рабочую тетрадь полученные результаты решения и число итераций.

Рис. 9
На рисунке 9 изображено решение СЛАУ порядка 3, итерационным методом Якоби. Видно, что достаточные условия сходимости выполняются. Относительная погрешность согласно условию, равняется 1*E-10. Число итераций для получения решения с заданной точностью = 38.
Вывод: итерационные методы эффективны в тех случаях, когда нужно получать значения с определённой точностью. Но итерационные методы не всегда сходятся. В случае, если итерационный метод не сходится, то стоит попробовать применить другой метод итераций.
Лабораторная работа №4
Интерполирование
Цель работы: закрепление знаний о полиномиальной интерполяции по формулам Лагранжа и Ньютона, а также о кубической сплайн-интерполяции; приобретение навыков оценки точности интерполяции.
Программа работы
1. Интерполировать табличную функцию для заданного числа узлов и значений функции и рассчитать значение интерполирующей функции в заданных точках по формулам 1.1. формула Лагранжа; 1.2. формула Ньютона; 1.3. формула кубической сплайн-функции
2. Повторить интерполяцию функции для измененного числа узлов и ее значений по формулам Лагранжа, Ньютона и кубической сплайн-функции и рассчитать значение интерполирующих функции в точках п.1.
3. Определить фактическую погрешность интерполяции результатов п.1 и 2. 4. Оценить максимально возможную величину погрешности полиномиальной интерполяции п.1.
Ход работы:
К п.1. Поскольку интерполируемая функция представлена последовательностью узлов (2) через неравные промежутки, то меню программы необходимо настроить на интерполирующую формулу Лагранжа общего вида,затем ввести количество узлов интерполяции –5, количество расчетных точек-3. Узлы интерполяции и значения функции в них ввести согласно указанию (2) в левом окне экрана, а расчетные точки интерполяции ввести согласно индивидуальному заданию в правом окне.
К п.1.1. Формула Лагранжа.

Рис. 1
На рисунке 1 показаны узлы интерполяции и их значения, а также точки интерполяции и рассчитанные значения функции.

Рис. 2
На рисунке 2 изображён график интерполяции функции формулой Лагранжа.
К п.1.2.Формула Ньютона.

Рис. 3
На рисунке 3 показаны узлы интерполяции и их значения, а также точки интерполяции и рассчитанные значения функции при помощи интерполирования полиномом Ньютона.

Рис. 4
На рисунке 4 изображён график интерполяции функции формулой Ньютона.
К п.1.3. Формула сплайн-функции.

Рис. 5
На рисунке 5 показаны узлы интерполяции и их значения, а также точки интерполяции и рассчитанные значения функции при помощи интерполирования Сплайнами. 
Рис. 6
На рисунке 6 изображён график интерполяции функции Сплайнами.
К п. 2. Увеличить количество точек интерполяции и сравнить результаты.
Для формулы Лагранжа:

Рис. 7
На рисунке 7 показаны узлы интерполяции и их значения, а также точки интерполяции и рассчитанные значения функции.

Рис. 8
На рисунке 8 изображён график интерполяции функции Сплайнами.
Сплайн интерполяция:

Рис. 9
На рисунке 9 показаны узлы интерполяции и их значения, а также точки интерполяции и рассчитанные значения функции.

Рис. 10
На рисунке 10 изображён график интерполяции функции Сплайнами. Из графика следует, что в некоторых случаях могут возникать осцилляции на границах сетки интерполяции.
Вывод: интерполяция функции возможна только при условии, что интерполируемый полином, будет того же порядка или выше, чем сама функция. В противном случае, могут возникать осцилляции на границах интерполяции. Интерполяция является очень мощным средством в численных методах и лежит в основе многих численных решений. Например, в численном интегрировании.
Лабораторная работа №5
Численное интегрирование
Цель работы: закрепление знаний о численном интегрировании по обобщенным формулам средних прямоугольников, трапеций, Симпсона, а также квадратурным формулам Ньютона-Котеса более высокого порядка точности, приобретение навыков оценки точности результата.
Программа работы
1. Вычислить определенный интеграл от заданной функции по заданному отрезку методами средних прямоугольников, трапеций, Симпсона с фиксированным числом частичных отрезков.
2. Вычислить определенный интеграл от заданной функции по заданному отрезку с фиксированным числом частичных отрезков, используя одну из квадратурных формул Ньютона-Котеса высокого порядка.
3. Вычислить определенный интеграл от заданной функции по заданному отрезку методами средних прямоугольников, трапеций, Симпсона с заданной максимально допустимой погрешностью.
4. Вычислить определенный интеграл от заданной функции по заданному отрезку с заданной максимально допустимой погрешностью, используя как в п.2 квадратурную формулу Ньютона-Котеса высокого порядка.
5. Определить фактическую погрешность расчетных значений п.1 и 2.
Ход работы:
К п.1. Расчеты по формулам дают точное значение интеграла в случае, если подынтегральная функция на отрезке [a,b] является соответственно полиномом степени 0,1 и 2. В противном случае точность расчета повышается применением обобщенных (составных) квадратурных формул, которые строятся следующим образом


Рис. 1
На рисунке 1 изображён расчёт интеграла методом средних прямоугольников с фиксированным шагом и числом узлов = 10. Относительная погрешность метода 2.23*E-04

Рис. 2
На рисунке 2 изображён расчёт интеграла методом трапеций с фиксированным шагом и числом узлов = 10. Относительная погрешность метода 4.48*E-04

Рис. 3
На рисунке 3 изображён расчёт интеграла методом Симпсона с фиксированным шагом и числом узлов = 10. Относительная погрешность метода 1.3*E-07
К п. 2. Расчет по формуле Ньютона-Котеса дает точное значение интеграла в случае, если подынтегральная функция на отрезке [a,b] является полином степени n-. В программе эта формула, как и в п 1. применяется к каждому частичному отрезку при делении всего отрезка [a,b] на N частей и называется составной формулой Ньютона-Котеса
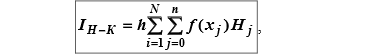
Составная формула Ньютона-Котеса

Рис. 4
На рисунке 4 показан расчёт интеграла методом Ньютона-Котеса с фиксированным шагом и числом отрезков = 10. Относительная погрешность метода 1,2*E-03
К п. 3. Необходимо меню программы настроить на тип расчета "с заданной точностью ", если необходимо, изменить величину относительной погрешности вычислений и оставить прежним режим расчета (пошаговый). Получить и зафиксировать значения интеграла, применяя методы средних прямоугольников, трапеций и Симпсона.
В отличие от расчета в п.1 расчет "с заданной точностью’ предусматривает для повышения точности интегрирования, уменьшение шага интегрирования h (длины частичного отрезка) последовательным увеличением числа частичных отрезков.

Рис. 5
На рисунке 5 изображён расчёт интеграла с заданной точность методом средних прямоугольников. Заданная точность обеспечивалась при разбиении отрезка интегрирования на 48 частей.

Рис. 6
На рисунке 6 изображён расчёт интеграла с заданной точностью методом трапеций. Заданная точность обеспечивалась при разбиении отрезка интегрирования на 192 частей.

Рис. 7
На рисунке 7 изображён расчёт интеграла с заданной точность методом Симпсона. Заданная точность обеспечивалась при разбиении отрезка интегрирования на 6 частей.
К п.4. В меню программы установить метод Ньютона-Котеса и выбранное в п.2 число узлов интерполяции. Не изменяя остальные настройки меню, провести визуальный анализ уточнения приближенных значений интеграла как в п. 3, фиксируя каждый шаг уточнения в рабочую тетрадь.

Рис. 8
На рисунке изображён расчёт интеграла с заданной точностью методом Ньютона-Котеса. Заданная точность обеспечивалась при разбиении отрезка интегрирования на 192 части.
Вывод: исследуя методы численного интегрирования в данной лабораторной работе, можно установить, что самым эффективным методом интегрирования, из выше перечисленных – это метод Симпсона. Во-первых потому что для экстраполяции функции он использует полином 2 порядка, во-вторых, что он обладает симметрией при интерполяции, как и метод прямоугольников.






