Лабораторная работа №1
Погрешность численных расчетов на ЭВМ
Цель работы: закрепление знаний о возникновении и влиянии на результаты расчета погрешности округления, приобретение умения ее практической оценки и навыков рациональной организации вычислений.
Программа работы
1. Определить машинное эпсилон (EPS) двумя способами (по итерационному алгоритму и по формуле); сравнить результаты, определить количество верных десятичных цифр в вещественных числах ЭВМ, характеризующихся полученным расчетным значением EPS.
2. Выявить в фрагменте программы некорректно записанные операторы и определить необходимые исправления; экспериментально обеспечить выполнение условия в условном операторе и рассчитать максимальную величину погрешности вычисления разности двух величин в условии.
3. Осуществить подбором коэффициентов квадратного уравнения заметного отличия двух значений одного и того же корня, вычисляемого по теоретически тождественным формулам, определить максимальную абсолютную погрешность и минимальное число верных десятичных цифр в расчетных величинах.
4. Подобрать значение переменной Х и число слагаемых n, обеспечивающие отличающиеся значения результата вычисления по заданному выражению и составной ее части (суммы) при различных способах суммирования (в порядке возрастания и убывания слагаемых), произвести анализ максимальной абсолютной погрешности округления двух расчетных значений сумм.
5. Подобрать значение слагаемого Х и число n2 слагаемых, обеспечивающие отличающиеся значения суммы, которая вычисляется двумя способами (последовательное суммирование n2 слагаемых и суммирование n групп из n слагаемых), произвести анализ максимальной абсолютной погрешности округления двух расчетных значений сумм.
Ход работы
 К п.1. Поставить на выполнение пункт меню EPS.
К п.1. Поставить на выполнение пункт меню EPS.
Рис. 1
Вычислили машинный эпсилон с помощью разных итерационных алгоритмов. И в результате проведённых оценок видно, что точные результаты может дать оценка по формуле. Оценка программная не точная, т.к. машинное эпсилон используемого представления данных в памяти не соответствует стандартам IEEE
К. п.2. Поставить на выполнение пункт меню LOOP. Вариант задачи определяется преподавателем. Результаты расчета фрагмента программы выводятся на экран для контроля ее правильной работы и не фиксируются в тетради.

Рис. 2
На рисунке 2 показан результат работы программы, а также результаты выполнения задания. В результате выполнения этого пункта была проведена оценка погрешности вычислений и определена нижняя граница интервала поиска
К п.3. Поставить на выполнение пункт меню SQR.
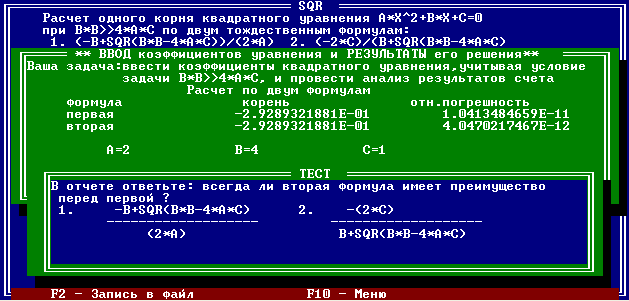
Рис. 3
На рисунке 3 показан результат выполнения пункта меню SQR. В результате выполнения этого пункта было установлено, что формула 2 даёт меньшую погрешность при вычислении квадратного корня практически во всех случаях.
К п.4 и 5. Поставить на выполнение пункт меню SUMMA. В этом пункте численные эксперименты содержат вычисления сумм. Полезно учесть при проведении в этом пункте двух численных экспериментов, что зависимость погрешности результата суммирования от числа слагаемых является немонотонной (не всякое увеличение числа слагаемых приводит к заметным различиям вычисленных значений двумя способами).
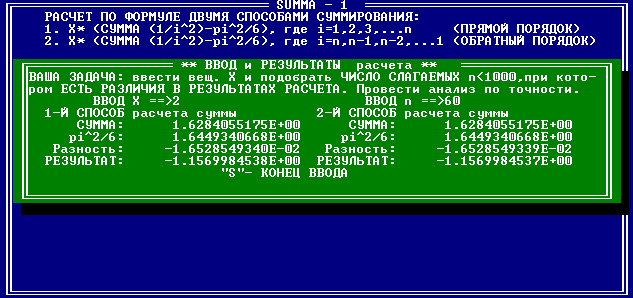
Рис. 4
На рисунке 4 показано, что обратный порядок решения даёт меньшую погрешность вычисления.
Вывод: На погрешность вычислений влияет в первую очередь используемый метод, разрядность представления чисел в памяти и способ округления. Во вторую очередь влияют математические операции и округление в разные стороны.
Лабораторная работа №2
Решение систем линейных алгебраических уравнений прямыми методами.
Цель работы: закрепление знаний о методе Гаусса и Жордана (Гаусса – Жордана), о роли выбора ведущего элемента и о влиянии числа обусловленности; приобретение умений практической оценки погрешности решения СЛАУ, обусловленной округлением; получение навыков оценки чувствительности решения СЛАУ к изменению исходных данных системы.
Программа работы:
1. Решить СЛАУ методами Гаусса и Жордана без выбора ведущего элемента, фиксируя результат каждого шага преобразования исходной матрицы.
2. Решить СЛАУ методом Гаусса с различными способами выбора ведущего элемента.
3. Оценить максимально возможную величину погрешности результатов п.2., обусловленную погрешностью округления.
4. Определить при заданном изменении элементов столбца правых частей, используя метод Гаусса с выбором ведущего элемента по столбцу, фактическое относительное изменение решения СЛАУ и его максимальную величину.
5. Определить при заданном изменении элементов матрицы, используя метод Гаусса с выбором ведущего элемента по столбцу, фактическое относительное изменение решения СЛАУ и его максимальную величину.
Ход работы.
К п.1. Необходимо решить СЛАУ вида Ax=b сначала методом Гаусса, затем Жордана. Меню программы следует настроить в соответствии с рекомендациями п. Общие, установив метод Гаусса без выбора ведущего элемента и пошаговый режим расчета для детального уяснения операций каждого шага преобразования расширенной матрицы для исходной СЛАУ. В рабочей тетради не фиксировать на прямом ходе результаты промежуточных операций, а только элементы расширенной матрицы после каждого шага исключения неизвестных. Результаты обратного хода метода Гаусса зафиксировать в порядке определения неизвестных. При этом учитывать, что без выбора ведущего элемента не всегда можно определить решение СЛАУ с невырожденной матрицей, т.к. может оказаться, что ведущий элемент - нулевой.

Рис. 1
На рисунке 1 решение СЛАУ методом Гауса без выбора ведущего элемента.

Рис. 2
На рисунке 2 изображено решение СЛАУ методом Жордана без выбора ведущего элемента.
К п.2. Решить СЛАУ методом Гаусса с различными способами выбора ведущего элемента.

Рисунок 3. Решение СЛАУ методом Гауса с выбором ведущего элемента по строке.

Рисунок 4. Решение СЛАУ методом Гауса с выбором ведущего элемента по столбцу.

Рисунок 5. Решение СЛАУ методом Гауса с выбором ведущего элемента
по всей матрице.
К п.3. Оцениваем максимально возможную величину погрешности результатов, обусловленную погрешностью округления.

Рисунок 6. Число обусловленности COND(A)=80.62
К п.4. Определить при заданном изменении элементов столбца правых частей, используя метод Гаусса с выбором ведущего элемента по столбцу.

Рисунок 7. Решение СЛАУ методом Гауса с выбором ведущего
элемента по столбцу правых частей.
К п.5. Определить при заданном изменении элементов матрицы, используя метод Гаусса с выбором ведущего элемента по столбцу и его максимальную величину.

Рисунок 8. Решение СЛАУ методом Гауса с выбором ведущего элемента
по столбцу и его максимальная величина.
Вывод: вычисления больших матриц с очень большим числом неизвестных может привести к накоплению погрешности и в результате к неточности вычислений. Выбор ведущего элемента при использовании метода Жордана и метода исключения Гаусса практически не приводит к уменьшению погрешности вычислений, за исключением некоторых случаев. Так же результаты вычислений зависят от числа обусловленности матрицы. Если матрица плохо обусловлена, то прямой метод будет давать большую погрешность при вычислениях неизвестных.
Лабораторная работа №3
Решение систем линейных алгебраических уравнений итерационными методами.
Цель работы: закрепление знаний о методах простой итерации и Гаусса-Зейделя; о достаточном условии и характере сходимости методов, о влиянии на скорость сходимости итерационного параметра, начального приближения, заданной максимально допустимой точности вычислений. Приобретение умений эквивалентных преобразования СЛАУ для обеспечения достаточного условия сходимости, а также приобретения навыков практической оценки фактической погрешности решения СЛАУ
Программа работы
1. Проверить для варианта задания СЛАУ лабораторной работы №1 достаточное условие сходимости метода Якоби и метода Гаусса-Зейделя и независимо от результата проверки произвести попытку решения СЛАУ.
2. Обеспечить выполнение достаточного условия сходимости путем эквивалентных преобразований исходной СЛАУ
3. Решить преобразованную в п.2 СЛАУ исследуемыми методами и оценить максимально возможную величину погрешности решения, обусловленную каждым из используемых методов.
4. Определить оптимальное значение итерационного параметра для каждого используемого метода, обеспечивающего минимальное число итераций.
5. Определить влияние выбора начального приближения на число итераций и точность решения.
6. Определить влияние погрешности округления на сходимость итерационного процесса с заданной точностью.
Ход работы:
К п.1. Проверить для варианта задания СЛАУ лабораторной работы №1 достаточное условие сходимости метода Якоби и метода Гаусса-Зейделя и независимо от результата проверки произвести попытку решения СЛАУ

Рис. 1
На рисунке 1 изображено решение СЛАУ итерационным методом Якоби.

Рис. 2
На рисунке 2 изображено решение СЛАУ итерационным методом Гаусса-Зельделя.
Видно, что метод Гаусса-Зейделя даёт нужный результат за меньшие число итераций, в данном конкретном случаи.






