Порядок выполнения работы
Определите приблизительно максимальное и минимальное значение функции F (x) на заданном отрезке. Запишите это приближенное значение в любую свободную ячейку. Относительно этого значения запишите функцию (желательно в ячейке справа от аргумента). С помощью команды Поиск решения найдите максимум и минимум вашей функции.
Сделайте выводы по всем методам поиска и найденным значениям.
Приложение 2
Построение графика системы уравнений.
1. Построить
 на[-2;1,5]с шагом 0,1
на[-2;1,5]с шагом 0,1
Решение:
а) Табулируем систему уравнений.
В ячейку А9 пишем слово аргумент,
в В9 вводим слово функция;
в А10 записываем - 2, в А11 - 1,9
и заполняем до - А45 автозаполнением.
б) В ячейку В10 записываем систему уравнений в виде, принятом в Excel.
=ЕСЛИ(А10<0;А10^2;ЕСЛИ(А10=0;0;КОРЕНЬ(А10))) и распространяем ее до В45 автозаполнением.
в) По столбцу В строим график (ход построения подробно описан в приложении 5)
Полученный график системы уравнений

Приложение 3
Решение систем линейных уравнений
I Решение систем линейных уравнений методом Крамера.
Пусть задана система линейных уравнений

Неизвестные x1, x2, …, xn вычисляются по формулам:

D – определитель матрицы А,
Di – определитель матрица, полученный из матрицы А путем замены i -го столбца вектором b.
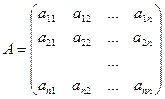 ,
,  ,
,  ,
,  ,
,
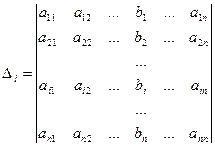 .
.
Пример 1. Решить систему линейных уравнений методом Крамера.

Запишем в табличном процессоре Microsoft Office Excel 2007 матрицы, которые понадобятся нам при вычислениях (рис. 43).

Рис. 43. Исходные данные
Найдем определители D, D1, D2, и D3, используя математическую функцию МОПРЕД (рис. 44).

Рис. 44. Вычисление определителей
Корни уравнения найдем по формулам: 
В результате всех вычислений должны получиться следующие данные:

Рис. 45. Вычисление корней системы уравнений
II Решение систем линейных уравнений матричным методом
Пусть дана система линейных уравнений

Эту систему можно представить в матричном виде: А·Х=В, где
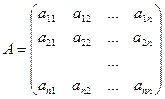 ,
,  ,
,  .
.
Умножим систему линейных алгебраических уравнений А·Х=В слева на матрицу, обратную к А. Тогда система уравнений примет вид:
А-1·А·Х=А-1·В.
Так как А-1·А=Е (единичная матрица), то получим Е·Х=А-1·В.
Таким образом, вектор неизвестных вычисляется по формуле: Х=А-1·В.
Пример 2. Решить систему линейных уравнений матричным методом.

Запишем в табличном процессоре матрицу А и столбец свободных
членов В (рис. 46).

Рис. 46. Исходные данные
Нам необходимо найти обратную матрицу А-1, для этого:
1. выделите диапазон ячеек В8:D10;
2. вызовите функцию МОБР;
3. в появившемся диалоговом окне заполните поле ввода Матрица. Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица, то есть В2:D4, нажмите кнопку ОК;
4. В первой ячейке выделенного диапазона появиться некоторое число. Чтобы получить всю обратную матрицу, необходимо нажать клавишу F2, для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter (рис. 47).

Рис. 47. Обратная матрица
Осталось найти вектор неизвестных по формуле Х=А-1·В, для этого:
1. выделите диапазон ячеек G8:G10;
2. вызовите функцию МУМНОЖ;
3. в поле для первой матрицы укажите диапазон В8:D10;
4. в поле для второй матрицы укажите диапазон G2:G4;
5. нажмите кнопку ОК.
В результате должны получиться следующие значения:

Рис. 48. Вычисление корней системы уравнений
Самостоятельно сделайте проверку, для этого умножьте матрицу А на Х. В результате должен получиться столбец В.






