Теоретичні відомості
Якщо абсолютна похибка не залежить від значення вимірюваної величини, то вона називається адитивною - такою, що додається під час вимірювання величини (рис. 9.1, а). Відповідно до означення її модель
(6.1)
а результат вимірювання, що спотворений адитивною похибкою 
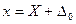(6.2)
Адитивні похибки проявляються як зміщення покажчика аналогових приладів з нульової позначки, а в електронних приладах — як ненульовий показ при нульовому значенні вимірюваної величини.
Очевидно, що відносне значення адитивної похибки зростає зі зменшенням вимірюваної величини
(6.3)
Якщо абсолютна похибка прямо пропорційно залежить від значення вимірюваної величини, то вона називається мультітлікативною (рис. 9.1, б). Відповідно до означення її модель
(6.4)
де 
— відносна мультиплікативна похибка, а результат вимірювання, що спотворений такого похибкою
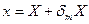(6.5)
Для нульового значення вимірюваної величини ця похибка також має нульове значення. Мультиплікативна похибка вимірювання зумовлена похибками коефіцієнтів перетворення вимірювальних перетворювачів, зокрема масштабних — вимірювальних підсилювачів, подільників, трансформаторів. Похибки еталонних (зразкових) величин можуть також сприяти виникненню мультиплікативних похибок.
Наприклад, похибка ЕРС нормального елемента при вимірюванні компенсатором спричиняє мультиплікативну похибку, як і похибка зразкового резистора у
Рис. 5. Адитивна (а, г), мультиплікативна (б, д) та нелінійна похибки (в, е)
шестиплечому мості. Загалом мультиплікативні похибки спричинені похибками (зміною) чутливості елементів вимірюваного кола.
Відносна мультиплікативна похибка є сталою незалежною від значення вимірюваної величини
(6.6)
Похибка вимірювань може складніше залежати від вимірюваної величини, наприклад, квадратично чи за іншим законом (рис. 9.1, в). У такому разі говорять про нелінійну похибку 
і результат вимірювання, що її містить, становить
(6.7)
зокрема за квадратичної похибки –
(6.8)
де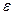 
— коефіцієнт, що визначає вплив квадратичної нелінійної похибки.
Нелінійні похибки виникають, якщо у вимірюваннях застосовується ЗВТ з нелінійними характеристиками, а також внаслідок трансформації адитивних та мультиплікативних похибок при нелінійних залежностях між вимірюваними величинами, зокрема під час опосередкованих, сумісних та сукупних вимірювань.
Відносна нелінійна похибка залежить від значення вимірюваної величини. Зокрема, для квадратичної похибки її відносне значення лінійно зростає зі збільшенням вимірюваної величини
(6.9)
Якщо залежності рівнянь вимірювань нелінійні, може відбуватися трансформація як адитивних в мультиплікативні похибки, так і їх обох в нелінійні.
У практиці вимірювань всі перелічені складові можуть спотворювати результат вимірювання, тобто
(6.10)
За певних умов деякими складовими можна знехтувати і розглядати лише одну чи дві складові. Наприклад, під час вимірювання струму похибка опору шунта спричиняє здебільшого мультиплікативну похибку (адитивною та нелінійного похибками шунта зазвичай нехтують).
Стосовно віднесення похибки квантування до тієї чи іншої групи існують взаємно протилежні думки: її часто наводять як приклад адитивних, і, забігаючи вперед, ще й випадкових. Це зумовлено тим, що похибка квантування уздовж всього діапазону вимірювання набуває значення у обмеженій сталій смузі, тобто граничні значення похибки квантування є сталими і у цьому розумінні їх можна вважати адитивними. Як буде показано нижче, де йтиметься про коригування (виправлення) адитивних та мультиплікативних похибок, власне наявність похибки квантування, як і інших нелінійних похибок, обмежує ефективність коригування. Отже, це типовий приклад нелінійної, майже періодичної при зміні вимірюваної величини, похибки, правда, з певними специфічними особливостями.
Задача 31. Систематична адитивна похибка цифрового омметра певного типу для заданих умов його роботи пронормована граничними значеннями 
від границі вимірювання. Який зміст цього запису? Знайти границі абсолютної адитивної похибки омметра.
Розв’язання Цей запис означає, що для заданих умов роботи цифрового омметра цього типу не вийде за границі 
від межі вимірювання 
.
Тобто границі абсолютної адитивної похибки омметра
Задача 32. Нормально розподілена випадкова адитивна похибка підсилювача для заданих умов його роботи пронормована стандартним відхиленням 
. Який зміст цього запису?
Цей запис означає, що для заданих умов роботи адитивна випадкова похибка підсилювача може змінюватися випадково, однак для достатньо тривалих спостережень її значення має стандартне (середиьоквадратичне) відхилення , на основі якого можна розраховувати довірчі границі випадкової похибки.
Задача 33. У заданий момент часу поточний час годинника встановлено з похибкою 
. Нестабільністю ходу годинника знехтувати. Яке значення набуде адитивна похибка від неправильного встановлення часу через 1 год? через 10 год?
Разе’язання. Оскільки хід годинника вважається стабільним, то його похибка у будь-який момент часу буде визначатися лише адитивною складовою від неправильного встановлення поточного часу в заданий момент часу. Тобто і за 1 год, і за 10 год похибка становитиме 
.
Задача 34. При вимірюванні температури за допомогою термоелектричного| перетворювача та мілівольтметра останній характеризується адитивною похибкою 
.
Знайти границі адитивної похибки вимірювання температури, якщо чутливість термоелектричного перетворювача приблизно становить 
.
Розв’язання. Граничне значення адитивної похибки вимірювання температури
=± 
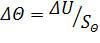Задача 35. Систематична мультиплікативна похибка цифрового омметра певного типу для заданих умов його роботи пронормована граничними значеннями 
від вимірюваного значення опору. Який зміст цього запису? Знайти границі абсолютної мультиплікативної похибки омметра.
Розв’язання. Цей запис означає, що для заданих умов роботи мультиплікативна складова похибки довільного цифрового омметра цього типу не вийде за границі 
від його показу 
.
Тобто границі абсолютної мультиплікативної похибки омметра
Задача 36. Знайти границі сумарної (адитивної та мультиплікативної) систематичної похибки цифрового омметра для умов прикладів 31 та 35.
Розв’язання. Границі сумарної похибки омметра дорівнюють сумі границь складових (адитивної та мультиплікативної) похибок, тобто
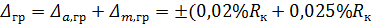
Задача 37. Нестабільність ходу годинника становить 
. У певний момент часу поточний час годинника встановлено практично без похибки. Яке значення набуде похибка від нестабільності ходу годинника через 12 год? через 12 діб?
Розв’язання. Оскільки час в початковий момент встановлено без похибки, то його похибка у будь-який момент часу буде визначатися лише мультиплікативною складовою від нестабільності ходу та пропорційна до значення поточного часу 
:
Тобто за 12 год
за 12 діб
Задача 38. Знайти границі сумарної (адитивної та мультиплікативної) систематичної похибки вимірювання часу годинником для умов задач 33 та 37 через 12 год від моменту калібрування годинника.
Розв’язання. Границі сумарної похибки дорівнюють сумі границь адитивної та мультиплікативної складових похибок годинника
тобто через 12год
Задача 39. Під час вимірювання температури за допомогою термоелектричного; перетворювача та мілівольтметра останній характеризується мультиплікативною похибкою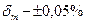 
. Знайти границі мультиплікативної похибки вимірювання температури, якщо чутливість термоелектричного перетворювача приблизно становить 
, вимірювана температура 
і напруга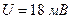 
.
Розв’язання. Значення мультиплікативної похибки вимірювання температури
тобто граничне значення цієї похибки
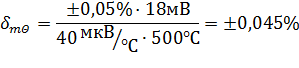
Практичне заняття №7
ІНСТРУМЕНТАЛЬНІ ПОХИБКИ
Теоретичні відомості
Інструментальні похибки - це похибки, що зумовлені недосконалістю засобів вимірювальної техніки та залежністю їх властивостей від впливу зовнішніх умов. Серед всіх інших можливих складових інструментальна похибка вимірювання є присутньою завжди, оскільки неможливе вимірювання без засобів (інструментів).
Засоби вимірювальної техніки використовують у певних умовах, серед них температура довкілля, його тиск, вологість, напруженість магнітного, електростатичного поля, інтенсивність електромагнітного поля, рівень завад спільного і нормального видів, рівень радіації, механічних вібрацій, стрясань та ударів, напруга та частота живлення, певне просторове положення та інші. Ці величини самі по собі можуть не бути вимірюваною величиною конкретного ЗВ, однак вони впливають на його роботу, змінюючи покази чи інші характеристики. їх називають виливними величинами.
Для кожної з величин встановлюють нормальні значення або область нормальних значень (нормальні умови), а також область робочих значень (робочі умови). Для кожного типу ЗВ регламентуються вид впливних величин і конкретні їх нормальні та робочі області значень.
Якщо всі регламентовані для цього ЗВТ впливні величини є в області нормальних значень (вважають, що вимірювання виконують в нормальних умовах), то для ЗВТ оцінюють лише основну похибку. Отже, основна похибка ЗВТ 
— це його похибка в нормальних умовах.
Якщо хоч одна з впливних величин виходить за межі нормальних значень, але є в межах робочих значень, то, крім основної, необхідно оцінювати додаткову похибку 
(7.1)
Для кожної виливної величини, значення якої вийшло за межі нормальної області (але є у межах робочої області), необхідно окремо оцінювати додаткові похибки. Тому в кожному конкретному випадку додаткових похибок може бути різна кількість.
Нарешті, якщо хоч одна з впливних величин виходить за межі робочої області, то інструментальна похибка не може бути оцінена і результати вимірювань не можна використовувати за призначенням.
Основну та додаткові похибки оцінюють згідно з нормативними документами (наприклад, паспортом чи технічними умовами) на відповідний ЗВТ, згідно з отриманими результатами та фактичними умовами вимірювання.
Часто ці похибки можна оцінити за класом точності ЗВТ
найчастіше відображає певним способом границі їх основної допустимої похибки, і здебільшого — зведеної.
За означенням зведена похибка ВП - це відношення абсолютної похибки до певного встановленого, так званого нормувального значення 
, як таке найчастіше використана кінцева 
(верхня) границя вимірювання цього діапазону (
).
(7.2)
Для аналогових (з покажчиком і шкалою) приладів клас точності переважно відображений одним числом, яке встановлює виражені у відсотках границі основної допустимої зведеної 
похибки
. (7.3)
У цьому виразі 
— границі основної абсолютної похибки. Якщо відомий клас точності та границі вимірювання, відповідно до означень можна визначити границі основних похибок
- Абсолютної 
, (7.4)
- Відносної 
. (7.5)
де 
— показ приладу.
Для цифрових приладів клас точності переважно відображений двома числами, що записані через косу риску: 
, зазвичай (
). Ці числа відображають виражені у відсотках границі основної зведеної похибки відповідно: 
— на початку (нульовий показ 
), та 
— у кінці границі вимірювання (показ 
):
; 
. (7.6)
Для проміжних показів (
) границі зведеної похибки приладу змінюються лінійно. Таке нормування зумовлено тим, що для цифрових приладів характерна як адитивна (незалежна від значення вимірюваної величини), так і мультиплікативна (що лінійно, прямо пропорційно залежить від значення вимірюваної величини) похибки.
Відповідно до означення зведеної похибки за класом точності (), показом 
та границею вимірювання в явному вигляді можна встановити границі похибок:
- абсолютної (рис. 10.2, а) — 
; (7.7)
- відносної (рис. 10.2, б) — 
. (7.8)
Отже, якщо клас точності цифрового приладу нормується у формі зведеної похибки двома числами, границі його основної абсолютної похибки лінійно зменшуються зі зменшенням показу (рис. 10.2, а). Границі відносної похибки, хоча зростають зі зменшенням показу (рис. 10.2, б), але не так швидко, як у аналогових приладах.
Тут також лише в кінці діапазону (показ приладу 
) границі відносної похибки числово збігаються з першим числом с у записі класу точності. Тобто загалом, не вживши якихось заходів, приладом класу точності неможливо виміряти величину з відносною похибкою, меншою за .
Порівняно з аналоговим амперметром границі відносної похибки цифрового амперметра при менших показах є істотно меншими (тут майже удвічі). Тобто, застосовуючи цифровий прилад, можна отримати вищу точність у ширших, межах зміни показу. Навіть на позначці в одну третю від кінця (
) границя відносної похибки при нормуванні класу точності двома числами збільшується від мінімального значення до значення
.
У зарубіжних цифрових приладах переважно нормують окремо адитивні (незалежні від значення вимірюваної величини) та мультиплікативні (пропорційні до значення вимірюваної величини) границі похибок. Часто адитивну границю виражають у відсотках (чи ррm) від діапазону вимірювання (of FS – of full scale), тобто у формі границь зведеної похибки
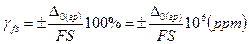, (7.9)
або в одиницях п молодшого розряду цифрового приладу (ОМР) – LSB (least significant bit — найменш значущий біт), тобто у формі границь абсолютної похибки,
. (7.10)
Очевидно, що між цими значеннями існує однозначний зв’язок і обома способами легко встановити границі абсолютної похибки
. (7.11)
де 
— кількість квантів у цілому діапазоні (кількість різних числових значень результату).
Мультиплікативні границі похибок, як правило, виражають у формі відносних похибок (у % чи ррт), тобто відносно значення вимірюваної величини чи показу приладу 
, (англ. of RE – of reading).
(7.12)
Як було зазначено вище, додаткові похибки оцінюють окремо для кожної впливної величини. Значення додаткових похибок виражають зазвичай у частках від основної, хоча спосіб оцінювання для різних впливних величин може бути дещо різним. Для одних впливних величин нормують функцію впливу (у вигляді графіка чи аналітичної залежності), яка встановлює значення додаткової похибки при виході значення впливної величини за межі нормальної області, для інших — коефіцієнт впливу- як відношення зміни показу до зміни впливної величини при виході її за межі нормальної області, можуть використовуватися інші способи, враховуючи особливості як впливних величин, так і самих ЗВ. Наприклад, для деяких цифрових приладів значення додаткової температурної похибки оцінюють в явному вигляді за виразом, подібним до виразу для оцінювання границь основної похибки
, (7.13)
де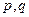 
— задані коефіцієнти з розмірністю 
; 
— відхилення температури від нормальної області.
Для переважної більшості аналогових, та багатьох цифрових, приладів додаткова температурна похибка встановлюється за коефіцієнтом впливу температури, який означений як відношення певної частини основної похибки до заданого відхиленім температури зовнішнього середовища. Зазвичай застосовують таке формулювання: додаткова температурна похибка не перевищує основної на кожні 10 °С (чи 5 °С, чи іншого) відхилення температури від нормальної області. Тут коефіцієнт впливу 
або 
(
— задана зміна температури) пов’язаний з границями основної похибки (для оцінювання абсолютної додаткової температурної похибки використовують границі основної абсолютної похибки 
, а для оцінювання відносної додаткової температурної похибки – границі основної відносної 
). Іноді вказують, що додаткова похибка не перевищує половини від основної, тоді при встановленому відхиленні температури коефіцієнт впливу удвічі менший.
За відомого відхилення температури 
від нормальної області границі додаткової температурної похибки оцінюють як добуток коефіцієнта впливу на це відхилення.
Для деяких впливних величин додаткову похибку нормують сталою у всій робочій області. Наприклад, у паспорті на прилад іноді вказується: якщо напруга живлення за межами нормальних значень 220 В ±4 %, але у межах від 186 В до 244 В додаткова похибка не перевищує половини (або цілої) основної. Тобто при довільній напрузі живлення приладу в межах від 186 В до 211,2 В, а також від 228,8 В до 244 В вважають, що границі додаткової похибки є однаковими і дорівнюють половині границь основної.
Подібно нормують границі додаткових, магнітної та інших похибок. У кожному конкретному випадку необхідно звернутися до паспорта на прилад і з’ясувати спосіб оцінювання як основної, так і додаткової похибок.
Загалом значення похибки на виході ЗВТ пропорційне до значення похибки на його вході, причому коефіцієнт пропорційності є крутістю (похідною) функції перетворення
. (7.14)
Отже, для того самого значення абсолютної похибки на вході ЗВТ значення абсолютної похибки на виході є більшим для таких значень вхідної величини, де більша крутість функції перетворення (чутливість ЗВТ).
Знаходження похибки на виході ЗВТ, якщо задана похибка на його вході, називають зведенням похибки до виходу, а саму похибку називають зведеною до виходу ЗВТ похибкою.
Якщо задана похибка на виході ЗВТ, абсолютна похибка на його вході є обернено пропорційною до крутості (похідної) функції перетворення
. (7.15)
Отже, тут навпаки, для того самого значення абсолютної похибки на виході значення абсолютної похибки на вході є більше для таких значень вхідної величини, де менша крутість функції перетворення (чутливість ЗВТ).
Знаходження похибки на вході ЗВТ, якщо задана похибка на його виході, називають зведенням похибки до входу, а саму похибку називають зведеною до входу ЗВТ похибкою.
Для ЗВТ з лінійною функцією перетворення (незалежно чи зі зміщенням, чи без нього) крутість (похідна) функції перетворення є сталою
(7.16)
і дорівнює коефіцієнту перетворення.Тому однаковим абсолютним похибкам на вході ЗВТ у всьому діапазоні значень вхідної величини відповідають однакові абсолютні похибки на виході ЗВТ
. (7.17)
Тобто якщо на вході 
, то на виході похибки теж однакові
. (7.18)
І навпаки, однаковим абсолютним похибкам на виході у всьому діапазоні значень величин відповідають однакові абсолютні похибки на вході ЗВТ.
. (7.19)
Тобто якщо на виході , то на вході ЗВТ також маємо рівність похибок (рис. 10.5, в)
. (7.20)
(7.21)
згідно з означенням відносна похибка на його виході описується виразом
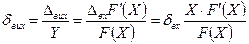. (7.22)
Тому, оскільки загалом для нелінійного ЗВТ
, (7.23)
то значення відносних похибок на вході і виході такого ЗВТ є різними
. (7.24)
Для лінійного ЗВТ з незміщеною відносно початку координат функцією перетворення, враховуючи (10.18), маємо
, (7.25)
тому після підстановки цього виразу у (10.23) відносні похибки дорівнюють одна одній
. (7.26)
Для лінійного ЗВТ із зміщеною відносно початку координат функцією перетворення (рис. 10.5, в) маємо
, (7.27)
тобто відносні похибки на вході і виході такого ЗВТ не дорівнюють одна одній.
Отже, лише для лінійного ЗВТ з незміщеною відносно початку координат функцією перетворення зведені до входу і виходу відносні похибки дорівнюють одна одній. Для лінійного ЗВТ із зміщеною щодо початку координат функцією перетворення і тим більше для нелінійного ЗВТ) зведені до входу і виходу відносні похибки відрізняються між собою.
Задача 40. Нехай для певного ЗВТ регламентовані такі нормальні умови: температура від 
до 
напруга живлення від 
до 
, з робоча область: температура від 
до 
і напруга живлення від 
до 
. Інші впливні величини для цього ЗВ не регламентовані. Цим ЗВТ в різний час було здійснено чотири вимірювання в різних умовах: 1) температура приміщення 
, напруга живлення —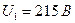 
; 2) 
, 
3) 
, 
; 4) 
, 
. Проаналізувати ці вимірювання відносно влливних величин.
Розв’язання. 1. Перше вимірювання виконано у нормальних умовах, бо і температура (
) і напруга живлення (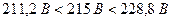
) знаходяться в області нормальних значень, тому оцінюють лише основну похибку ЗВ.
2.У другому вимірюванні температура є в межах нормальної області (
), а напруга живлення вийшла за межі нормальної області, але у межах робочої (), тому оцінюють основну та додаткову похибки від впливу зміни напруги живлення.
3.У третьому вимірюванні температура вийшла за межі нормальної області, але у межах робочої (
), а напруга живлення в межах нормальної області (
), тому оцінюють основну та додаткову температурні похибки.
4.У четвертому вимірюванні температура вийшла за межі нормальної області, але в межах робочої (
), а напруга живлення вийшла за межі робочої області (
), тому результат вимірювання є недостовірним і його не можна використати.
Задача 41. Амперметр на 
, класу точності 0,5. Встановити границі основної абсолютної похибки.
Розв’язання. Клас точності 0,5 означає, що границі основної (у нормальних умовах) допустимої зведеної (до ) похибки становлять ± 0,5%. Тому відповідно до (7.4)
незалежно від показу амперметра.
Задача 42. Для амперметра з прикладу 41 встановити границі основної відносної похибки, якщо показ амперметра 
.
Розв’язання. 1-й спосіб. Використати границі абсолютної похибки з прикладу 10.3. Згідно з означенням границі відносної похибки дорівнюють відношенню границь абсолютної похибки до показу, тому
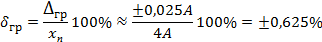
2-й спосіб. Безпосереднє застосування виразу (10.4), тобто
Отже, знайдені обома способами границі відносної похибки є однаковими.
Задача 43. Що означає клас точності 0,5/0,2 цифрового амперметра з границею вимірювання ?
Розв’язання Клас точності 0,5/0,2 означає, що границі основної (у нормальних умовах) допустимої зведеної (до ) похибки становлять: на початку діапазону (
) 
, і в кінці діапазону (
) 
.
Задача 44. Для згадуваного у прикладі 43 амперметра обчислити граничне значення відносної похибки, якщо показ дорівнює третині діапазону і порівняти з граничною відносною похибкою аналогового амперметра.
Розв’язання. 1. Якщо показ дорівнює третині діапазону (
), граничне значення відносної похибки дорівнює
2. При застосуванні аналогового амперметра 
, що дає для амперметра на 
граничне значення відносної похибки
або на 60 % більше.
Задача 45. Адитивні границі похибки трьох цифрових вольтметрів пронормовані і І такими значеннями: 1 – ± 0,02 %оf FS; 2 – ± 50 ррm оf FS; 3 – ± 5 LSB. Для першого приладу :границя вимірювання становить 1 V (
), для другого 10 V (
), а для третього 2 V (
), якщо кількість квантів у діапазоні 
. Визначити границі і, абсолютних похибок вольтметрів.
Розв’язання. 1. Відповідно до означень границі абсолютної адитивної похибки вольтметрів
першого — 
,
другого — 
,
третього — 
.
Задача 46. Мультиплікативні границі похибки згаданих вище цифрових вольтметрів пронормовані такими значеннями: 1) – 
; 2) – 
; 3) – 
. Покази приладів становили 
, для другого 
, 
. Визначити границі абсолютних похибок вольтметрів на вказаних показах.
Розв’язання. Відповідно до означення границі абсолютної мультиплікативної похибки вольтметрів
першого — 
,
другого —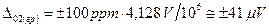 
,
третього — 
.
Задача 47. У документації на прилад записано, що нормальні умови щодо температури 
(від 
до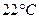 
), додаткова температурна похибка не перевищує основної на кожні 
(
) відхилення температури від нормальної області. Вимірювання виконувались при температурі в приміщенні, де знаходився прилад 
. Попередньо були оцінені границі основної відносної похибки 
. Оціните границі відносної додаткової температурної похибки.
Розв’язання. 1. Визначаємо відхилення температури від нормальної області
2. Обчислюємо границі (відносної) додаткової температурної похибки
Задача 48. Коефіцієнт підсилення вимірювального підсилювача становить 
. Діапазон вхідної напруги підсилювача становить 
, абсолютна похибка на вході підсилювача —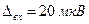 
. Знайти абсолютну похибку на виході підсилювача.
Розв’язання. Оскільки функція перетворення підсилювача є лінійною і проходить через початок координат
,
то згідно з (10.19) похибка на виході підсилювача становить
Задача 49. Напругу на виході подільника напруги 
виміряли з похибкою 5 мВ. Визначити абсолютну похибку на вході подільника напруги
Розв’язання. Оскільки функція перетворення подільника напруги є лінійною і проходить через початок координат
,
де 
— коефіцієнт перетворення подільника — величина, обернена до коефіцієнта ділення 
,
то згідно з (10.21) похибка на вході подільника напруги становить
|
Задача 50. Для умови прикладу 49 знайти відносну похибку підсилювача, якщо вхідна напруга дорівнює діапазону 
.
Розв’язання. Відносна похибка на вході підсилювача
Оскільки функція перетворення підсилювача є лінійною і проходить через початок координат, то відносні похибки на вході і виході підсилювача є однаковими, тобто
Задача 51. Для умови прикладу 50 знайти відносну похибку на вході подільника напруги, якщо виміряне значення вихідної напруги дорівнює діапазону 
.
Розв’язання. Відносна похибка напруги на виході подільника
Оскільки функція перетворення подільника напруги є лінійною і проходить через початок координат, то відносні похибки на вході і виході подільника є однаковими, тобто
Задача 52. Функція перетворення мідного терморезиетивного перетворювача (залежність вихідного опору 
від температури (вхідної) 
(
) описується виразом
·(I+α·Θ)
де 
— початковий опір при температурі 
, (наприклад, 
), 
— коефіцієнт відносної чутливості - відносної зміни опору зі зміною температури (наприклад, 
).
Значення вихідного опору перетворювача 
виміряли з похибкою, приблизне значення якої становить 
.
Оцінити абсолютну похибку вимірювання температури (звести похибку до входу перетворювача).
Розв’язання. Оскільки функція перетворення перетворювача є лінійною з крутістю (похідною)
то згідно з (10.17) зведена до входу абсолютна похибка
Задача 53. Для умови прикладу 52 знайти значення відносних похибок на виході та вході перетворювача і порівняти їх.
Розв’язання. Відносна похибка на виході перетворювача
Щоб визначити відносну похибку на вході, необхідно знайти значення вхідної величини-температури, яка відповідає виміряному значенню вихідної величини-опору.
Для цього необхідно скористатися виразом функції перетворення мідного терморезистивного перетворювача і знайти обернену функцію перетворення
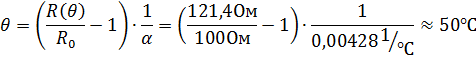
Тоді відносна похибка на вході перетворювача
Отже, відносні похибки на вході та виході перетворювача є різними.
Задача 54. Функція перетворення платинового терморезистивного перетворювача (залежність вихідного опору від температури (вхідної) () описується виразом
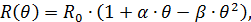
де — початковий опір при температурі 
, (наприклад, ), , 
— коефіцієнти залежності (наприклад, 
, 
).
Значення вихідного опору перетворювача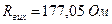 
виміряли з похибкою, приблизне значення якої становить 
.
Оцінити абсолютну похибку вимірювання температури (звести похибку до входу перетворювача).
Розв’язання. Оскільки функція перетворення перетворювача є нелінійною (параболічного), то, щоб знайти значення крутості (похідної)
,
необхідно знати значення температури, якій відповідає виміряне значення опору, використовуючи, наприклад, так звану градуювальну таблицю, в якій наведено відповідності між вхідною та вихідною величинами перетворювача або аналітичний вираз оберненої функції перетворення перетворювача - залежність вхідної величини від вихідної. Для параболічної функції перетворення обернена функція має вигляд
Тоді, підставляючи коефіцієнти функції перетворення та виміряне значення опору, знайдемо значення температури 
Далі розрахуємо значення крутості функції в точці
Тоді за виразом (7.17) знаходимо зведене до входу значення абсолютної похибки
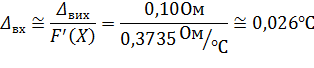
Задача 55. Для умови прикладу 54 знайти значення відносних похибок на виході та вході перетворювача і порівняти їх.
Розв’язання. Відносна похибка на виході перетворювача
Відносна похибка на вході перетворювача
Отже, тут також відносні похибки на вході та виході перетворювача є різними.
СПИСОК ЛІТЕРАТУРИ
1. Майстренко В.М., Морозова І.В., Осадчий В.П, Порєв В.А., Основи теорії засобів вимірювання: Монографія./Під аг.ред.Майстренка В.М. - Хмельницький, 2010
2. Орнатский П.П., Теоретические основы информационно-измерительной техники. – К.: “Вища школа”, 1983.
3. Поліщук Є.С., Дорожовець М.М., Яцук В.О. та ін. Метрологія та вимірювальна техніка: Підручник/ Є.С. Поліщук, М.М. Дорожовець, В.О. Яцук, В.М. Ванько, Т.Г. Бойко; За ред. проф. Є.С. Поліщука. – Львів: „Бескид Біт”, 2003. – 544 с.
4. Т.М. Алиев, А.А. Тер-Хачатуров. Измерительная техника. Учебное пособие для технических вузов. - М.: Высш. шк., 1991. – 382с.
5. Метрологическое обеспечение безопасности труда. Справочник под ред. И.Х. Сологяна. 2 тома. - М.: Изд. стандартов, 1989. – 490с.
6. Саранча Г.А., Якимчук Г.К. Метрологія, стандартизація та управління якістю: Підручник. – К.: Основа, 2004. – 376 с.
7. ГОСТ 12.0.005-84. ССБТ Метрологическое обеспечение в области безопасности труда. Основные положения.
8. ГОСТ 6636-69* (ст. СЭВ 514-77). Нормальные линейные размеры.
