Якщо відоме певне значення систематичної похибки, то її необхідно врахувати, ввівши поправку у результат (див. розділ 3 „Опрацювання результатів вимірювань”). Однак, забігаючи наперед, відзначимо, що неможливо точно знайти значення систематичної похибки, тобто неможливо повністю її виключити. Практично завжди виникають так звані невиключені залишки систематичної похибки, конкретні значення яких є невідомими. Тому тут і далі, коли йтиметься про характеристики систематичних похибок, мають на увазі їх значення після введення, якщо це можливо, поправок чи їх коригування.
Сталі систематичні похибки (невиключені залишки) зазвичай описують їх граничними значеннями, тобто такими значеннями, які може набувати похибка у найнесприятливіших умовах:
- Абсолютні
Δc=±Δгр або –Δгр≤Δс≤Δгр; (4.1)
- Відносні
δc=±δгр або –δгр≤δс≤δгр; (4.2)
Ці записи означають, що фактичне значення систематичної похибки залишається сталим, однак невідомим, не виходячи за встановлені граничні значення.
Систематичні похибки можуть бути функціями, наприклад, параметрів навколишнього середовища (температури, вологості, тиску, магнітного поля, напруги живлення тощо). Такі систематичні похибки розглядаються в наступних главах, зокрема у главі 10 „Інструмен-тальні похибки”.
Систематичні похибки також можуть бути функціями параметрів вимірювального кола, зокрема неінформативних (невимірюваних) параметрів об’єкта дослідження і можуть бути методичними. Наприклад, похибки від споживання приладами енергії від об’єкта вимірювання є систематичними. Такі похибки вже згадувалися в попередній главі і будуть аналізуватися у наступних.
Прогресуючі похибки
Прогресуючі похибки — це похибки, які практично лінійно змінюються в часі (зростають чи спадають), їх часто називають дрейфами (рис. 7.1, б). Вони зумовлені процесами старіння елементів засобів вимірювальної техніки, зокрема, порівняно короткотривалі прогресуючі похибки зумовлені розрядом елементів живлення. Насправді закон часової зміни похибки зазвичай є складнішим, часто експоненційним, однак для простоти описання протягом невеликих часових інтервалів приймають лінійне наближення часової зміни такої похибки.
Практично лінійно змінну в часі систематичну похибку зазвичай описують граничними значеннями, які вона може досягати за певний інтервал часу  :
:
- абсолютної
 (4.3)
(4.3)
- чи відносної
 (4.4)
(4.4)
Зокрема, можуть вказуватися абсолютні чи відносні граничні значення, які може досягати похибка за 1 год, 8 год, 24 год, 30 діб (1 міс), кілька місяців, рік, кілька років.
Задача 17. Абсолютна систематична похибка задана граничними значеннями  . Що означає цей запис?
. Що означає цей запис?
Розв’язання. Це означає, що залишаючись сталою і невідомою, абсолютна систематична похибка знаходиться в межах
-0,25мВ≤Δ≤+0,25 мВ
Під час повторних вимірювань ця похибка кожен раз буде набувати те саме значення із вказаного діапазону.
Задача 18. Граничне значення відносної систематичної похибки коефіцієнта підсилення підсилювача становить ± 0,02 %. Що означає цей запис?
Розв’язання. Це означає, що фактичне значення коефіцієнта підсилення конкретного значення коефіцієнта підсилення не більше ніж на 0,02 % в той чи інший бік. Тобто
К=Кп±0,02% Кп або Кп -0,02% Кп≤К≤ Кп +0,02% Кп
Задача 19. Абсолютна похибка вольтметра на  в режимі без калібрування може досягати значень
в режимі без калібрування може досягати значень  . Що означає цей запис? Знайти допустимі зміни похибки за півмісяця.
. Що означає цей запис? Знайти допустимі зміни похибки за півмісяця.
Разв’язання. Це означає, то похибка вольтметра після останнього калібрування за один місяць в найгіршому випадку не перевищить значення  в той чи інший бік.
в той чи інший бік.
За півмісяця слід очікувати систематичну похибку, не більшу за половину граничною значення, тобто за  і т.д.
і т.д.
Задача 20. Відносна часова нестабільність резистора задана граничним значенням 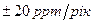 .
.
Що означає цей запис? Яка можлива максимальна зміна опору резистора за 5 років?
Розв’язання. Це означає, що за один рік експлуатації резистора його опір може змінитися не більше ніж на  в той чи інший бік.
в той чи інший бік.
А за п’ять років експлуатації ця зміна в найгіршому випадку може досягати у п’ять разів більшого значення, тобто  .
.
Важливим є те, що фактична зміна опору конкретного резистора без виконання додаткових досліджень залишається невідомою, однак обмеженою граничними значеннями.
Практичне заняття №5
ВИПАДКОВІ ПОХИБКИ
Теоретичні відомості
Випадкові похибки - це похибки, що змінюються в часі нерегулярно, не передбачувано, а їх майбутні значення можна прогнозувати лише з певною часткою ймовірності. Результати вимірювань, спотворені випадковими похибками, змінюються хаотично. На практиці буває важко відразу відрізнити випадкову похибку віл змінної регулярної, наприклад, періодичної.
Функція розподілу є інтегральною характеристикою густини розподілу
 (5.1)
(5.1)
Вона є додатною (як ймовірність), неспадною функцією, що змінює своє значення від 0до 1.
Знаючи функцію розподілу, можна відразу, оминаючи густину розподілу, знайти ймовірність появи похибки в інтервалі 
 (5.2)
(5.2)
Очевидно, що знаючи функцію розподілу випадкової похибки, диференціюючи її, легко розрахувати густину розподілу
 (5.3)
(5.3)
Для стандартного нормального розподілу ( і
і  ) функція розподілу
) функція розподілу
 (5.4)
(5.4)
Для нормального розподілу, крім такого означення, зустрічаються також дещо інші означення функції розподілу. Зокрема, часто наводять таблиці значень функції розподілу при нульовому початковому значенні похибки, а не для  :
:
 (5.5)
(5.5)
Оскільки для стандартного нормального розподілу 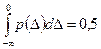 , то вирази (5.4) і (5.5) однозначно пов'язані між собою
, то вирази (5.4) і (5.5) однозначно пов'язані між собою
 (5.6)
(5.6)
Оскільки густина розподілу для великих за модулем значень похибки зменшується, то ймовірність появи таких похибок також зменшується. Основна частина значень похибок групується у порівняно невеликих межах. Під час експериментальних досліджень важливо мати впевненість, що випадкова похибка не виходить за певні межі або що поява похибок, більших за допустимі значення, у цьому експерименті є малоймовірною. Ця проблема вирішується застосуванням такої інтервальної характеристики випадкової похибки, як її довірчі границі. Вони утворюють інтервал, в якому в середньому знаходиться частка 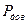 всіх можливих значень випадкової похибки, де
всіх можливих значень випадкової похибки, де 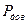 — довірча ймовірність, її ще іноді називають вірогідністю (тоді границі називають вірогідними). Довірчі границі — нижню
— довірча ймовірність, її ще іноді називають вірогідністю (тоді границі називають вірогідними). Довірчі границі — нижню  і верхню
і верхню  теоретично розраховують як значення похибок, за яких функція розподілу похибки досягає симетричних значень (рис. 4, а):
теоретично розраховують як значення похибок, за яких функція розподілу похибки досягає симетричних значень (рис. 4, а):
знизу 
і зверху  , (5.7)
, (5.7)
де  — ймовірність (ризик) виходу похибки за межі довірчих границь
— ймовірність (ризик) виходу похибки за межі довірчих границь
(рис. 4, б).
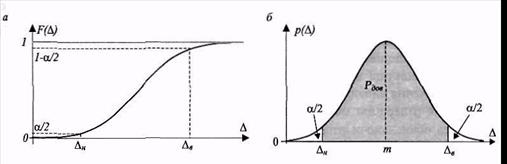
Рис.4 Довірчі границі випадкової похибки
Для симетричних відносно середини розподілів довірчі границі також симетричні. Зокрема, для симетричного щодо нуля розподілу  .
.
У вимірювальній практиці прийнято такі типові значення довірчої ймовірності  ,
,  ,
,  ,
,  , для яких ймовірність а виходу випадкової похибки за довірчі границі становить відповідно 0,1; 0,05; 0,01 та 0,0027.
, для яких ймовірність а виходу випадкової похибки за довірчі границі становить відповідно 0,1; 0,05; 0,01 та 0,0027.
У разі стандартного нормального розподілу (якщо  і
і  ) довірчі границі для різних довірчих ймовірностей набувають значення
) довірчі границі для різних довірчих ймовірностей набувають значення
 : |Δ дов |≈ 1,65=z(0,90)
: |Δ дов |≈ 1,65=z(0,90)
 : |Δ дов |≈ 1,96=z(0,95)
: |Δ дов |≈ 1,96=z(0,95)
 : |Δ дов |≈ 2,58=z(0,99)
: |Δ дов |≈ 2,58=z(0,99)
 : |Δ дов |≈ 3=z(0,9973) (5.8)
: |Δ дов |≈ 3=z(0,9973) (5.8)
де  — коефіцієнт, що називається квантилем стандартного нормального розподілу, який визначає границі, в межах яких знаходиться
— коефіцієнт, що називається квантилем стандартного нормального розподілу, який визначає границі, в межах яких знаходиться 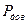 частка похибок.
частка похибок.
Аналізуючи (8.13), можемо дійти висновку, що в середньому 95 % нормально розподілених похибок знаходяться в межах  ; і лише в середньому 5 % похибок виходять за ці межі, далі в середньому 99 % значень похибки лежать в межах
; і лише в середньому 5 % похибок виходять за ці межі, далі в середньому 99 % значень похибки лежать в межах  (в середньому 1 % — за цими межами), і нарешті, в середньому 99,73 % лежать у межах
(в середньому 1 % — за цими межами), і нарешті, в середньому 99,73 % лежать у межах 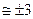 (і лише в середньому 0,27 % — за цими межами). Поява похибок з відхиленням понад
(і лише в середньому 0,27 % — за цими межами). Поява похибок з відхиленням понад  є малоймовірною подією.
є малоймовірною подією.
математичне сподівання  характеризує серединне значення, навколо якого групуються можливі значення похибки (рис. 8.5, а). Його практичною оцінкою є середнє значення випадкової похибки. Під час теоретичного аналізу математичне сподівання (операцію математичного сподівання позначають символом
характеризує серединне значення, навколо якого групуються можливі значення похибки (рис. 8.5, а). Його практичною оцінкою є середнє значення випадкової похибки. Під час теоретичного аналізу математичне сподівання (операцію математичного сподівання позначають символом  ) знаходять, обчислюючи інтеграл від добутку похибки на її густину розподілу
) знаходять, обчислюючи інтеграл від добутку похибки на її густину розподілу
 (5.9)
(5.9)
Для рівномірного у межах від  до
до  розподілу похибки математичне сподівання можна знайти без обчислення інтеграла як середину прямокутника
розподілу похибки математичне сподівання можна знайти без обчислення інтеграла як середину прямокутника
 (5.10)
(5.10)
При нормальному розподілі параметр  якраз і є математичним сподіванням. Розмірність математичного сподівання дорівнює розмірності похибки.
якраз і є математичним сподіванням. Розмірність математичного сподівання дорівнює розмірності похибки.
Мірою тісноти групування значень похибки навколо математичного сподівання чи мірою розсіювання випадкової похибки є її дисперсія. Дисперсію при теоретичному аналізі знаходять як математичне сподівання квадрата відхилення похибки від її математичного сподівання, тобто обчислюємо інтеграл
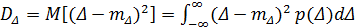 (5.11)
(5.11)
Чим більше розсіяння похибки, тим більша її дисперсія. Власне слово „дисперсія” і означає розсіяння. Розмірність дисперсії дорівнює квадрату розмірності похибки.
Підносячи до квадрата підінтегральний вираз, для розрахунку дисперсії можемо використовувати інший, часто простіший, шлях
 (5.12)
(5.12)
Тобто дисперсія похибки — це різниця між: математичним сподіванням квадрата похибки та квадратом її математичного сподівання.
Для рівномірно розподіленої похибки дисперсія становить одну дванадцяту від квадрата розмаху
 (5.13)
(5.13)
Додатний квадратний корінь з дисперсії похибки називається стандартним відхиленням, або середнім квадратичним значенням похибки
 (5.14)
(5.14)
Її розмірність збігається з розмірністю похибки, а, отже, і вимірюваної величини. Для нормально розподіленої похибки, як вже було сказано, власне другий параметр розподілу  —є стандартним відхиленням, або середньоквадратичним значенням.
—є стандартним відхиленням, або середньоквадратичним значенням.
За відомого стандартного відхилення, підносячи його до квадрата, легко розрахувати дисперсію похибки
 (5.15)
(5.15)
У загальному випадку для нормального розподілу з ненульовим центром розподілу ( ) та відмінним від одиниці стандартним відхиленням (
) та відмінним від одиниці стандартним відхиленням ( ) довірчі границі похибки при заданій довірчій ймовірності знаходять з використанням вказаних значень і відповідного квантилю стандартного нормального розподілу за виразом
) довірчі границі похибки при заданій довірчій ймовірності знаходять з використанням вказаних значень і відповідного квантилю стандартного нормального розподілу за виразом
 і
і 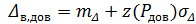 (5.16)
(5.16)
або сумісно
 (5.17)
(5.17)
Для інших розподілів випадкових похибок існують свої квантилі  та
та  , і довірчі границі можуть бути розраховані за подібними виразами
, і довірчі границі можуть бути розраховані за подібними виразами
 і
і  (5.18)
(5.18)
Опрацьовуючи результати вимірювань, що містять випадкову похибку, і після встановлення довірчих границь ми не маємо твердої гарантії, що конкретне значення похибки не вийде за ці границі. Ми лише маємо впевненість, що при повторних вимірюваннях на велику групу результатів (наприклад,  чи більше) в середньому може припасти лише невелика частка
чи більше) в середньому може припасти лише невелика частка  результатів з випадковими похибками, що вийшли за довірчі границі. Більше того, якщо зробити декілька серій, наприклад, по
результатів з випадковими похибками, що вийшли за довірчі границі. Більше того, якщо зробити декілька серій, наприклад, по  вимірювань, то в окремих серіях кількість виходів похибки за довірчі границі може відрізнятися від середнього значення як в один, так і в інший бік. Зокрема, при
вимірювань, то в окремих серіях кількість виходів похибки за довірчі границі може відрізнятися від середнього значення як в один, так і в інший бік. Зокрема, при  в середньому 5 результатів зі 100 може вийти за довірчі границі, однак у послідовних серіях вимірювань можна отримати кількість виходів за довірчі границі 3,7,0,2,4,5 тощо.
в середньому 5 результатів зі 100 може вийти за довірчі границі, однак у послідовних серіях вимірювань можна отримати кількість виходів за довірчі границі 3,7,0,2,4,5 тощо.
Якщо маємо декілька випадкових похибок  з математичними сподіваннями
з математичними сподіваннями  та дисперсіями
та дисперсіями  то у теорії випадкових похибок доведено, що математичне сподівання має такі властивості:
то у теорії випадкових похибок доведено, що математичне сподівання має такі властивості:
- математичне сподівання алгебраїчної суми як незалежних, так і залежних випадкових похибок дорівнює алгебраїчній сумі їх математичних сподівань:
 (5.19)
(5.19)
- математичне сподівання добутку невипадкової величини  на випадкову похибку
на випадкову похибку  дорівнює добутку цієї величини на математичне сподівання
дорівнює добутку цієї величини на математичне сподівання  випадкової похибки:
випадкової похибки:
 (5.20)
(5.20)
Дисперсія незалежних випадкових величин має дещо інші властивості:
- дисперсія алгебраїчної суми незалежних випадкових величин дорівнює сумі їх дисперсій (звернути увагу - просто сумі, а не алгебраїчній):
 (5.21)
(5.21)
- дисперсія добутку невипадкової величини С на випадкову дорівнює добутку квадрата цієї величини на дисперсію 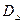 , похибки
, похибки
 (5.22)
(5.22)
Для нормально розподілених похибок їх сума завжди має нормальний розподіл (стійкість нормального розподілу), тому, знайшовши математичне сподівання і стандартне відхилення (дисперсію) сумарної похибки, відразу можемо визначити довірчі границі цієї похибки за виразом
 (5.23)
(5.23)
Оскільки згідно із законом великої кількості вже для 5-6 складових похибки розподіл їх алгебраїчної суми стає достатньо близьким до нормального, то, використовуючи зазначені властивості числових характеристик (математичного сподівання та дисперсії суми похибок), можемо оцінити довірчі границі сумарної похибки за (8.33).
Зокрема, для рівномірно розподілених у симетричних межах  випадкових похибок з ваговими коефіцієнтами С у виразі сумарної похибки
випадкових похибок з ваговими коефіцієнтами С у виразі сумарної похибки
 (5.24)
(5.24)
довірчі границі сумарної похибки при довірчій ймовірності 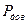 можна оцінити так. Спочатку необхідно розрахувати математичне сподівання та стандартне відхилення (середньоквадратичне) значення сумарної похибки, і далі визначити відповідний квантиль нормального розподілу сумарної похибки.
можна оцінити так. Спочатку необхідно розрахувати математичне сподівання та стандартне відхилення (середньоквадратичне) значення сумарної похибки, і далі визначити відповідний квантиль нормального розподілу сумарної похибки.
Для рівномірно розподілених похибок їх математичні сподівання збігаються з серединами розподілу. Оскільки за умовою всі складові розподілені в симетричних відносно нуля межах ( ), то їх математичні сподівання дорівнюють нулеві:
), то їх математичні сподівання дорівнюють нулеві:  .
.
Розмах кожного розподілу становить подвійне граничне значення похибки
 . Тому дисперсія кожної складової похибки
. Тому дисперсія кожної складової похибки
 (5.25)
(5.25)
Використовуючи властивості математичного сподівання і дисперсії алгебраїчної суми та масштабування похибок, знайдемо:
- математичне сподівання сумарної похибки

 (5.26)
(5.26)
- дисперсію сумарної похибки
 (5.27)
(5.27)
Стандартне відхилення (середньоквадратичне значення) сумарної похибки знайдемо як корінь з дисперсії
 (5.28)
(5.28)
Для розрахунку квантилів необхідно було б знайти розподіл алгебраїчної суми промасштабованих похибок, тобто обчислити згортку чотирьох відповідних рівномірних розподілів. Однак, використовуючи властивість розподілу суми декількох випадкових похибок, а саме, враховуючи, що вже при чотирьох приблизно рівноважних похибках розподіл їх суми дуже близький до нормального, для заданої 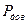 знаходять квантилі нормального розподілу
знаходять квантилі нормального розподілу  і довірчі границі сумарної похибки записують як
і довірчі границі сумарної похибки записують як
 (5.29)
(5.29)
Отже, використовуючи числові характеристики випадкових похибок, а також інші їх властивості, легко розрахувати довірчі границі алгебраїчної суми декількох складових, оминаючи пряме знаходження густини розподілу сумарної похибки. В цьому власне і полягає доцільність застосування числових характеристик, крім того, як буде показано нижче, числові характеристики випадкових похибок піддаються простому експериментальному визначенню, на відміну від їх густини розподілу
Очевидно, що такий шлях оцінювання довірчих границь значно простіший, ніж попередньо розраховувати згортку.
Статистичний (імовірнісний) зв’язок між двома похибками  та
та 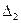 , прийнято характеризувати кореляційним
, прийнято характеризувати кореляційним  та коваріаційним
та коваріаційним  моментами як математичним сподіванням в першому випадку добутку похибок, а в другому — їх центрованих значень
моментами як математичним сподіванням в першому випадку добутку похибок, а в другому — їх центрованих значень

 (5.30)
(5.30)
 (5.31)
(5.31)
Обидва моменти є симетричними відносно обох похибок, тобто  ;
;  . Вони однозначно пов’язані між собою
. Вони однозначно пов’язані між собою
 (5.32)
(5.32)
Згідно з означеннями обидва моменти характеризують лише лінійний статистичний зв’язок між похибками, а не зв’язок взагалі. Якщо як друга похибка виступає та сама ( ), то
), то
 (5.33)
(5.33)
Коефіцієнт кореляції між похибками. Коваріаційний момент між двома похибками може набувати довільні значення, у цьому відношенні зручнішим та інформативнішим є так званий коефіцієнт кореляції як нормований до добутку стандартних відхилень обох похибок коваріаційний момент
 =
=  (5.34)
(5.34)
Коефіцієнт кореляції може набувати значення в діапазоні  .
.
Додатне значення коефіцієнта кореляції означає, що збільшення однієї похибки супроводжується зростанням іншої, від’ємний коефіцієнт — відображає факт зменшення однієї зі зростанням іншої похибки. Тут мають на увазі не буквальний функціональний зв’язок між похибками, а статистичний, що відображає тенденцію залежностей похибок. Якщо коефіцієнт кореляції додатний із загальною тенденцією до збільшення, для конкретних пар похибок можна спостерігати зворотне — зменшення.
Якщо коефіцієнт кореляції дорівнює нулеві (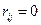 ), то говорять, що похибки є некорельованими. На практиці некорельованими вважають похибки, якщо коефіцієнт кореляції за модулем не перевищує певного невеликого значення
), то говорять, що похибки є некорельованими. На практиці некорельованими вважають похибки, якщо коефіцієнт кореляції за модулем не перевищує певного невеликого значення  . Часто приймають
. Часто приймають  . Навпаки, якщо модуль коефіцієнта кореляції більший за значення 0,7...0,8, то говорять про тісно корельовані похибки.
. Навпаки, якщо модуль коефіцієнта кореляції більший за значення 0,7...0,8, то говорять про тісно корельовані похибки.
Урахування коефіцієнта кореляції необхідне для правильного обчислення характеристик сукупності похибок, зокрема, їх дисперсії. Дисперсія суми двох корельованих похибок визначається так

тобто
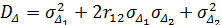 (5.35)
(5.35)
Якщо похибки некорельовані ( ), то дисперсія суми похибок дорівнює сумі дисперсій
), то дисперсія суми похибок дорівнює сумі дисперсій
 (5.36)
(5.36)
якщо ж похибки 100 % додатно корельовані ( ), то дисперсія квадрата суми стандартних відхилень
), то дисперсія квадрата суми стандартних відхилень
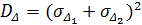 (5.37)
(5.37)
а при 100 % від’ємній кореляції ( ) дисперсія дорівнює квадрату різниць стандартних відхилень
) дисперсія дорівнює квадрату різниць стандартних відхилень
 (5.38)
(5.38)
Отже, неврахування кореляційних зв’язків між похибками може спричинити отримання неправильного значення дисперсії і пов'язаних з нею інших характеристик сумарної похибки (наприклад, довірчого інтервалу).
Усі можливі значення коваріантного моменту двох похибок утворюють так звану дисперсійну, а точніше, коваріаційну матрицю двох похибок
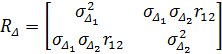 (5.39)
(5.39)
Вона є квадратною і симетричною відносно головної діагоналі, на якій знаходяться дисперсії похибок. Якщо вони для обох похибок однакові, тобто  , то ця матриця набуває вигляд
, то ця матриця набуває вигляд
 (5.40)
(5.40)
Коваріаційна матриця сукупності декількох похибок. Основною характеристикою сукупності п похибок вимірювань, подібно як і двох, є їх коваріаційна матриця
 (5.41)
(5.41)
яка є симетричною, її діагональні члени є дисперсіями випадкових похибок  , а бокові члени визначаються попарними коефіцієнтами кореляції
, а бокові члени визначаються попарними коефіцієнтами кореляції  між
між 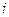 -ю та
-ю та  -ю похибками.
-ю похибками.
Задача 21. Випадкова похибка має рівномірний розподіл у межах від –5 мВ до +25 мВ. Визначити математичне сподівання похибки і записати розподіл похибки.
Розв’язання, 1. Математичне сподівання похибки становить
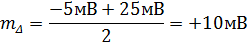
2. Висота прямокутника рівномірного розподілу обернена до розмаху розподілу

тому розподіл похибки

Задача 22. Випадкова похибка, як у задачі 21, має рівномірний розподіл у межах від -5 мВ до +25 мВ. Визначити дисперсію та стандартне відхилення похибки.
Розв’язання. 1. Дисперсія похибки становить
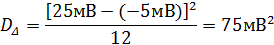
2. Стандартне відхилення дорівнює

Густина нормального (гауссівського) розподілу (рис. 3, в) має характерну дзвоно-подібну форму. За такої форми розподілу при повторних вимірюваннях менші за модулем похибки слід очікувати значно частіше ніж більші. Поява додатних та від’ємних похибок рівноможлива. У практику такий розподіл ввів Гаусс, тому його називають ще й гауссівським. Особливістю нормального розподілу є його стійкість, що проявляється двояко.
Перше — алгебраїчна сума довільної кількості випадкових похибок, кожна з яких розподілена за нормальним законом, завжди має нормальний розподіл.
Друге — не менш важливе, розподіл алгебраїчної суми великої кількості випадкових похибок з різними розподілами прямує до нормального (так званий закон великої кількості). Більше того, якщо серед похибок немає таких, що явно домінують над іншими, тобто вони приблизно є рівноважними, то вже при 5 – 6 складових розподіл їх алгебраїчної суми настільки близький до нормального, що для багатьох практичних застосувань фактичний розподіл приймається як нормальний.
Аналітично нормальний розподіл описується виразом
 =
= 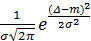 ,
,  (5.42)
(5.42)
тут  і
і  —параметри розподілу.
—параметри розподілу.
Перший з них ( ) характеризує серединне значення, навколо якого групуються можливі значення похибки (у такому разі він називається математичним сподіванням похибки). Другий — (
) характеризує серединне значення, навколо якого групуються можливі значення похибки (у такому разі він називається математичним сподіванням похибки). Другий — ( ) характеризує ширину розсіяння значень похибки навколо серединного значення (у такому разі його називають стандартним відхиленням або, що не зовсім правильно, середньоквадратичним відхиленням). Зі збільшенням
) характеризує ширину розсіяння значень похибки навколо серединного значення (у такому разі його називають стандартним відхиленням або, що не зовсім правильно, середньоквадратичним відхиленням). Зі збільшенням  густина розподілу стає сплющеною до горизонтальної осі (більше розсіяння похибок), а при зменшенні
густина розподілу стає сплющеною до горизонтальної осі (більше розсіяння похибок), а при зменшенні  вона витягується у вертикальному напрямку (менше розсіяння похибок). Значення густини так званого стандартного нормального розподілу (
вона витягується у вертикальному напрямку (менше розсіяння похибок). Значення густини так званого стандартного нормального розподілу ( і
і  ) можна знайти у всій довідковій літературі з теорії ймовірності.
) можна знайти у всій довідковій літературі з теорії ймовірності.
Для стандартного нормального розподілу ( і
і  ) функція розподілу (рис. 3, г)
) функція розподілу (рис. 3, г)
 (5.43)
(5.43)
Задача 23. Випадкова похибка має нормальний розподіл з параметрами  ,
, 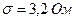 . Визначити її математичне сподівання, стандартне відхилення і дисперсію, записати розподіл похибки.
. Визначити її математичне сподівання, стандартне відхилення і дисперсію, записати розподіл похибки.
Розв'язання. 1. Відповідно до означення параметр т нормального розподілу є математичним сподіванням похибки, тому

2. Відповідно до означення параметр ст нормального розподілу є стандартним відхиленням похибки

3. Дисперсія похибки дорівнює квадрату стандартного відхилення, тобто

4.Відповідно до (8.53)  =
= 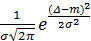 ,
,  вираз густини розподілу
вираз густини розподілу  =
=  ,
, 
Задача 24. Випадкова похибка має рівномірний розподіл у межах від  до
до  . Визначити довірчі границі похибки для довірчої ймовірності
. Визначити довірчі границі похибки для довірчої ймовірності 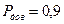 .
.
Розв’язання. 1. Математичне сподівання похибки є нульовим
(-0,3 мТл+ 0,3 мТл)/2=0 мТл
тобто розподіл є симетричним відносно початку координат.
2. Тому для такого рівномірного розподілу відношення довірчої границі  до граничного значення
до граничного значення  безпосередньо дорівнює довірчій ймовірності
безпосередньо дорівнює довірчій ймовірності

Звідси для  та
та  знаходимо довірчі границі
знаходимо довірчі границі  :
:

 =0,9·0,3 мТл
=0,9·0,3 мТл
Задача 25. Випадкова похибка має нормальний розподіл з параметрами  ,
,  . Визначити довірчі границі похибки для
. Визначити довірчі границі похибки для 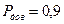 та
та  .
.
Розв’язання.
1.Відповідно до означення параметри т та а нормального розподілу є математичним сподіванням та стандартним відхиленням похибки, тому

2.Відповідно до (5.8)
 : |Δ дов |≈ 1,65=z(0,90)
: |Δ дов |≈ 1,65=z(0,90)
 : |Δ дов |≈ 1,96=z(0,95)
: |Δ дов |≈ 1,96=z(0,95)
 : |Δ дов |≈ 2,58=z(0,99)
: |Δ дов |≈ 2,58=z(0,99)
 : |Δ дов |≈ 3=z(0,9973)
: |Δ дов |≈ 3=z(0,9973)
для заданих довірчих ймовірностей квантилі становлять відповідно:
z(0,90)=1,65, z(0,95)=1,96, z(0,99)=2,58
3.Відповідні довірчі границі похибки знайдемо за виразом (5.17)




Задача 26. Відомі параметри нормального розподілу трьох складових похибки вимірювання опору:

Знайти математичне сподівання, дисперсію та стандартне відхилення сумарної похибки.
Розв’язання. 1. Математичне сподівання сумарної похибки дорівнює алгебраїчній сумі математичних сподівань складових

2. Дисперсія суми незалежних похибок дорівнює сумі їх дисперсій, а останні для нормального розподілу дорівнюють квадрату стандартного відхилення, тому

4. Стандартне відхилення сумарної похибки дорівнює квадратному кореню з дисперсії
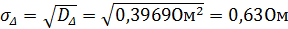
Задача 27. Для умови і розв’язків задачі 26 знайти довірчі границі похибки для  .
.
Розв’язання 1. Для  квантиль нормального розподілу
квантиль нормального розподілу  .
.
2. Підставляючи отримане в прикладі 8.6 значення стандартного відхилення сумарної похибки у (8.33)  , матимемо довірчі границі сумарної похибки
, матимемо довірчі границі сумарної похибки
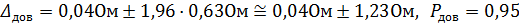
Задача 28. Відомі граничні значення незалежних рівномірно розподілених похибок




Знайти математичне сподівання, дисперсію та стандартне відхилення сумарної похибки.
Роїв 'язання, 1. Оскільки похибки задані лише своїм граничним значенням, то їх розподіл є симетричним відносно початку координат, тобто їх математичні сподівання є нульовими

Отже, математичне сподівання сумарної похибки також дорівнює нулеві.
2. Дисперсія суми незалежних похибок дорівнює сумі іх дисперсій, а останні для
рівномірного розподілу дорівнюють одній третій квадрата граничного значення, тому

4.Стандарте відхиленнясумарної похибки дорівнює квадратному кореню з дисперсії
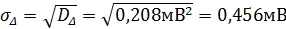
Задача 29. Для умови і розв’язків задачі 28 знайти довірчі границі похибки для  .
.
Розв'язання, 1. Для  квантиль нормального розподілу
квантиль нормального розподілу  .
.
2. Підставляючи отримане в задачі 28 значення стандартного відхилення сумарної похибки у (8.39)
 , матимемо довірчі границі сумарної похибки
, матимемо довірчі границі сумарної похибки 

Задача 30. Три нормально розподілені випадкові похибки з нульовим математичним сподіванням та стандартними відхиленнями:

є статистично залежними, характеризуються взаємними коефіцієнтами кореляції



Знайти дисперсію та стандартне відхилення сумарної похибки і порівняти їх із значеннями, отриманими без урахування взаємної кореляції.
Розв’язання. 1. Використовуючи (8.45) для трьох складових похибки, визначимо дисперсію сумарної похибки
 +
+ 
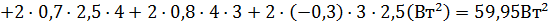
2. Стандартне відхилення сумарної похибки

3. Дисперсія сумарної похибки без урахування кореляції похибок

4. Стандартне відхилення сумарної похибки без урахування кореляції похибок
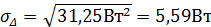
5. Отже, неврахування взаємної кореляції похибок призводить до того, що отримані таким способом дисперсія та стандартне відхилення сумарної похибки істотно відрізняються від їх справжніх значень.
Практичне заняття №6






