Определение точки разрыва
Точка 
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
1. функция 
определена в точке и ее окрестности;
2. существует конечный предел функции в точке ;
3. это предел равен значению функции в точке , т.е. 
Точка разрыва первого рода
Если в точке существуют конечные пределы 
и 
, такие, что 
, то точка называется точкой разрыва первого рода.
Точка разрыва второго рода
Если хотя б один из пределов или не существует или равен бесконечности, то точка называется точкой разрыва второго рода.
Точка устранимого разрыва
Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции в точке : 
или функция не определена в точке , то точка называется точкой устранимого разрыва.
11.Производная функции, её геометрический и механический смысл.
Производная. Рассмотрим некоторую функцию y = f (x) в двух точках x 0 и x 0 +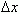 
: f (x 0) и f (x 0 + 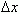). Здесь через 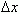обозначено некотороемалое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f (x 0 + 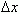) - f (x 0)называется приращением функции. Производной функции y = f (x) в точке x 0называется предел:
Если этот предел существует, то функция f (x) называется дифференцируемой в точке x 0. Производная функции f (x) обозначается так:
Геометрический смысл производной. Рассмотрим график функции y = f (x):
Из рис.1 видно, что для любых двух точек A и B графика функции:
где 
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то 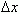неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Уравнение касательной. Выведем уравнение касательной к графику функции в точке A (x 0, f (x 0)). В общем случае уравнение прямой с угловым коэффициентом f ’(x 0) имеет вид:
y = f ’(x 0) · x + b.
Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:
f (x 0) = f ’(x 0) · x 0 + b,
отсюда, b = f (x 0) – f ’(x 0) · x 0, и подставляя это выражение вместо b, мы получим уравнение касательной:
y = f (x 0) + f ’(x 0) · (x – x 0).
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t 0 до t 0 + 
точка перемещается на расстояние: x (t 0 + ) - x (t 0) = 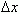, а её средняя скорость равна: va = 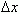/ . При 
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:
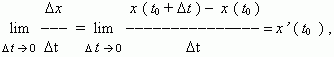
отсюда, v (t 0) = x’ (t 0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t).
12. Основные правила дифференцирования.
Операция дифференцирования или нахождения производной функции обладает фундаментальным свойством линейности. Это свойство упрощает нахождение производных функций, которые образованы из основных элементарных функций с помощью операций сложения и умножения на постоянное число. Простейшие правила дифференцирования позволяют вычислять производные таких функций без использования формального определения производной. Рассмотрим эти правила более подробно.
Производная постоянной величины.
Если f(x)=C, тоf′(x)=C′=0.Доказательство этого правила рассмотрено на странице Определение производной.
