Рассмотрим стационарное течение вязкой несжимаемой жидкости между двумя параллельными пластинам. Пластины находятся на расстоянии y ± а от оси O x, вдоль которой течет жидкость под действием перепада давления вдоль этой оси. В отличие от плоского течения Пуазейля, в направлении, перпендикулярном пластине, приложено внешнее магнитное поле B, а жидкость считаем электропроводной. Все параметры, как и в течении Пуазейля, являются функциями только координаты y (кроме давления, градиент которого вдоль оси O x создает течение жидкости). В этом случае уравнение неразрывности div V= 0 удовлетворяется тождественно, а из уравнения div B = 0 следует
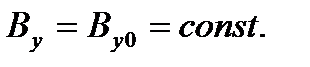
Проекция уравнения движения на ось O x дает
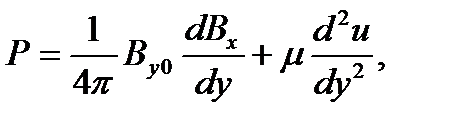
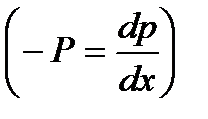(2)
где последний член представляет собой силы вязкости. Поскольку левая часть уравнения (2) есть функция только координаты x, а правая зависит только от координаты y, то Р =const. Проекция уравнения индукции магнитного поля (1) приводит к уравнению
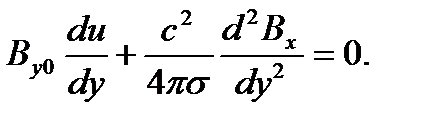(3)
Систему уравнений (2) и (3) будем решать при обычных граничных условиях прилипания для скорости и равенства нулю индуцированной x – компоненты магнитного поля
u = 0, B x= 0 при у = ± a. (4)
Решением уравнений (2) и (3) при граничных условиях (4) будет
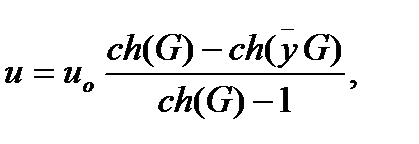
(5)
Здесь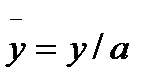 
, 
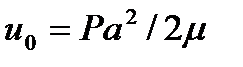– максимальная скорость жидкости на оси симметрии, а G - число Гартмана, определяющее порядок отношения электромагнитной силы к вязкой и определяется формулой
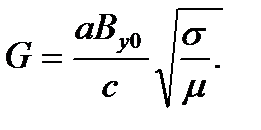
Это выражение легко получить, оценивая отношение этих сил по порядку величины
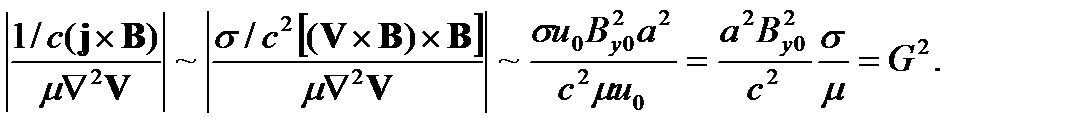
При уменьшении числа Гартмана влияние магнитного поля уменьшается. При этом очевидно, что
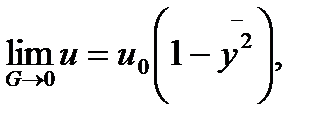
т.е. в предельном случае отсутствия магнитного поля получается классическое плоское течение Пуазейля.
Интересно, что течение Гартмана можно получить, не прибегая к уравнению индукции магнитного поля (1), при выводе которого исключалось электрическое поле и плотность электрического тока при помощи уравнений Максвелла для стационарного случая
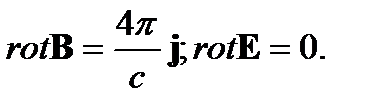(6)
Из второго уравнения следует в нашем случае
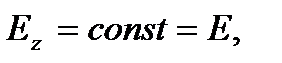(7)
а электромагнитная сила в уравнении движения вычисляется с использованием обобщенного закона Ома
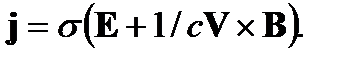
Тогда получим
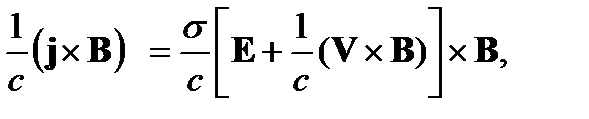
а вместо уравнения (2) в проекции на ось Ох с использованием (7) и этого выражения для электромагнитной силы, будет иметь
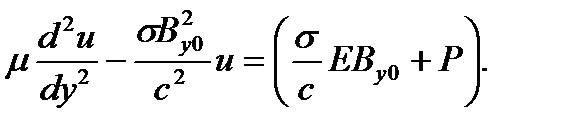
Поскольку правая часть этого линейного уравнения второго порядка относительно скорости течения постоянная, то оно легко решается при граничных условиях (4) на стенках канала. Компонента х магнитного поля вычисляется теперь из первого уравнения (6), а именно, из проекции этого уравнения на ось Оz
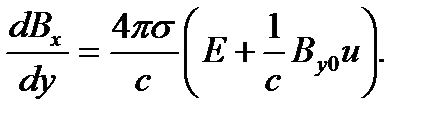
Физический смысл такого решения заключается в том, что течение Гартмана можно создать не только перепадом статического давления, но и при помощи пропускания электрического тока вдоль оси, перпендикулярной плоскости течения (заданное постоянное электрическое поле Е), и приложением перпендикулярно стенкам магнитного поля.
Лекция 11. 29.11.16
В конце Лекции 1 было отмечено, что в классической магнитной гидродинамике, которая рассматривалась во всех остальных наших лекциях, не учитывается вращение заряженных частиц в магнитном поле. Этим вращением можно пренебречь только в том случае, если время их свободного пробега (время между их столкновениями) много меньше периода полного оборота вокруг направления магнитного поля. Ниже мы рассмотрим влияние такого движения на макроскопическое движение электропроводных жидкостей и газов.
Для простоты рассмотрим полностью ионизованный водородный газ, состоящий из электронов и протонов, который обычно называется полностью ионизованной водородной плазмой. Из Лекции 1 очевидно, что в этом случае плотность заряда и плотность электрического тока определяются формулами
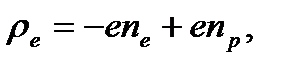
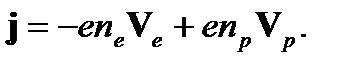(1)
Здесь n e, n p, V eи V pплотности и скорости электронов и протонов, соответственно. Вывести уравнения для макроскопических скоростей электронов и протонов можно на основе кинетических уравнений Больцмана для электронов и протонов, используя метод моментов. Однако мы используем метод двух взаимопроникающих и взаимодействующих континуумов, состоящих из электронов и протонов. Законы сохранения массы импульса и энергии можно получить из интегральных соотношений, как мы это делали в Лекции 2. Уравнения движения для электронов и протонов, при этом, будут иметь вид (для простоты, не будем учитывать вязкость электронов и протонов)
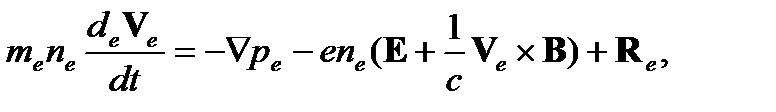
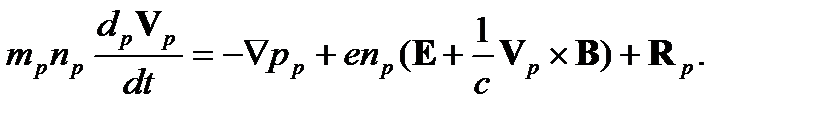
Здесь
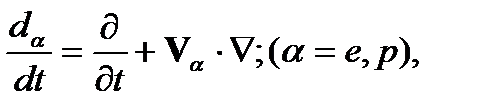
Rα – сила «трения», которая определяет взаимодействие между двумя континуумами. Очевидно, что при этом имеет место соотношение
R е + R р = 0. (2)
Из кинетической теории газов в предположении максвелловской функции распределения по скоростям, а, качественно, из физических соображений выражение для обмена импульсами между компонентами можно записать в виде
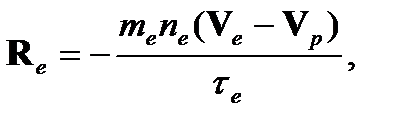(3)
где τе – время свободного пробега электронов.
Из выписанных выше уравнений движения для электронов и протонов с учетом (2) можно получить обобщенный закон Ома, который будет отличаться от аналогичного закона, полученного в Лекции 4 (уравнение (6)). Действительно, умножим уравнение движения для электронов на - e / m e, а уравнение движения для протонов на e / m eи сложим полученные уравнения, пренебрегая членами, в которых в знаменателе стоит mp по сравнению с членами, где в знаменателе стоит масса электрона. В результате будем иметь
(4)
Конечно, здесь предполагается, что имеет место квазинейтральность (ne≈ np), а (ре ~ рр). Поскольку для средней скорости плазмы имеем
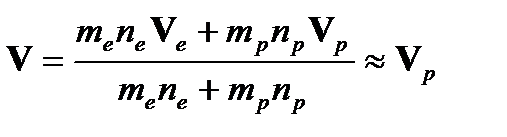
вследствие me << mp, то, вместо уравнения (4), получим, если еще учесть определение (1) для плотности тока,
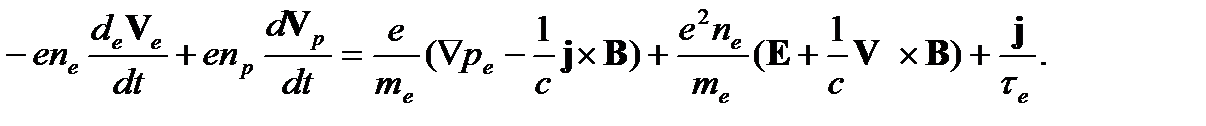
Отношение левой части этого уравнения к последнему члену правой части имеет порядок величины, равный τe / t*, где t *– характерное время задачи. В гидродинамике это время должно быть велико по сравнению с временем свободного пробега частиц, т. е. должно выполняться неравенство τe / t *<< 1. Пренебрегая при этом левой частью последнего уравнения, окончательно получим
(5)
где ϭ – электропроводность. Для полностью ионизованной плазмы она определяется формулой
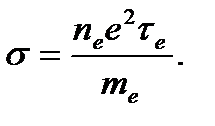
Обобщенный закон Ома (5) отличается от аналогичного закона в магнитной гидродинамике (уравнение (6) в Лекции 4) последним членом правой части. Его отношение к левой части этого уравнения имеет порядок ωeτe, где ωe – циклотронная частота вращения электронов вокруг направления магнитного поля (см. Лекцию 1). При ωeτe ≥ 1 этот член важен и определяет так называемые токи Холла. Для того, чтобы последнее неравенство выполнялось в лабораторных условиях, необходимо в соответствующих установках создавать достаточно сильные магнитные поля. Это неравенство почти всегда удовлетворяется в условиях космической плазмы. Уравнение (5) показывает, что электрический ток в этом случае может течь не только в направлении электрического поля, но и в перпендикулярном к нему направлении. Такие токи и называются токами Холла, а электропроводность становится анизотропной относительно магнитного поля.
Анизотропными относительно направления магнитного поля становятся в этом случае также вязкость и теплопроводность. Приведем пример, связанный с теплопроводностью. Как известно из газовой динамики, потоки тепла пропорциональны градиенту температуры (закон Фурье), а коэффициент теплопроводности зависит от термодинамических параметров. В случае, если газ, состоящий из заряженных частиц, помещен в магнитное поле, то частицы вращаются вокруг направления магнитного поля. Если выполняется условие ωeτe ≥ 1, то, как видно из приложенного рисунка, на котором градиент температуры направлен параллельно оси Ox, а магнитное поле перпендикулярно плоскости рисунка, то частицы, пересекающие выделенную площадку на оси Ox сверху, приходят из области с меньшей температурой, чем частицы, пересекающие ее снизу. В результате столкновений частиц возникают потоки тепла, перпендикулярные как градиенту температуры, так и направлению магнитного поля. При этом очевидно, что магнитное поле, параллельное градиенту температуры, не изменит потоков тепла, которые направлены вдоль этого градиента. Аналогичные соображения приводят и к анизотропии вязкости в магнитном поле.
Лекция 12. 06.12.16
Уравнение индукции магнитного поля при наличии токов Холла.
Обобщенный закон Ома при наличии токов Холла, как было показано на прошлой лекции имеет вид
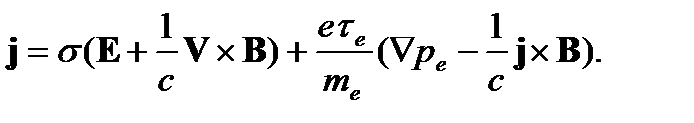
Если использовать теперь уравнения Максвелла в пренебрежении током смещения
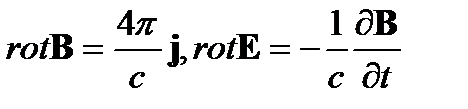
для исключения электрического поля и плотности тока, то получим, вместо уравнения индукции магнитного поля в классической магнитной гидродинамике, следующее уравнение (при ϭ = const)
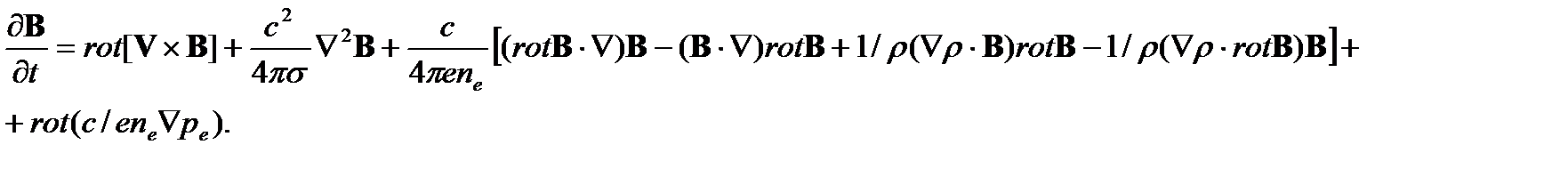Если в этом уравнении перейти к безразмерному виду, то для главных членов в магнитной гидродинамике будем иметь уравнение
(1)
где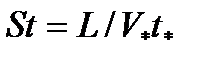 
- число Струхаля (L,V *и t * - характерные длина, скорость и время, соответственно), 
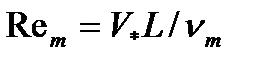- магнитное число Рейнольдса, ωе и τе циклотронная частота вращения электронов и время их свободного пробега, соответственно. Почти весь наш курс лекций был основан на использовании уравнений идеальной магнитной гидродинамики, когда последними двумя членами уравнения (1) можно было пренебречь и справедлив был эффект «вмороженности» магнитного поля. При их наличии этот эффект отсутствует. К каким другим физическим эффектам приводят эти члены?
В обычной гидродинамике вязкие эффекты зависят от величины числа Рейнольдса и определяют, например, затухание распространяющихся в жидкости или газе волн. В магнитной гидродинамике к затуханию волн приводит не только обычная вязкость, но и «магнитная вязкость», определяемая магнитным числом Рейнольдса. Если Rem<< Re, то очевидно, что затухание волн в магнитной гидродинамике происходит в основном за счет «магнитной вязкости», определяемой оператором Лапласа в уравнении (1). Третий член этого уравнения, который учитывает токи Холла, определяет дисперсию волн, т. е. зависимость скорости их распространения от длины волны (или от волнового числа k), а не затухание волн или их диссипацию.
| Рис. 2 |
| Рис. 1 |
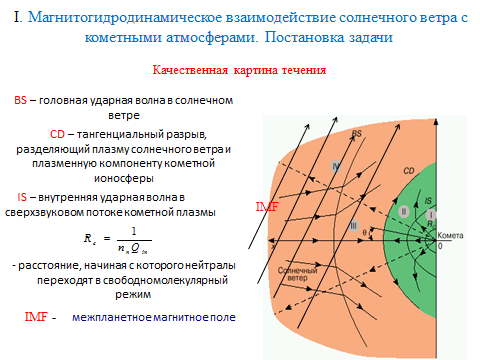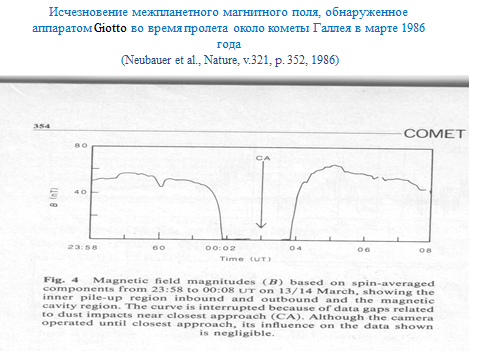
В заключение курса лекций приведу пример, в котором данные эксперимента могут быть объяснены при использовании уравнения (1). Этот эксперимент связан с исследованием кометы Галлея при помощи космических аппаратов в марте 1986 года. На Рис. 1 приведена качественная картина обтекания кометной атмосферы солнечным ветром. Здесь CD– поверхность сильного разрыва (тангенциальный разрыв), разделяющая солнечный ветер с межпланетным магнитным полем (желтый цвет) и плазму кометного газа, в которой нет магнитного поля (зеленый цвет). Единственный космический аппарат, который пересек область, окрашенную в зеленый цвет, был аппарат «Джотто», запущенный Европейским Космическим Агенством (ESA).На Рис. 2 представлено открытие, которое было сделано на этом аппарате при помощи магнитометра, который измерял межпланетное магнитное поле, а именно, исчезновение магнитного поля в течение примерно двух минут, т. е. было доказано, что в коме кометы Галлея нет магнитного поля, а, значит, комета не имеет собственного магнитного поля. Разрывы остальных параметров показали, что CDна Рис. 1 является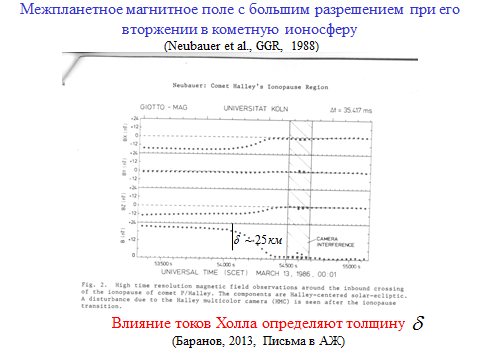 
тангенциальным разрывом. Однако, более детальное измерение магнитного поля, изображенное на Рис. 3, показало, что магнитное поле меняется постепенно от межпланетного до нулевого в
| Рис. 3 |
Попытаемся определить толщину δ в предположении, что она определяется токами Холла. Как известно из гидродинамики, толщина вязкого пограничного слоя определяется равенством инерционных и вязких сил, т. е.
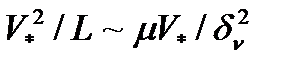
или
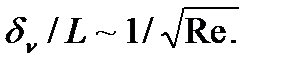
Аналогично оценивается и толщина слоя, определяемого «магнитной вязкостью», т. е. по отношению первого члена справа в (1) ко второму. При этом получим
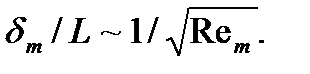(2)
В отличие от оператора Лапласа, в третий член справа в уравнении (1) входят смешанные вторые производные от B. Примерное равенство этого члена с первым дает формулу для толщины проникновения межпланетного магнитного поля δ в кометную плазму вследствие эффекта Холла (см. Рис. 3), а именно,
(3)
Подстановка в это соотношение значений измеренного магнитного поля солнечного ветра вблизи тангенциального разрыва CDи экспериментальных значений параметров кометной плазмы вблизи этого разрыва, измеренных на аппарате «Джотто» дают величину δ ~ 25 км, что соответствует данным магнитометр, изображенным на Рис. 3. Толщина же этого слоя, посчитанная по формуле (2), оказывается существенно меньшей.
Следует также отметить, что толщина магнитопаузы, образуемой вследствие обтекания магнитного поля Земли солнечным ветром, по экспериментальным данным, полученным на спутниках, равна примерно 100 км. Такая же оценка следует и из формулы (3).
ЛИТЕРАТУРА
1. Куликовский А.Г., Любимов Г.А. Магнитная гидродинамика. М. Физматгиз. 1962.
2. Баранов В.Б., Краснобаев К.В. Гидродинамическая теория космической плазмы. М. Изд. «Наука», 1976
3. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М. ГИТТЛ, 1957.
4. Баранов В.Б. О влиянии токов Холла на проникновение магнитного поля через тангенциальные разрывы в незамагниченную плазму в физических условиях космического пространства, Письма в АЖ, т. 39, № 11, 2013.
