Рассмотрим точное решение выписанных выше уравнений для несжимаемой жидкости. Тогда замкнутой системой уравнений будет уравнение (2), уравнение неразрывности в виде
и уравнение индукции магнитного поля в форме (12) прошлой лекции при постоянной плотности, а, именно,
(7)
Рассмотрим нестационарное и одномерное течение, т.е. решение для неизвестных функций будем искать в виде f=f (x,t). Из уравнения неразрывности и уравнения div B= 0 в этом случае получим
Для компонент векторов принимаются обозначения V ={ u, v, w }; B= { B x, B y, B z}. Из последних соотношений следует, что u = u (t) и B x= B x0(t). Если предположить, что компонента скорости u на бесконечности равна нулю, то получим, что всюду u =0. Проекции уравнения (2) на оси Oyи Ozкоординат дают
Эти два уравнения можно свести к одному векторному, вводя векторы V τ{0, v, w } и B τ{0, B y, B z}. В результате получим векторное уравнение
(8)
Проекция уравнения индукции магнитного поля (7) на ось Oxдает
т.е. B x0 = const, а проекции на оси Oyи Ozприводят к двум скалярным уравнениям
которые сводятся к одному векторному
(9)
Исключая из (8) и (9) перекрестным дифференцированием B τили V τ, получаем волновые уравнения
решение которых можно представить в виде
V τ= V τ(x ± V Аt), B τ= B τ(x ± V Аt).
Это решение представляет собой волны, распространяющиеся вдоль оси Oxсо скоростью V А, равной
Эта скорость называется альфвеновской, а сами волны называются волнами Альфвена по имени Нобелевского лауреата, известного шведского ученого – основателя науки, которая называется магнитной гидродинамикой.
Волны Альфвена являются поперечными волнами, поскольку колебания испытывают только компоненты магнитного поля и скорости, перпендикулярные направлению распространения волны. При этом они могут быть произвольной амплитуды. Как мы увидим в дальнейшем, для сжимаемого газа такие волны существуют только для малых амплитуд колебаний.
Лекция 6. 25.10.16
Распространение малых возмущений в МГД.
Рассмотрим волны, которые могут распространяться в сжимаемом, электропроводном газе. Для этого будем использовать уравнения (1), (2), (5) и (6) прошлой лекции, которые запишем в координатной форме. Будем иметь: уравнение неразрывности
уравнение движения в проекциях на оси Ox, Oyи Oz
проекции уравнения индукции магнитного поля (здесь используется это уравнение в форме (12) Лекции 4 при учете уравнения неразрывности)
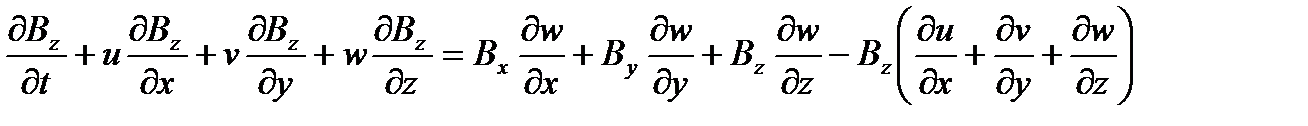
и адиабатический закон, который запишем в виде
.
Решение этой системы уравнений будем искать в виде
(1)
где вторые слагаемые представляют собой возмущения, которые распространяются по газу, течение которого известно (индекс «0») и удовлетворяют выше написанным уравнениям. Ниже будем считать возмущения малыми, т.е. их квадратичные члены пренебрежимо малы, газ покоится (V0= 0), давление и плотность в покоящемся газе постоянны, а систему координат выберем так, чтобы постоянное магнитное поле лежало в плоскости Oxy, т.е.
(2)
Если ввести компоненты возмущенной скорости и магнитного поля по формулам
подставить (1) и (2) в вышенаписанную систему дифференциальных уравнений и пренебречь квадратичными членами, то получим следующую линейную систему уравнений относительно малых возмущений
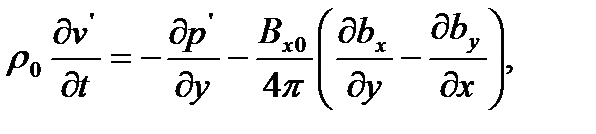
Решение этой линейной системы дифференциальных уравнений будем искать в виде
, (*)
где под 
понимается любая из параметров возмущения, 
- постоянная амплитуда возмущений, 
– частота, 
- волновое число. Подставляя для всех неизвестных функций решение в форме (*), получим однородную систему алгебраических уравнений относительно постоянных амплитуд возмущений.
Из уравнения неразрывности
. 
(3)
Из уравнения движения
, 
. (4)
Из адиабатического закона
(5)
Из уравнения индукции магнитного поля будем иметь
. (6)
Получили систему восьми однородных алгебраических уравнений для определения восьми постоянных амплитуд возмущений. Для существования нетривиального решения
определитель системы уравнений (3) – (6) должен быть равен нулю. Введем скорость распространения возмущения
и заметим, что последние уравнения из (4) и (6) содержат только неизвестные 
и 
. Равенство нулю определителя этой подсистемы из двух уравнений дает один из корней полной системы уравнений (3) – (6), а именно
. (7)
Это есть скорость альфвеновской волны, которая в сжимаемом газе возможна только для волн малой амплитуды. Как мы видели из Лекции 5, в несжимаемой среде такие волны могут быть произвольной амплитуды.
Определитель оставшейся подсистемы легче всего вычислить методом исключения, предположив, при этом, что 
. Выразив 
, 
и 
через 
и 
из (3), второго уравнения (4) и уравнения (5), соответственно, и подставив полученные выражения в первое уравнение (4) и второе уравнение (6), получим уравнения для возмущений плотности и y – компоненты магнитного поля. Равенство нулю определителя этой системы алгебраических уравнеий дает следующее биквадратное уравнение для определения скоростей распространения остальных возмущений.
Корни этого уравнения равны
. (8)
Здесь 
, 
определяется формулой (7). Решение (8) определяет скорости распространения быстрой (знак «+») и медленной (знак «-») магнитозвуковых волн. Очевидно, что при B 0= 0, быстрая магнитозвуковая волна сводится к скорости звука 
в классической газовой динамике.
Лекция 7. 01.11.16
Найдем теперь амплитуды возмущений в различных видах рассмотренных на прошлой лекции волн. Для этого систему уравнений (3) – (6) прошлой лекции разделим на две подсистемы, одна из которых определяет амплитуды альфвеновских волн, а другая - амплитуды быстрых и медленных магнитозвуковых волн. Для альфвеновских волн будем иметь следующие уравнения для амплитуд возмущений
(1)
Подсистема для остальных волн будет иметь вид
(2)
Прежде чем рассмотреть вопрос о том, какие амплитуды возмущенных параметров отличны от нуля в различных рассмотренных волнах, исследуем сначала волны, которым соответствует корень алгебраической системы однородных уравнений (1) и (2), равный нулю (а = 0).
Подставляя этот корень в систему уравнений (1) и (2), получим, что все амплитуды возмущенных функций равны нулю, кроме плотности, т.е. 
Изменение плотности при неизменных остальных параметрах означает изменение энтропии. Поэтому такие волны называются энтропийными, которые не распространяются в газе, т. е.
Альфвеновские волны.
Как мы видели из прошлой лекции, скорость альфвеновской волны определяется из равенства нулю определителя системы уравнений (1) и равна
. (3)
Подстановка величины (3) в систему уравнений (2) дает тривиальное решение для этой подсистемы (эта величина не является корнем определителя этой системы). В результате получим
(4)
Подстановка же (3) в (1) дает
т.е. в альфвеновских волнах флуктуации испытывают только компоненты, нормальные направлению их распространения. Такие волны называются поперечными.
Здесь следует заметить, что альфвеновские волны в несжимаемой жидкости, которые мы рассматривали в Лекции 5, могут быть произвольной амплитуды. Волны же Альфвена в сжимаемом газе, как мы видели выше, могут быть только малой амплитуды.
Быстрые и медленные магнитозвуковые волны.
Скорости быстрых и медленных магнитозвуковых волн определяются из равенства нулю определителя системы уравнений (2). Эти скорости равны (см. Лекцию 6) 
(5)
Если подставить (5) в систему уравнений (1), то получим, что
т.е. поперечные колебания в этих волнах отсутствуют. Подстановка же (5) в (2) приводит к отличию от нуля всех амплитуд, которые равны нулю в альфвеновских волнах (см. (4)). Из (5) следует, что при В 0 = 0 скорость медленной магнитозвуковой волны стремится к нулю, а скорость быстрой волны стремится к скорости звука в обычной газовой динамике. Из (5) очевидно, что скорости распространения быстрых и медленных магнитозвуковых волн зависят от направления магнитного поля, поскольку
Рассмотрим сначала два частных случая:
.
Из (5) в этом случае видно, что в перпендикулярном к магнитному полю направлении медленная магнитозвуковая волна не распространяется, а скорость быстрой магнитозвуковой волны равна
.
Из (5) видно, что при магнитном поле, направленном вдоль распространения волны, возможны два подслучая.
При 
имеем
(6)
Из (6) видно, что вдоль магнитного поля быстрая магнитозвуковая волна распространяется с обычной скоростью звука в газовой динамике, а скорости медленной магнитозвуковой и альфвеновской совпадают. Можно нарисовать диаграмму распространения малых возмущений в этом подслучае, как функцию угла наклона постоянного магнитного поля к оси абсцисс (угол α).
При
из (6) получаем в этом подслучае
(7)
т.е. скорость быстрой магнитозвуковой волны совпадает с альфвеновской, а медленной – со скоростью звука без магнитного поля. Диаграмма распространения малых возмущений в этом случае будет иметь вид, представленный на следующем рисунке.
Легко доказать, что диаграмма для распространения альфвеновской волны является окружностью. При этом всегда имеют место неравенства
Слабые разрывы в магнитной гидродинамике.
Поверхностью слабого разрыва некоторых функций будем называть такую поверхность, на которой терпят разрыв производные при непрерывности самих функций. Если сами функции терпят разрыв на некоторой поверхности, то такие поверхности называются поверхностями сильного разрыва и будут нами рассмотрены в следующей лекции.
Поверхности, на которых возможен слабый разрыв решения некоторой системы дифференциальных уравнений, являются характеристическими поверхностями для этой системы дифференциальных уравнений. Пусть плоскость yOz совпадает с поверхностью слабого разрыва, а ось Оx перпендикулярна ей. Если через фигурные скобки обозначить разность производных слева и справа от этой поверхности в какой-либо ее точке, то имеем для производных искомых функций
Действительно, если бы эти производные были отличны от нуля, то в соседних точках этой поверхности сами функции терпели бы разрыв. Запишем теперь замкнутую систему уравнений магнитной гидродинамики в координатной форме (см. начало Лекции 6) слева и справа от поверхности слабого разрыва и вычтем одну систему из другой. Будем иметь
Из уравнения div B= 0также следует
а, значит, что и
Поскольку функции на поверхности слабого разрыва непрерывны, то для любой из функций можно записать
или
где dx/dt – скорость поверхности слабого разрыва. Вводя скорость слабого разрыва относительно газа
и подставляя это соотношение в выписанные выше уравнения для слабого разрыва, получим систему однородных уравнений для разрывов производных функций по координате x
Приравнивая определитель этой системы уравнений к нулю, получим уравнение для определения скоростей распространения слабых разрывов
Здесь введено обозначение для скорости звука 
в отсутствие магнитного поля.
Это уравнение имеет те же корни, что и уравнение для определения скоростей распространения малых возмущений (см. (3) и (6)), т.е.
Отличие заключается в том, что, скорости распространения слабых разрывов зависят от параметров газа, которые заранее неизвестны (малые возмущения распространялись по покоящемуся газу с постоянными давлением, плотностью и магнитным полем).
Лекция 8. 08.11.16
