Лабораторная работа № 2-3
СИСТЕМЫ СЧИСЛЕНИЯ
Цель работы: Изучение арифметических основ ЭВМ.
Вопросы:
1. Понятие систем счисления.
2. Позиционные и непозиционные системы счисления.
3. Перевод чисел из одной системы счисления в другую.
4. Арифметические действия над числами в различных системах счисления
amp; Теоретические сведения
1. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример 1. Число 2210 перевести в двоичную систему счисления.

2210 = 101102
2. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример 2. Число 57110 перевести в восьмеричную систему счисления.
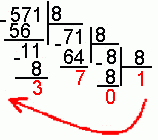
57110 = 10738
3. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример 3. Число 746710 перевести в шестнадцатеричную систему счисления.

746710 = 1D2B16
4. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:
Таблица 1. Степени числа 2
| n степень | |||||||||||

|
Пример 4. Число 111010002 перевести в десятичную систему счисления.
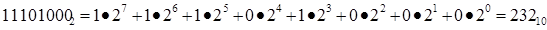
5. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 2. Степени числа 8
| n (степень) | |||||||

|
Пример 5. Число 750138 перевести в десятичную систему счисления.

6. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 3. Степени числа 16
| nстепень | |||||||

|
Пример 6. Число FDA116 перевести в десятичную систему счисления.

7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 4).
Таблица 4. Таблица соответствия восьмеричных цифр и двоичного кода
| Двоичный код | Восьмеричная цифра | Десятичный эквивалент | |
Пример 7. Число 10010112 перевести в восьмеричную систему счисления. 001 001 0112 = 1138
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей шестнадцатеричной цифрой (табл. 5).
Таблица 5. Таблица соответствия шестнадцатеричных цифр и двоичного кода
| Двоичный код | Шестнадцатеричная | Десятичный эквивалент |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
Пример 8. Число 10111000112 перевести в шестнадцатеричную систему счисления.
0010 1110 00112 = 2E316
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример 9. Число 5318 перевести в двоичную систему счисления.
5318 = 1010110012
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример 10. Число EE816 перевести в двоичную систему счисления.
EE816 = 1110111010002
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 11. Число FEA16 перевести в восьмеричную систему счисления.
FEA16 = 1111111010102
111 111 101 0102 = 77528
Пример 12. Число 66358 перевести в шестнадцатеричную систему счисления.
66358 = 1101100111012
1101 1001 11012 = D9D16
12. Если переводится дробная часть числа, то она умножается на Р (основание системы счисления, в которую переводится число), после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на Р и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием Р.
Пример 13. Число 0, 12510 перевести в двоичную систему счисления
0,12510® Х2 = 0,0012
| ,125 | * 2 | |
| ,25 | * 2 | |
| ,5 | * 2 | |
| ,0 | * 2 |
13. Для сложения многоразрядных чисел используется метод, аналогичный тому, с помощью которого складывают десятичные числа на бумаге. Числа складываются поразрядно, начиная с младшего разряда, причём, если сумма цифр некоторого разряда превышает основание системы счисления, то к следующему разряду прибавляется единица, а в данный разряд записывается разность между получившейся суммой и основанием системы счисления.
0 1 0 1
+0+0+1+1
 0 1 1 1 1
0 1 1 1 1
перенос
Примеры.
1). 458 + 368 = 1038
1
36 4+3+1=810=1∙8+0=108
| 5). 3816 + 2516 = 5D16
5D
| ||||
1. 2). 2748 + 768 = 3728
1 1
372 2+1=3
| 6). 78C16 + 9B16 = 82716
1 1
9B 1+8+9=1810=1∙16+2=1216
| ||||
3). 5218 + 3778 = 11208
1 1
377 1+2+7=1010=1∙8+2 = 128 1120 | 7). B8C416 + F9D16 = C86116
1 1 1
C861 1+8+F=1+8+15=2410=1∙16+8=1816 1+B=1+11=1210=C16
| ||||
4). 1А,2416 + 31,B516 = 4B,D916
4B,D9 A+1=10+1=1110=B16 1+3=4
| 8). F4716 + D9816 = 1CDF16
1CDF F+D=15+13=2810=1∙16+12=1C16
|
14. Вычитание, так же как и сложение, выполняется поразрядно, начиная с младшего разряда. Если в некотором разряде уменьшаемое меньше вычитаемого, то «занимается» единица из старшего разряда, т.е. старший разряд уменьшается на единицу, а данный разряд увеличивается на число, равное основанию системы счисления.
Примеры.
1). 2358 – 718 = 1448
∙ 8
| 5). A516 – 1916 = 8C16
∙ 16
8 C | ||||
2). 2138 – 468 = 1458
∙ ∙ 8
46
| 6). 57C16 – 8F16 = 4ED16
∙ ∙ 16
4ED
| ||||
3). 14358 – 7468 = 4678
∙ ∙ ∙ 8
746 8+2-4=6 467 | 7). 9A2316 – ABC16 = 8F6716
∙ ∙ ∙ 16
A B C 16+1-B=16+1-11=6
| ||||
4). 3218 – 238 = 2768
∙ ∙ 8
23 8+1-2=7
| 8). D54316 – 69B16 = CEA816
∙ ∙ ∙ 16
6 9 B 16+3-9=1010=A16
|
15. Умножение многозначных чисел выполняется аналогично «в столбик». Умножение этим способом сводится к перемножению однозначных чисел и сложению.
Примеры.
1). 538 · 48 = 2548
1
| 5). 1516 · 616 = 7E16
1
7E
| ||||||||
2). 175 8· 0,58 = 116,18
4 3
0,5 7·5+3=3810=4∙8+6=468
| 6). 14916 · 8916 = B01116
89 4·9+5=4110=2·16+9=2916
 B91 1·9+2=1110=B16 B91 1·9+2=1110=B16
A48 9·8=7210=4·16+8=4816
1·8+2=1010=A16 9+8=1710=1·16+1=1116 1+B+4=1+11+4=1610=1·16+0=1016
| ||||||||
3). 248 · 168 = 4308
24 7+4=1110=1∙8+3=138 430
| 7). 24E16 · 1216 = 297C
24E 9+E=9+14=2310=1·16+7=1716
| ||||||||
4). 6238 · 418 = 317638
41 2·4+1=910=1∙8+1=118
 623 6·4+1=2510=3∙8+1=318 623 6·4+1=2510=3∙8+1=318
| 8). A,516 · 2,B16 = 1B,B716
2,B A·B+3=10·11+3=11310=7·16+1=7116
 7 1 7 5·2=1010=A16 7 1 7 5·2=1010=A16
1 4 A A·2=10·2=2010=1·16+4=1416
7+4=1110=B16
|
16. Деление многозначных чисел в любой позиционной системе выполняется тем же способом, что и в десятичной. При этом используются операции умножения и вычитания.
Примеры.
Деление на однозначные числа
1) 528: 38 = 168
| 38 | |||
| 168 | ||||
| 1·3=3 6·3=1810=2∙8+2=228 | |||
2) 3138: 78 = 358
| 78 | |||
| 358 | ||||
| 7·3=2110=2∙8+5=258 5·7=3510=4∙8+3=358 | |||
3) 33416: A16 = 5216
| A16 | |||
| 5216 | ||||
| 5·A=5010=3·16+2=3216 2·A=2010=1·16+4=1416 | |||
Деление на многозначные числа
4) 2508: 168 = 148
| 168 | |||||
| 148 | ||||||
| 48·168=708
3
70 1·4+3=7 | |||||
5) 15528: 238 = 568
| 238 | |||||
| 568 | ||||||
| 58·238=1378
1
| |||||
68·238=1628
2
|
 6 2·6+2=1410=1·8+6=168
6 2·6+2=1410=1·8+6=168
6) 5E816: 1216 = 5416
| 1216 | |||||
| 5A | 5416 | |||||
| 516·1216=5A16
5A | |||||
416·1216=4816
|
 4
4
Практическая работа
1. Выполнить перевод чисел: 10, 25, 45, 100 из 10-ой системы в 2-чную,
4-ричную, 8-ричную и в 16-ричную системы счисления.
Результаты проверить обратным переводом.
2. Вычислить значения выражений:
a) 199310- 101100012* 5638 + D316=?
b) 1010012 * 6738 + F316=?
c) 111012 + 10158+ 1АВ16=?
d) 11012* 2738- АВ16=?
e) 1010- 110002+ С1В16=?
3. Сравнить числа (расположить в порядке возрастания или убывания):
a) 2368, 101110112, 3D516, 10210
b) 19210, 111011012, 3258, 11С16
c) 2910, 10011110102, 2548, В116
d) 11210, 4638, 3А16, 101101102
4. Выполните сложение и вычитание чисел в 2-ой системе
a) 11001001 + 10010100
b) 10000101 + 11100010
c) 11100100 + 11101100
d) 11101010 – 10101010
e) 11010100 - 10101000
f) 10101010 - 10001111
5. Выполните сложение и вычитание чисел в 3-ой системе
a) 122 + 100100
b) 101201 + 10012
c) 200 + 1222
d) 2222 - 1222
e) 202020 - 1000
f) 1111 – 222
6. Выполните сложение и вычитание чисел в 8-ой системе
a) 123 + 256
b) 1256 + 4567
c) 2345 + 6770
d) 2341 + 123
e) 777 – 666
f) 6245 - 765
7. Выполните сложение и вычитание чисел в 16-ой системе
a) 1FFF + 2FA
b) 1234 + 3A
c) 435 + 3DA
d) 3AD + 9AF
e) FFF – AAA
f) 2345F – 123
8. В саду 100 фруктовых деревьев - 14 яблонь и 42 груши. В какой системе счисления посчитаны деревья?
: Самостоятельная работа:
1. перевести заданные числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
2. перевести заданные числа в десятичную систему счисления.
3. перевести заданные числа из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления.
4. перевести заданные числа в двоичную систему счисления.
5. Выполнить сложение.
6. Выполнить вычитание.
7. Выполнить умножение.
В отчете по лабораторной работе должен быть представлен подробный протокол перевода всех заданных чисел. В заданиях 5-7 проверить правильность вычислений переводом исходных данных и результатов в десятичную систему счисления.
Варианты
Вариант 1
1. а) 25 б) 45,865 в) 38,762 г) 67,85
2. а) 101101102 б) 3478 в) 56АЕ16 г) 101110111012
3. а) 101110111012 б) 101101101011012 в) 111011100101012
4. а) 57318 б) А56В16 в) 47318 г) 2A9E16
5. а) 101110111012 + 1101011012 б) 3478 + 4518 в) 5АЕ16 + 49С16
6. а) 101110111012 - 1101011012 б) 3478 - 1518 в) 5АЕ16 - 49С16
7. а) 11102 * 1102 б) 2318 * 348 б) 15А16 * Е416
Вариант 2
1. а) 20 б) 35,865 в) 31,765 г) 37,15
2. а) 111011002 б) 4658 в) 91АС16 г) 111001111012
3. а) 111011011102 б) 110110101101012 в) 110111010101012
4. а) 42378 б) С91В16 в) 15728 г) 6С4E16
5. а) 110101111012 + 1010101112 б) 4738 + 6458 в) 5FA16 + 42D16
6. а) 100111111012 - 1010111012 б) 6478 - 1248 в) 6АF16 - 31C16
7. а) 11102 * 1102 б) 2318 * 348 б) 15А16 * Е416
Вариант 3
1. а) 27 б) 33,825 в) 33,73 г) 47,24
2. а) 101111002 б) 4758 в) 68BС16 г) 100111111012
3. а) 111110110102 б) 111011001101012 в) 111010110101012
4. а) 44778 б) С24В16 в) 13478 г) 3B5E16
5. а) 110111110012 + 1011010112 б) 8738 + 2558 в) 3EЕ16 + 23С16
6. а) 111011101012 - 1010111012 б) 5778 - 2748 в) 7АC16 - 25С16
7. а) 11012 * 1012 б) 12F8 * 648 б) 85А16 * F416
Вариант 4
1. а)41 б) 52,865 в) 54,74 г) 37,15
2. а) 101011102 б) 4528 в) 54FС16 г) 111001101002
3. а) 101001011102 б) 010010100100012 в) 010001000101012
4. а) 54378 б) F61В16 в) 15728 г) 62FE16
5. а) 010001101002 + 1010101112 б) 4238 + 5258 в) 7АD16 + 64С16
6. а) 101010001002 - 0100001002 б) 5478 - 1878 в) 3BC16 - 52С16
7. а) 11012 * 1012 б) 4638 * 838 б) 57А16 * 3Е16
Вариант 5
1. а) 64 б)37,864 в) 62,75 г) 42,63
2. а) 100111002 б) 4728 в) 61AF16 г) 100111110012
3. а) 111100110102 б) 110011001001012 в) 110010100101012
4. а) 16378 б) 83СF16 в) 16778 г) 75FA16
5. а) 100111110012 + 1010010112 б) 4238 + 2438 в) 5AЕ16 + 73С16
6. а) 110011001012 - 1010110012 б) 3658 - 3148 в) 4АF16 - 54С16
7. а) 10012 * 1112 б) A 516 * D 416 б) 85А16 * Е416
Вариант 6
1. а) 20 б) 63,865 в)74,75 г)75,37
2. а) 110011002 б) 1648 в) 53FC16 г) 110001110012
3. а) 110011011002 б) 110101101101012 в) 110110010101012
4. а) 27478 б) 53СF16 в) 57128 г) 63СE16
5. а) 110101110012 + 1011010112 б) 7348 + 5418 в) 5А616 + 52F16
6. а) 101100110012 - 1011010112 б) 7348 - 1158 в) 6АF16 - 42С16
7. а) 11002 * 1112 б) 3F16 * 3A16 б) 64A16 * 4Е16
Вариант 7
1. а) 53 б) 36, 582 в) 42,73 г) 463,24
2. а) 110011002 б) 6238 в) 86BF16 г) 101001111012
3. а) 111111000102 б) 111100010001012 в) 111011000101012
4. а) 47478 б) 42AВ16 в) 34178 г) 37AE16
5. а) 111001110012 + 1100011002 б) 8428 + 6358 в) 26Е16 + 64С16
6. а) 111100101012 - 1011001012 б) 7278 - 2648 в) 36C16 - 62С16
7. а) 10112 * 1012 б) 75F16* D416 б) 53А16 * 6Е16
Вариант 8
1. а)64 б) 42,853 в) 21,23 г) 23,65
2. а) 101101012 б) 5258 в) 43АA16 г) 111110011012
3. а) 110111011102 б) 110101110101012 в) 110111010101012
4. а) 74238 б) A41A16 в) 25318 г) 6A0A16
5. а) 011111101012 + 1101101012 б) 6458 + 4328 в) 6EЕ16 + 87С16
6. а) 111011011012 - 1101101012 б) 5438 - 1868 в) 9EA16 - 52A16
7. а) 10112 * 1012 б) 5216 * 3A16 б) 15F16 * E816
Вариант 9
1. а) 72 б) 42,825 в) 76,73 г) 45,31
2. а) 111110002 б) 5418 в) 42AС16 г) 111001111012
3. а) 111011011102 б) 111110110001012 в) 111011010110012
4. а) 47748 б) D24В16 в) 13538 г) 2E7E16
5. а) 110111100112 + 1011010112 б) 5238 + 4248 в) 2FЕ16 + 64A16
6. а) 101110111012 - 1001011112 б) 7658 - 6358 в) 4EC16 - 43D16
7. а) 10012 * 1002 б) 73D16 * D616 б) 86А16 * Е916
Вариант 10
1. а) 46 б) 14,863 в) 85,07 г) 42,64
2. а) 101101102 б) 2758 в) 53EС16 г) 111100111012
3. а) 100011011102 б) 101011010001012 в) 101010101111012
4. а) 83678 б) A63В16 в) 72428 г) 7С4D16
5. а) 110101100012 + 1110101012 б) 7438 + 1458 в) 4АF16 + 62С16
6. а) 101011111012 - 1100011012 б) 4378 - 5118 в) 4BC16 - 83616
7. а) 10002 * 1112 б) 61D16 * E416 в) 37E16 * A316
Вариант 11
1. а) 72 б) 77,465 в) 85,65 г) 36,57
2. а) 101001112 б) 7358 в) 86AС16 г) 100100111012
3. а) 100100110102 б) 111110001101012 в) 111110100101012
4. а) 45278 б) A84F16 в) 15438 г) 5B5A16
5. а) 110000110012 + 1011100112 б) 4518 + 5688 в) 3AЕ16 + 85С16
6. а) 1110111001012 - 1001011112 б) 5368 - 7448 в) 8FD16 - 21С16
7. а) 10012 * 0112 б) 85A16 * C616 б) 73А16 * F916
Вариант 12
1. а) 63 б) 15,745 в) 52,76 г) 52,75
2. а) 011111002 б) 3458 в) 61АF16 г) 100001001012
3. а) 111111011002 б) 101101011101012 в) 101010110001012
4. а) 38678 б) F91A16 в) 17528 г) 3F4A16
5. а) 110111101012 + 1101001112 б) 8458 + 4778 в) 6АD16 + 17С16
6. а) 101111101102 - 1110010112 б) 8378 - 1158 в) 5FF16 - 50A16
7. а) 11102 * 1102 б) 73D16 * D616 б) 86А16 * Е916
Вариант 13
1. а) 27 б) 33,825 в) 33,73 г) 47,24
2. а) 101111002 б) 4758 в) 68BС16 г) 100111111012
3. а) 111110110102 б) 111011001101012 в) 111010110101012
4. а) 44778 б) С24В16 в) 13478 г) 3B5E16
5. а) 110111110012 + 1011010112 б) 8738 + 2558 в) 3EЕ16 + 23С16
6. а) 111011101012 - 1010111012 б) 5778 - 2748 в) 7АC16 - 25С16
7. а) 11012 * 1012 б) 73D16 * D616 б) 86А16 * Е916
Вариант 14
1. а) 95 б) 22,833 в) 48,73 г) 95,37
2. а) 110010112 б) 6258 в) 84ED16 г) 111111100012
3. а) 111101101102 б) 110110110101012 в) 110101111010012
4. а) 72578 б) A73F16 в) 73328 г) 6E9F16
5. а) 111111010012 + 1011010112 б) 7338 + 6658 в) 2АF16 + 85A16
6. а) 110111101012 - 1100101112 б) 6648 - 7718 в) 2DC16 - 76E16
7. а) 10002 * 1002 б) 51D16 * A216 б) 22E16 * C616
Вариант 15
1. а) 74 б) 34,823 в) 38,46 г) 53,85
2. а) 101111002 б) 6358 в) 38Bф16 г) 100111111012
3. а) 111101110102 б) 111010110011012 в) 111010101101012
4. а) 46678 б) С29В16 в) 17378 г) 5B9E16
5. а) 111111010012 + 1011010112 б) 8638 + 5558 в) 3BB16 + 23С16
6. а) 101110111012 - 1010101112 б) 4278 - 2738 в) 7АD16 - 26С16
7. а) 11112 * 0012 б) 36D16 * A416 б) 35А16 * Е616
Вариант 16
1. а) 65 б) 63,875 в) 53,75 г) 37,87
2. а) 011101102 б) 4428 в) 32AA16 г) 111110011012
3. а) 101110111102 б) 110000001101012 в) 111110100101012
4. а) 45378 б) A45В16 в) 15558 г) 5A3E16
5. а) 110110111102 + 1011010112 б) 5438 + 6558 в) 5АA16 + 49F16
6. а) 111011101012 - 1010111012 б) 3238 - 1638 в) 5CC16 - 52С16
7. а) 10112 * 1112 б) 54D16 * A616 б) 43А16 * Е916
Вариант 17
1. а) 32 б) 46,843 в) 12,53 г) 23,65
2. а) 100011112 б) 4358 в) 32BA16 г) 101100111112
3. а) 111101110102 б) 111110110001012 в) 111010101011012
4. а) 55578 б) A33В16 в) 17148 г) 3C3E16
5. а) 110111011012 + 1010110112 б) 3638 + 2758 в) 5CЕ16 + 66E16
6. а) 110110111012 - 1001110112 б) 1178 - 5348 в) 6CC16 - 25E16
7. а) 11102 * 1102 б) 15D16 * A616 б) 63А16 * E916
Вариант 18
1. а) 94 б) 37,435 в) 82,76 г) 54,43
2. а) 110110102 б) 5468 в) 33АD16 г) 111111100012
3. а) 111011111002 б) 111011011001012 в) 110101010011112
4. а) 51678 б) С37E16 в) 11628 г) 6A3E16
5. а) 101011111012 + 1011110102 б) 4668 + 2258 в) 7АA16 + 66A16
6. а) 110111011012 - 1101010112 б) 3658 - 1548 в) 5EC16 - 72С16
7. а) 10102 * 1012 б) 36D16 * C616 б) 33А16 * A516
Вариант 19
1. а) 84 б) 76,865 в) 43,73 г) 43,85
2. а) 111110002 б) 3858 в) 65DС16 г) 101110111012
3. а) 111111100102 б) 111110001101012 в) 111110100101012
4. а) 47678 б) С54В16 в) 73578 г) 5B6A16
5. а) 011111011012 + 1011110102 б) 1638 + 4358 в) 3DC16 + 25A6
6. а) 101110111012 - 1011110012 б) 5728 - 5448 в) 5DC16 - 56E16
7. а) 10012 * 1002 б) 74D16 * A316 б) 56D16 * D516
Вариант 20
1. а) 94 б) 27,843 в) 62,23 г) 53,32
2. а) 110000112 б) 5258 в) 85FD16 г) 110001100012
3. а) 11111101102 б) 110101110110012 в) 110101011110012
4. а) 61378 б) E27F16 в) 27128 г) 5C2F16
5. а) 111100111012 + 1011110102 б) 6438 + 8258 в) 3CF16 + 72D16
6. а) 110011111012 - 1101001112 б) 7248 - 7328 в) 2AD16 - 72E16
А) 10112 * 1012 б) 73D16 * A216 б) 52E16 * A416 Вариант 21
1. а) 41 б) 53,433 в) 76,56 г) 5776
2. а) 100111102 б) 8758 в) 87D16 г) 101100111112
3. а) 111101011102 б) 101011011011012 в) 111011010101012
4. а) 56278 б) С76A16 в) 17548 г) 6A4E16
5. а) 101111110012 + 1101010112 б) 3638 + 5458 в) 3AE16 + 57С16
6. а) 101011101112 - 1010110112 б) 4748 - 3278 в) 7DA16 - 74С16
8. а) 10002 * 0112 б) 85A16 * D616 б) 64E16 * A216
Вариант 22
1. а) 37 б) 84,854 в) 62,85 г) 48,62
2. а) 100111012 б) 5438 в) 84AD16 г) 101111011012
3. а) 110111011102 б) 111011110001012 в) 111010101011012
4. а) 57558 б) D73В16 в) 11748 г) 6A7A16
5. а) 111001110112 + 1010101112 б) 7338 + 8458 в) 7CA16 + 73E16
6. а) 111001101112 - 1010011112 б) 3828 - 4878 в) 6AD16 - 47C16
7. а) 11112 * 1002 б) 57E16 * A416 б) 83А16 * D316
? Контрольные вопросы:
1. Дайте определение системе счисления. Назовите и охарактеризуйте свойства системы счисления.
2. Какие системы счисления называют позиционными, а какие непозиционными?
3. Что называется основанием системы счисления?
4. Почему для вычислительной техники особенно важна система счисления по основанию 2?
5. почему произошел переход от двоичной к шестнадцатеричным обозначениям в архитектуре ЭВМ?
6. Какие способы перевода десятичных чисел в другие системы счисления и обратно вы знаете?
7. Каковы правила выполнения арифметических операций над числами в двоичном представлении?
8. Как переводить целые числа из двоичного представления в восьмеричное и шестнадцатеричное представления и обратно?
9. Чему равны веса разрядов слева и справа от точки, разделяющей целую и дробную часть числа, в двоичной, восьмеричной и шестнадцатеричной системах счисления?





 103
103 25 3+2=5
25 3+2=5 76 1+7+7=1510=1∙8+7 = 178
76 1+7+7=1510=1∙8+7 = 178 827
827 1+5+3=910=1∙8+1 = 118
1+5+3=910=1∙8+1 = 118 F9D 1+C+9=1+12+9=2210=1∙16+6=1616
F9D 1+C+9=1+12+9=2210=1∙16+6=1616 31,B5 2+B=2+11=1310=D16
31,B5 2+B=2+11=1310=D16 D98 4+9=13=D
D98 4+9=13=D 71 8+3-7=4
71 8+3-7=4 1 9
1 9 8F 16+6-8=1410=E16
8F 16+6-8=1410=E16 8+3-7=4
8+3-7=4 8 F 6 7 16+9-A=1510=F16
8 F 6 7 16+9-A=1510=F16 276
276 C E A 8 16+4-6=1410=E16
C E A 8 16+4-6=1410=E16 4 5·4+1=2110=2∙8+5=258
4 5·4+1=2110=2∙8+5=258 6 1·6+1=7
6 1·6+1=7 116,1 1·5+4=910=1∙8+1=118
116,1 1·5+4=910=1∙8+1=118 B011 4·8+4=3610=2·16+4=2416
B011 4·8+4=3610=2·16+4=2416 12 4·2+1=9
12 4·2+1=9 297C 1+4+4=9
297C 1+4+4=9 1 B,B 7 1+A=B
1 B,B 7 1+A=B 4 6·4=2410=3·8+0=308
4 6·4=2410=3·8+0=308
