Приклад 7.1. За допомогою спектрофотометричного методу визначення вміст сульфату хініну в таблетках. Виконано 6 вимірювань, які дали такі результати: 99,9; 99,8; 99,6; 99,1; 99,2; 99,2%.
Знайти оцінку вмісту сульфату хініну в таблетках та його дисперсію і стандартне відхилення.
Розв’язання. Оцінкою істинного значення вимірюваної величини Х є її вибіркове середнє, яке розраховується за формулою
Де n – об’єм виборки, xi – i-й елемент виборки.
Вибіркове середнє дорівнює
Дисперсія S2 ознаки Х розраховується за формулою
Підставляючи чисельні значення, знаходимо
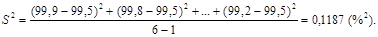
Стандартне (середньоквадратичне) відхилення S ознаки в окремому вимірювання розраховується за формулою
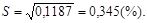
Стандартне відхилення усередненої ознаки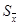 
(стандартне відхилення середнього арифметичного) розраховується за формулою
Воно дорівнює
Зауваження 1. Слід добре розрізняти стандартне відхилення S, яке є характеристикою окремого вимірювання у даній виборці, і стандартне відхилення 
середнього арифметичного, яке є характеристикою сукупності вимірювань.
Зауваження 1. Точність обчислення значення є невисокою, тому недоцільно записувати його більш ніж з двома значущими цифрами. Крім того, точність оцінки значення визначає і точність оцінки середнього значення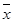 
Приклад 7.2. Вимірювання об’єкту Х ампул 1%-го розчину аскорбінової кислоти в 40%-му розчині глюкози дало середнє значення 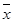=10 мл з дисперсією 
мл2. Знайти:
а) Вірогідний інтервал для середнього об’єму всієї партії ампул з надійністю P=0,95, якщо вибірка становила 50 ампул.
б) Вірогідність того, що відхилення (півширина вірогідного інтервалу) не перевищує 
мл, якщо виборка становила 50 ампул.
в) Об’єм виборки, при якому гарантується гранична похибка мл з надійністю P=0,95.
Розв’язання. Оскільки дисперсія відома, використаємо статистику
,
Яка підпорядковується стандартному нормальному розподілу N(0;1).
а) Завдання вимагає знайти такий проміжок 
, що математичне сподівання об’єму ампули (його дійсне значення) з ймовірністю 0,95 знаходиться у цьому проміжку. Приналежність мат. Сподівання величини Х до проміжку відповідає приналежності величини Z до деякого проміжку 
з тією самою ймовірністю 0,95. Оскільки величина Z має розподіл N(0;1), то ця ймовірність дорівнює
де Ф(z) – функція розподілу нормованої нормально розподіленої випадкової величини (розподілу N(0;1)). Враховуючи, що за умовою
Отримуємо рівняння
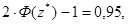
звідки
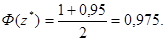
За таблицею значень функції Ф(z)([2] – табл.3 стор.304, [3] – прил.2 стр.297) знаходимо таке z*, що Ф(z)=0,975.
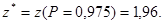
Оскільки на межах вірогідного проміжку маємо співвідношення
то
,
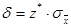або ж
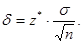
Підставляючи чисельні значення в останню формулу, знаходимо:
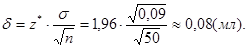
Отже, шуканий вірогідний проміжок для надійності 95% є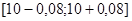 
або 
.
То півширина вірогідного інтервалу 
дорівнює.
Зауваження. Для знаходження значення межевого значення нормова змінної z можна скористатись також таблицями: [1] – табл.2 стор.192, [2] табл.2 стор.303, [3] – прил.3 стр.299. При цьому, оскільки вказані табл. Містять значення інтегралу ймовірності Ф0(z) в межах [0;z], а не [- 
; як таблиці вказані раніше, слід шукати значення z*, таке що
.
У нашому випадку
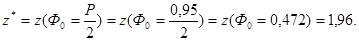
б) З формули для півширини вірогідного проміжку (п.а))
Виражаємо нормовану змінну z*:
.
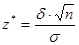Підставивши чисельні значення, обчислимо значення нормальної змінної z що відповідає межам вірогідного проміжку:
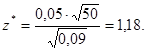
Ймовірність приналежності випадкової величини Х проміжок дорівнює ймовірності приналежності нормованої величини проміжку яка може бути знайдена за допомогою вказаних у п.а таблиць функції розподілу Ф(z) випадкової величини, що має стандартний нормальний розподіл:
За таблицями функції Ф(z) знаходимо
Ф(z*)=Ф(1,18)=0,881
шукана ймовірність дорівнює
б) Виходячи з заданої надійної (довірчої) ймовірності P=0,95, визначаємо визначення нормальної змінної змінної z*, що відповідає межам вірогідного проміжку. Для цього обчислюємо значення функції Ф(z*) або Ф0(z*).
За таблицями значень функції Ф(z*) ([2] – табл.3 стор.304, [3] – прил.2 стр.297) або Ф0(z*) ([1] – табл.2 стор.192, [2] – табл.2 стор.303, [3] – прил.3 стр.299) знаходимо
Z*=1,96.
З формули півширини вірогідного проміжку виражаємо об’єм виборки n:
Підставляючи чисельні значення, знаходимо необхідний об’єм виробки
Приклад 7.3. Процентний вміст азоту в плазмі крові щурів вважають нормального розподіленою випадковою величиною. Визначити 95-відсотковий вірогідний проміжок для математичного сподівання на основі результатів дев’яти дослідів:
0,96;0,90;0,98;0,82;0,83;0,87;0,94;0,99;0,81.
Розв’язання. Оскільки дисперсія невідома і число елементів виборки невелике (менше 30), використовуємо статистику
Яка підпорядковується розподілу Стьюдента.
Розраховуємо вибіркове середнє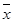
Де n – об’єм виборки, хi – і-й елемент виборки,
І стандартне відхилення 
Півширина (радіус) вірогідного проміжку визначається за формулою
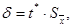
Де t * - коефіцієнт Стьюдента (значення нормованої змінної T, якому відповідає задане значення функції розподілу, яке визначається заданою надійною ймовірністю).
За таблицями розподілу Стьюдента ([1] – табл.6 стор.195, [2] – табл.6 стор.307, [3] – прил.4 стр.302.) визначаємо коефіцієнт Стьюдента (процентну точку розподілу), виходячи з числа ступенів свободи 
і рівня надійності 
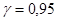(або рівня значущості 
)
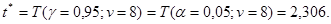
Зауваження. При визначенні коефіцієнта Стьюдента за таблицями слід мати на увазі, що одним з входів таблиці може бути або рівнем надійності 
([2] табл.6 стр.307, [3] прил.4 стр.302), або рівень значущості 
([1] табл.6 стор.195, [3] прил.5 стр.302.), які пов’язані між собою залежністю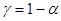 
Півширина (радіус) вірогідного проміжку дорівнює
Таким чином, істинне значення ознаки з надійністю 0,95 знаходиться у проміжку [0,844;0,936].
Приклад 7.4. В результаті вимірювання вмісту фосфору в лікарській рослині Y та вмісту фосфору в грунті Х отримано такі дані:
| Х | |||||||||
| Y |
1) Встановити, чи існує залежність між вмістом фосфору у грунті і вмістом фосфору у рослині.
2) Якщо залежність існує, знайти рівняння, яке її описує.
Розв’язання. Для встановлення наявності залежності між двома ознаками Х та Y за набором їх значень застосовується 1-факторний кореляційний аналіз.
З вигляду кореляційного поля можна зробити припущення, що між ознаками X та Y існує лінійна залежність, оскільки експериментальні точки групуються навколо прямої лінії. Наявність та тісноту лінійного зв’язку між яка підпорядковується розподілу Стьюдента з числом ступенів свободи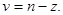 
Розраховуємо експериментальне значення статистики T:
Задаючись рівнем значущості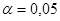 
(відповідний рівень надійності 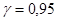) враховуючи, що критична область є однобічною, визначаємо за таблицями розподілу Стьюдента ([2] – табл.5 стор.306.) критичне значення статистики T
Оскільки експериментальне значення Т-статистики більше за критичне (Te>T*), то на рівні значущості 0,05 отримане значення коефіцієнта лінійної кореляції R слід вважати істотним.
Отже, на рівні значущості 0,05 (тобто з надійністю 0,95)можна твердити, що між ознакою Х (вміст фосфору у грунті) та ознакою Y (вміст фосфору у рослині) існує сильний прямий лінійний кореляційний зв’язок.
Лінійний зв’язок ознак X та Y описується лінійним рівнянням регресії
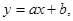
де a, b – коефіцієнти регресії, які визначаються методом найменших квадратів за формулами
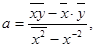
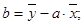
де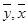 
- вибіркові середові ознак Y та X відповідно, 
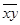- середнє значення добутку відповідних вибіркових значень ознак, 
- середнє значення квадрату ознаки Х.
Обчислення за цими формулами також зручно виконувати за допомогою розрахункової таблиці:
Двома ознаками визначають за допомогою коефіцієнта лінійної кореляції (коефіцієнта кореляції Пірсона) R, який розраховується за формулою
Де n - об’єм виборки,
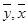- і-й елемент виборки { Xn }, {Yn} відповідно.
Обчислення за наведеною формулою зручно виконувати за допомогою введеної нижче розрахункової таблиці, які містить проміжні результат і відображає послідовність розрахунків.
| X | Y |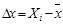 
| 
| 
| 
| 
|
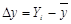
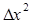
| -8 | -16 | |||||
| -9 | -9 | |||||
| -10 | -26 | |||||
| -6 | -9 | |||||
| -2 | -4 | |||||
|
| 
| 
| 
| 
| ||
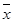
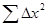
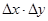
| R= | 0,90969 |
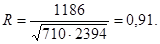
Істотність виявленого кореляційного зв’язку перевіряється за допомогою статистики
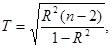
| X | Y | X2 | X*Y |
|
|
|
|
|
| 247,8889 | 1171,77 | ||
| a= | 1,670423 | ||
| b= | 58,28451 |
Підставляючи до формул коефіцієнтів регресії чисельне значення, знаходимо:
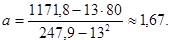
Отже рівняння регресії Y та X є
Остаточно з результатів кореляційно-реляційного аналізу можна з надійністю 95% зробити наступний висновок: між вмістом фосфору у грунті X і вмістом фосфору у рослині Y існує сильний прямий кореляційний зв’язок який записується рівнянням
