М К Э
Лекция 1. Метод Галёркина
Об ортогональности функций
Пусть  ‑ область изменения
‑ область изменения 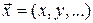 , а
, а  ‑ функции, определенные в
‑ функции, определенные в  . Через
. Через  обозначим класс этих функций.
обозначим класс этих функций.
а) Если  . Обозначение:
. Обозначение:  .
.
б) Пусть  ‑ полная в
‑ полная в  система базисных функций. Тогда любая функция
система базисных функций. Тогда любая функция  представима в виде разложения по базису
представима в виде разложения по базису
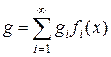 ,
,
где коэффициенты  определяются однозначно. Базисные функции линейно независимы, т.е. из равенства
определяются однозначно. Базисные функции линейно независимы, т.е. из равенства  следует, что все коэффициенты
следует, что все коэффициенты  равны нулю. Но тогда и
равны нулю. Но тогда и  . Итак, если функция ортогональна системе базисных функций, то она тождественно равна нулю.
. Итак, если функция ортогональна системе базисных функций, то она тождественно равна нулю.
Метод взвешенных невязок
Рассмотрим уравнение
 . (1.1)
. (1.1)
Пусть  ‑ приближение к решению
‑ приближение к решению  уравнения (1). Обозначим через
уравнения (1). Обозначим через
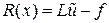 (1.2)
(1.2)
невязку уравнения (1) на этом приближенном решении. Пусть, далее,  ‑ система базисных функций. Тогда можно записать
‑ система базисных функций. Тогда можно записать
 .
.
Чтобы найти коэффициенты 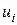 , потребуем, чтобы невязка
, потребуем, чтобы невязка  была ортогональна некоторой системе весовых функций
была ортогональна некоторой системе весовых функций  , т.е.
, т.е.
 (1.3)
(1.3)
Метод Галеркина
Галеркин использовал базисные функции вместо весовых, что приводит к следующей системе линейных уравнений относительно искомых коэффициентов разложения 

или
 (1.4)
(1.4)
Замечание. В конечномерном пространстве  , и система уравнений (4) становится конечной.
, и система уравнений (4) становится конечной.
Пример применения метода Галеркина.
Решим задачу
 (1.5)
(1.5)
Точное решение этой задачи очевидно:  . Выберем систему базисных функций
. Выберем систему базисных функций
 (1.6)
(1.6)
и запишем решение в виде разложения по базису,
 . (1.7)
. (1.7)
В разложении (7) искомыми являются коффициенты 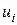 . Полагая
. Полагая  , находим
, находим  . Пусть
. Пусть  , тогда осталось найти
, тогда осталось найти  . Подставим (7) в (5) и вычислим невязку
. Подставим (7) в (5) и вычислим невязку
 .
.
Потребуем  . Получим систему уравнений
. Получим систему уравнений

Вычислим интегралы и получим

Решение этой системы таково: 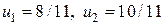 , а приближенное решение (7) задачи (5) есть парабола
, а приближенное решение (7) задачи (5) есть парабола
 .
.
График этой функции в сравнении с точным решением  показан на рисунке
показан на рисунке

Базисные функции с кончным носителем
До сих пор мы рассматривали базисные функции, определенные всюду в  . Часто такой выбор неудобен; напимер при выборе
. Часто такой выбор неудобен; напимер при выборе  при большом
при большом  получаются полиномы высокого порядка, что затрудняет вычисления. В МКЭ обычно применяют базисные функции с конечным носителем, который связан с триангуляцией области, т.е. с ее сеточным разбиением на конечные элементы. Рассмотрим простейший пример равномерной сетки на отрезке
получаются полиномы высокого порядка, что затрудняет вычисления. В МКЭ обычно применяют базисные функции с конечным носителем, который связан с триангуляцией области, т.е. с ее сеточным разбиением на конечные элементы. Рассмотрим простейший пример равномерной сетки на отрезке  с узлами
с узлами  Для каждого узла определим т.н. пирамидальную базисную функцию
Для каждого узла определим т.н. пирамидальную базисную функцию
 (1.8)
(1.8)

Заметим, что
 (1.9)
(1.9)
Поэтому, во-первых, такая система базисных функций линейно-независима, а во-вторых, коэффициенты разложения (7) любой функции по этому базису будут равны значениям функции в узлах сетки,  .
.
Лекция 2. Слабая (обобщенная) форма постановки краевых задач для дифференциальных уранений
Пусть  ‑ дифференциальный оператор, и требуется решить задачу
‑ дифференциальный оператор, и требуется решить задачу  . Умножим это уравнение на произвольную пробную функцию
. Умножим это уравнение на произвольную пробную функцию 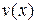 и проинтегрируем по области
и проинтегрируем по области  . Получим
. Получим
 (2.1)
(2.1)
Это уравнение должно выполняться  . Оно называется слабой формой исходного дифференциального уравнения. Идейно слабая форма (2.1) связана с подходом Галеркина или методом взвешенных невязок, поскольку может быть представлена в виде
. Оно называется слабой формой исходного дифференциального уравнения. Идейно слабая форма (2.1) связана с подходом Галеркина или методом взвешенных невязок, поскольку может быть представлена в виде
 .
.
Часто при записи обобщенных формулировок задач вместот интегралов используют эквивалентный символ скалярного произведения:
 (2.2)
(2.2)
Чтобы получить из (2.1) или (2.2) систему уравнений для узловых значений, достаточно
1) провести триангуляцию области;
2) выбрать ассоциированную с триангуляцией конечную систему базисных функций, обладающую свойством (9);
3) записать метод Галеркина (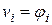 )
)
 (2.3)
(2.3)
или
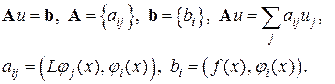 (2.4)
(2.4)
Пример использования базисных функций с конечным носителем.
Решим задачу теплопроводности
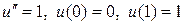 . (2.5)
. (2.5)
Точное решение задачи (2.5)  . Введем сетку
. Введем сетку
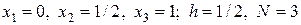 ;
;
выберем пирамидальные базисные функции (1.8) и подсчитаем их производные:
 (2.6)
(2.6)
Используя представление приближенного решения
 (2.7)
(2.7)
и граничные условия в точках  и
и  , получаем
, получаем

Таким образом, осталось найти коэффициент  . Для этого достаточно определить вторую строку системы уравнений (2.4), а именно коэффициенты
. Для этого достаточно определить вторую строку системы уравнений (2.4), а именно коэффициенты  . Непосредственное применение формул (2.4) для вычисления
. Непосредственное применение формул (2.4) для вычисления  невозможно, поскольку предполагает вычисления вторых производных от линейных базисных функций (2.6). Это отражает очевидный факт, что линейные функции не могут служить базисом в классе дважды дифференцируемых функций, которому принадлежит решение исходной дифференциальной задачи. Однако если ослабить требование гладкости, то с помощью формулы интегрирования по частям можно записать
невозможно, поскольку предполагает вычисления вторых производных от линейных базисных функций (2.6). Это отражает очевидный факт, что линейные функции не могут служить базисом в классе дважды дифференцируемых функций, которому принадлежит решение исходной дифференциальной задачи. Однако если ослабить требование гладкости, то с помощью формулы интегрирования по частям можно записать
 (2.8)
(2.8)
В правую часть формулы (2.8) теперь входят лишь первые производные базисных функций, которые определены в (2.6). При этом, несмотря на то, что производные терпят разрыв в узлах сетки, можно вычислить
 (2.9)
(2.9)
Заметим, что для интересующих нас коэффициентов 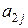 подстановка в правой части (2.9) равна нулю, т.к.
подстановка в правой части (2.9) равна нулю, т.к.  . Окончательно при
. Окончательно при  получим формулу
получим формулу
 (2.10)
(2.10)
Подставляя в (2.10) нужные значения производных из (2.6), найдем 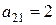 ,
,  ,
,  . Правая часть уравнения вычисляется интегрированием
. Правая часть уравнения вычисляется интегрированием
 .
.
Итак, второе уравнение системы уравнений для определения коэффициентов разложения имеет вид
 . (2.11)
. (2.11)
Нетрудно видеть, что уравнение (2.11) совпадает с конечно-разностной аппроксимацией исходного уравнения в центральном узле сетки.
Ранее с помощью граничных условий было установлено, что  , так что из (2.11) легко найти
, так что из (2.11) легко найти  . Окончательно приближенное решение задачи методом Галёркина имеет вид
. Окончательно приближенное решение задачи методом Галёркина имеет вид
 .
.
На рисунке показан график этой функции в сравнении с точным решением  .
.





