Нехай функція задана параметрично
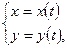
При чому  диференційовані при певних t, а
диференційовані при певних t, а  має обернену функцію. Тоді похідна від функції y по змінній x находиться за формулою
має обернену функцію. Тоді похідна від функції y по змінній x находиться за формулою
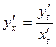
Диференціювання неявно заданої функції однієї змінної.
Неявна форма запису закону функціональної залежності однієї змінної має вигляд  .
.
Щоб знайти похідну неявної функції, можна взяти похідну від обох частин рівності  , вважаючи у функцією від х, і здобуте рівняння розв'язати відносно у'.
, вважаючи у функцією від х, і здобуте рівняння розв'язати відносно у'.
2. Дослідження функцій із застосуванням похідної. Побудова графіків функцій Асимптотою кривої називають пряму, до якої необмежено наближається точка кривої при необмеженому віддаленні ії від початку координат. Розрізняють вертикальні, похилі та горизонтальні асимптоти.
Вертикальною асимптотою графіка функції у=f(x) називають пряму х=х0, коли  або
або 
Похилою асимптотою графіка функції у=f(x) при 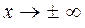 називають пряму у=kx+b, якщо існують границі
називають пряму у=kx+b, якщо існують границі 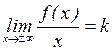 ,
, 
Горизонтальною асимптотою графіка функції у=f(x) при 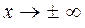 називають пряму у=b, коли
називають пряму у=b, коли 
Побудова графіків функцій
Побудову графіка функції у=f(x) пропонується проводити за такою схемою:
1. Визначають область визначення функції, області неперервності, точки розриву, точки перетину графіка функції з осями координат.
2. Якщо функція парна (f(-x)=f(x)) для будь-якого х або непарна (f(-x)=-f(x)), тоді базисний графік будують на [0,  ]. Для побудови повного графіка достатньо базисний графік симетрично відобразити відносно осі Оу у випадку парної функції або початку координат – у випадку непарної функції.
]. Для побудови повного графіка достатньо базисний графік симетрично відобразити відносно осі Оу у випадку парної функції або початку координат – у випадку непарної функції.
3. Знаходять асимптоти графіка функції.
4. Знаходять проміжки спадання та зростання функції, точки екстремуму.
5. Після виконання викладеного будують графік функції в цілому.
Дослідимо функцію  , притримуючись даної схеми.
, притримуючись даної схеми.
1.Областю визначення функції є  , х=4– точка розриву. Точки перетину з віссю ОX: y =0, х =-3; з віссю OY: х =0, y =-2,25.
, х=4– точка розриву. Точки перетину з віссю ОX: y =0, х =-3; з віссю OY: х =0, y =-2,25.
2. Функція не є ані парною, ані непарною. Графік симетрії немає.
3. Легко знаходимо, що х=4 – вертикальна асимптота, причому:
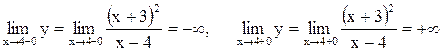
Знаходимо похилі асимптоти:

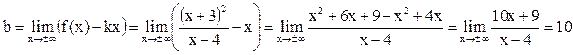
Таким чином, існує похила асимптота у=х+10.
4. Досліджуємо функцію на монотонність та локальний екстремум:

З  =0 слідує х2-8х-33=0, звідки х1=11, х2=-3. В інтервалі
=0 слідує х2-8х-33=0, звідки х1=11, х2=-3. В інтервалі 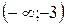
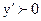 , отже, функція зростає в цьому інтервалі; в інтервалі (-3;4)
, отже, функція зростає в цьому інтервалі; в інтервалі (-3;4)  , отже функція спадає. Тому функція в точці х=-3 має локальний максимум: max(-3;0). В інтервалі (4;11)
, отже функція спадає. Тому функція в точці х=-3 має локальний максимум: max(-3;0). В інтервалі (4;11)  , отже функція спадає в цьому інтервалі; в інтервалі (11;
, отже функція спадає в цьому інтервалі; в інтервалі (11; 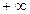 )
) 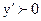 , отже функціязростає. В точці х=11 маємо локальний мінімум: min (11;28).
, отже функціязростає. В точці х=11 маємо локальний мінімум: min (11;28).
5. Графік функції зображено на рисунку 15.1.

Рисунок 15.1
3. Використання похідної при розв’язанні оптимізаційних задач
1. Серед прямокутників з даним периметром 2 p знайти той, площа якого найбільша.
Розв’язання. Нехай x – одна із сторін прямокутника, тоді друга p – x. Площа прямокутника S (x)= x (p – x). Функція S (x) має найбільше значення на [0, p ], оскільки є неперервною. Знаходимо S ′(x)= p –2 x. Перша похідна перетворюється на нуль при  . Оскільки S ″(x)=–2, тобто від’ємна при всіх значеннях x, то при
. Оскільки S ″(x)=–2, тобто від’ємна при всіх значеннях x, то при  функція має найбільше значення. Шуканий прямокутник – квадрат.
функція має найбільше значення. Шуканий прямокутник – квадрат.
2. Треба виготовити відкритий циліндричний резервуар об’ємом V. Вартість матеріалу, який іде на виготовлення дна, у m разів більша за вартість матеріалу для бічної частини. При яких розмірах резервуара вартість матеріалу буде найменшою?
Розв’язання. Нехай вартість матеріалу для бічної частини – одиниця, тоді вартість затрачених матеріалів на весь циліндр  , де R і h – відповідно радіус і висота резервуара. Застосовуючи формулу об’єму резервуара
, де R і h – відповідно радіус і висота резервуара. Застосовуючи формулу об’єму резервуара  , знаходимо
, знаходимо  . Цей вираз висоти підставимо у формулу для визначення вартості матеріалів
. Цей вираз висоти підставимо у формулу для визначення вартості матеріалів  . Знайдемо похідну по R і прирівняємо її до нуля:
. Знайдемо похідну по R і прирівняємо її до нуля:
 , тому
, тому  .
.
Легко помітити, що друга похідна  , S має найменше значення для визначеного R. Далі знайдемо
, S має найменше значення для визначеного R. Далі знайдемо
 .
.
Таким чином, вартість матеріалу для резервуару буде мінімальною, якщо висота циліндра у m разів перевищуватиме радіус його основи.
Лекція 16 Інтеграл. Інтегрування частинами
1. Невизначений інтеграл
Функція F(х) називається первісною для функції f(х) на відрізку [а,b], якщо F(х) диференційована на цьому відрізку і стверджується рівність F'(х) = f(х) для усіх  Існує множина первісних F(х) для однієї і той самої функції f(x) на даному відрізку. Усі вони можуть відрізнятись тільки сталою. Цю множину первісних називають невизначеним інтегралом від функції f(x) і записується
Існує множина первісних F(х) для однієї і той самої функції f(x) на даному відрізку. Усі вони можуть відрізнятись тільки сталою. Цю множину первісних називають невизначеним інтегралом від функції f(x) і записується 
2. Інтегрування частинами
Застосування формули  і знаходження первісної
і знаходження первісної
називається інтегруванням за частинами. До інтегрування за частинами відносяться випадки, коли підінтегральний вираз має вигляд:
1. 
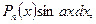


через и позначаємо Р п (х), через dv позначаємо соs ах dх, 
2. 


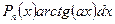
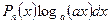

через и позначаємо  ,
,  ,
,  ,
,  ,
,  ,
,  , через dv позначаємо Рп(х)dх.
, через dv позначаємо Рп(х)dх.
При інтегруванні частинами, треба підінтегральний вираз розбити на два множника: и і dv. При цьому dv повинен бути таким, щоб інтегруванням легко було знайти v (сталу інтегрування беремо за 0).
3. Формула Ньютона - Лейбніца
Визначений інтеграл можна обчислити за формулою Ньютона – Лейбніца

Формула показує, що значення інтеграла на відрізку [а,b] дорівнює різниці значень первісної підінтегральної функції при верхній і нижній межах інтегрування.
Якщо функції и(х) і v(х) та їх похідні и'(х) і v'(х) неперервні на проміжку [а,b], то формула інтегрування за частинами для визначенного інтеграла має вигляд:

4. Знаходження інтегралів виду 
 ;
; 
Нагадаємо спочатку деякі формули, відомі з курсу математики
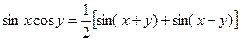 ; (16.1)
; (16.1)
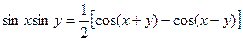 ; (16.2)
; (16.2)
 ; (16.3)
; (16.3)
 ; (16.4)
; (16.4)
 ; (16.5)
; (16.5)
Приклади. Обчислити інтеграли.
1.  .
.
Розв’язання. Використовуємо формулу (16.2):
 .
.
Відповідь:  .
.
2.  .
.
Лекція 17 Задачі, які приводять до диференціальних рівнянь. Диференціальні рівняння з відокремлюваними змінними, лінійні диференціальні рівняння першого порядку
1 Задачі, які приводять до диференціальних рівнянь
Приклад 1. З деякої висоти кинули тіло, маса якого  . Треба встановити, за яким законом буде змінюватися швидкість
. Треба встановити, за яким законом буде змінюватися швидкість  падіння цього тіла, якщо на нього крім сили тяжіння, діє сила опору повітря, пропорційна швидкості (з коефіцієнтом пропорціональності
падіння цього тіла, якщо на нього крім сили тяжіння, діє сила опору повітря, пропорційна швидкості (з коефіцієнтом пропорціональності  ). Тобто треба знайти
). Тобто треба знайти  .
.
Розв’язування: за другим законом Ньютона
 |



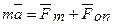












Рисунок 17.1
де 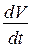 є прискорення тіла,
є прискорення тіла,  сила, яка діє на тіло в напрямку руху. Ця сила
сила, яка діє на тіло в напрямку руху. Ця сила  складається з двох сил: сили
складається з двох сил: сили  і сили опору повітря
і сили опору повітря  (рис.17.1).
(рис.17.1).
Ми отримали рівняння, яке зв’язує невідому функцію  та її похідну
та її похідну 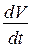 , тобто диференціальне рівняння відносно невідомої функції
, тобто диференціальне рівняння відносно невідомої функції  (це рівняння руху деяких парашутів). Розв’язати диференціальне рівняння – це значить знайти таку функцію
(це рівняння руху деяких парашутів). Розв’язати диференціальне рівняння – це значить знайти таку функцію  , яка разом зі своєю похідною задовольняє даному диференціальному рівнянню.
, яка разом зі своєю похідною задовольняє даному диференціальному рівнянню.
Приклад 2. Знайти таку криву, щоб тангенс кута нахилу дотичної в кожній точці чисельно дорівнював ординаті точки дотику (рис.17.2).







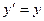


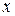
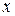
Рисунок 17.2
Приклад 3. Велике число популяції приведе до зменшення ресурсів, що знижує швидкість народження і підвищує швидкість вимирання.  - фундаментальне рівняння в демографічній математичній теорії поширення чутків, хвороб та інших проблемах фізіології та соціології.
- фундаментальне рівняння в демографічній математичній теорії поширення чутків, хвороб та інших проблемах фізіології та соціології.
Нехай функція  відображує кількісну сторону деякого явища. Дуже часто, коли розглядається це явище, ми не можемо встановити характер залежності
відображує кількісну сторону деякого явища. Дуже часто, коли розглядається це явище, ми не можемо встановити характер залежності  від
від 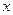 , але можемо встановити залежність між величинами
, але можемо встановити залежність між величинами 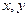 та похідними
та похідними 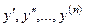 тобто написати диференціальне рівняння. З отриманої залежності між змінними
тобто написати диференціальне рівняння. З отриманої залежності між змінними 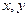 та похідними треба встановити безпосередню залежність
та похідними треба встановити безпосередню залежність  від
від 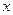 (знайти
(знайти  ), проінтегрувати диференціальне рівняння.
), проінтегрувати диференціальне рівняння.
Диференціальним рівнянням називається рівняння, яке зв’язує незалежну змінну  , шукану функцію
, шукану функцію  та її похідні
та її похідні 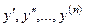 або диференціали. Символічно диференціальне рівняння записується
або диференціали. Символічно диференціальне рівняння записується
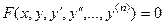
Порядком диференціального рівняння називається найвищий порядок похідної, що входить в диференціальне рівняння.
Наприклад рівняння  - першого порядку
- першого порядку
 - другого порядку
- другого порядку
 - третього порядку
- третього порядку
Процес знаходження розв’язку диференціального рівняння називається інтегруванням рівняння.
Розв’язком (або інтегралом) диференціального рівняння називається будь-яка функція  , визначена на деякому інтервалі (а; b), яка разом зі своїми похідними перетворює це рівняння у вірну тотожність. (При цьому похідні функції
, визначена на деякому інтервалі (а; b), яка разом зі своїми похідними перетворює це рівняння у вірну тотожність. (При цьому похідні функції  існують).
існують).
Приклад: Довести, що функція  , яка визначена на усій числовій прямій, є розв’язком диференціального рівняння
, яка визначена на усій числовій прямій, є розв’язком диференціального рівняння 






2 Диференціальні рівняння першого порядку: основні поняття, задача Коші
Диференціальним рівнянням першого порядку називається рівняння виду 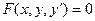
яке зв’язує незалежну змінну 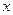 , шукану функцію
, шукану функцію  та її похідну
та її похідну  .
.
Якщо це рівняння можна розв’язати відносно  , то воно має нормальний вид:
, то воно має нормальний вид:

Умова  називається початковою умовою (
називається початковою умовою (
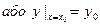 ).
).
Загальним розв’язком диференціального рівняння першого порядку називається функція  , яка залежить від
, яка залежить від 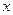 та однієї довільної сталої
та однієї довільної сталої  і задовольняє умовам:
і задовольняє умовам:
1.  задовольняє диференціальному рівнянню при довільному (конкретному) значенні
задовольняє диференціальному рівнянню при довільному (конкретному) значенні  .
.
2. Яка б не була початкова умова  , завжди можна знайти таке значення довільної сталої
, завжди можна знайти таке значення довільної сталої  , що функція
, що функція 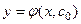 буде задовольняти початковій умові.
буде задовольняти початковій умові.
Частинним розв’язком диференціального рівняння називається розв’язок, який отримується з загального розв’язку при конкретному значенні довільної сталої  .
.
З геометричної точки зору загальний розв’язок  диференціального рівняння визначає на площині
диференціального рівняння визначає на площині  сім’ю інтегральних кривих.
сім’ю інтегральних кривих.
Задача знаходження частинного розв’язку диференціального рівняння за його загальним розв’язком при заданій початковій умові називається задачею Коші.
З геометричної точки зору розв’язати задачу Коші – це значить серед сім’ї інтегральних кривих вибрати ту одну, яка буде проходити через точку  .
.
3. Диференціальне рівняння з відокремлюваними змінними
Рівняння виду 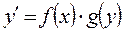 називається рівнянням з відокремлюваними змінними. Замінити
називається рівнянням з відокремлюваними змінними. Замінити  на
на  :
:  . Відокремити змінні
. Відокремити змінні  . Проінтегрувати обидві частини рівняння
. Проінтегрувати обидві частини рівняння 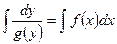 , G(y)=F(x)+C- загальний розв'язок.
, G(y)=F(x)+C- загальний розв'язок.
4. Лінійне диференціальне рівняння І порядку
Лінійним диференціальним рівнянням називається рівняння вигляду
 (17.1)
(17.1)
де  і
і  - задані функції.
- задані функції.
В окремому випадку  і
і  можуть бути сталими величинами.
можуть бути сталими величинами.
Це рівняння зводиться до рівняння з відокремлюваними змінними за допомогою підстановки  . Тоді
. Тоді  . Підставимо
. Підставимо  і
і  в (17.1). Маємо:
в (17.1). Маємо:

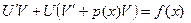 (17.2) Оскільки у виразі для
(17.2) Оскільки у виразі для  один множник можна вибрати довільно, а другий підібрати, то нехай
один множник можна вибрати довільно, а другий підібрати, то нехай  . Звідки знаходимо
. Звідки знаходимо 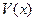 . З рівняння (17.2), підставляючи знайдений вираз
. З рівняння (17.2), підставляючи знайдений вираз  , знаходимо
, знаходимо 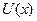 .
.
Загальний розв’язок записуємо у вигляді:

Приклад Розв’язати рівняння 

Лекція 18 Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами. Застосування диференціальних рівнянь до розв’язування
прикладних задач
Диференціальні рівняння другого порядку Рівняння виду  називається найпростішим диференціальним рівнянням другого порядку. Для розв’язання треба двічі проінтегрувати праву частину рівняння:
називається найпростішим диференціальним рівнянням другого порядку. Для розв’язання треба двічі проінтегрувати праву частину рівняння: 
 ;
;  - загальний розв'язок диференціального рівняння.
- загальний розв'язок диференціального рівняння.
Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтамиЛінійне однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами має вигляд: 
Складаємо характеристичне рівняння, для цього заміняємо
у" = к2; у' = к; у=1,
 .
.
Корені його характеристичного рівняння можуть бути:
1) дійсними і різними: 
2) дійсними і рівними: 
3) комплексно-спряженими:  .
.
Їм відповідають наступні загальні розв'язки рівняння
1) 
2) 
3) 
Застосування диференціальних рівнянь до розв’язування прикладних задач
Задача 1. Моторний човен рухається у спокійній воді зі швидкістю 1,5 м/с. Через 4с після вимкнення двигуна його швидкість зменшилась до 1 м/с. Враховуючи опір води пропорційний швидкості руху човна, знайти його швидкість через 50с після вимкнення двигуна.
Розв’язування:
Нехай  – швидкість човна після вимкнення двигуна в момент часу
– швидкість човна після вимкнення двигуна в момент часу  . Тоді залежність між
. Тоді залежність між  і
і  має вигляд
має вигляд  , де
, де  - маса човна.
- маса човна.

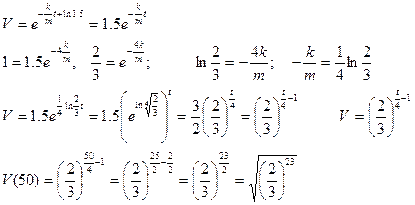
Задача 2
За 10 хвилин тіло охолоджується від 100о до 60о. Температура навколишнього повітря дорівнює 20о. Враховуючи, що швидкість охолодження тіла пропорційна різниці температур тіла і навколишнього повітря, визначити, за який час тіло охолоджується до 30о.
Розв’язування:
Нехай  - температура тіла у момент часу
- температура тіла у момент часу  . Тоді диференціальний закон охолодження тіла має вигляд:
. Тоді диференціальний закон охолодження тіла має вигляд:  .
.


Задача 3
Знайти рівняння кривої, що проходить через точку (а; а), якщо довжина відрізку осі абсцис, що відтинається її дотичною, дорівнює довжині цієї дотичної.
 |
у 
у 




 х x
х x
Рисунок 18.1
Розв’язування:
За геометричним змістом похідної  , де
, де 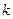 - кутовий коефіцієнт дотичної до графіка функції
- кутовий коефіцієнт дотичної до графіка функції  . З іншого боку,
. З іншого боку,  (рис.18.1)
(рис.18.1)
Отже,  .
.
Із 
За умовою задачі  .
.
Із 

Лекція 19 Числові ряди. Знакопостійні ряди. Необхідна та достатні ознаки
збіжності ряду
1 Поняття числового ряду. Основні означення
Нехай задана числова послідовність  .
.
Вираз  ,називається числовим рядом, а числа
,називається числовим рядом, а числа 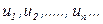 - членами ряду;
- членами ряду;  - загальний член ряду.
- загальний член ряду.
Сума Sn перших n членів ряду називається n-ю частковою сумою ряду:  .
.
Числовий ряд  називається збіжним, якщо послідовність його часткових сум збігається, тобто
називається збіжним, якщо послідовність його часткових сум збігається, тобто  , де число S називається сумою ряду.
, де число S називається сумою ряду. 
Якщо послідовність  не має скінченої границі, то ряд
не має скінченої границі, то ряд  називається розбіжним. Розбіжний ряд не має суми.
називається розбіжним. Розбіжний ряд не має суми.
Приклад. Показати, що ряд  збігається, і знайти його суму.
збігається, і знайти його суму.
 У цьому випадку
У цьому випадку 
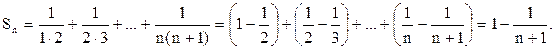 Тоді
Тоді  Даний ряд збігається і його сума S =1.
Даний ряд збігається і його сума S =1.
Розглянемо ряд  . При
. При 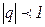 ряд збіжний і сума
ряд збіжний і сума  . При
. При  ряд розбіжний.
ряд розбіжний.
Розглянемо ряд 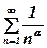 . При
. При  ряд збіжний. При
ряд збіжний. При  ряд розбіжний.
ряд розбіжний.
Основні властивості рядів
1 Якщо ряд  збігається, то ряд
збігається, то ряд  теж збігається і його сума дорівнює
теж збігається і його сума дорівнює 
2 Якщо збігаються ряди  і
і  , то ряд
, то ряд  теж збігається.
теж збігається.
2 Необхідна ознака збіжності ряду
Якщо ряд збігається, то послідовність його членів прямує до нуля, тобто  . Ця ознака є необхідною, але не є достатньою. Розглянемо гармонійний ряд, тобто ряд
. Ця ознака є необхідною, але не є достатньою. Розглянемо гармонійний ряд, тобто ряд  Хоча
Хоча  але ряд розбіжний. Якщо
але ряд розбіжний. Якщо  не існує або існує, але
не існує або існує, але  то ряд розбігається.
то ряд розбігається.
Приклад. Дослідити на збіжність ряд 
 тобто ряд розбіжний.
тобто ряд розбіжний.
3 Достатні ознаки збіжності знакододатніх рядів Будемо розглядати тільки знакододатні ряди, тобто ряди, в яких  Його часткові суми утворюють зростаючу послідовність. З теорії границь відомо, що монотонно зростаюча й обмежена зверху послідовність має границю.
Його часткові суми утворюють зростаючу послідовність. З теорії границь відомо, що монотонно зростаюча й обмежена зверху послідовність має границю.
Ознаки порівняння
1. Нехай маємо ряди
 (19.1)
(19.1)
 причому
причому  (19.2)
(19.2)
Тоді із збіжності більшого ряду (19.2) випливає збіжність меншого ряду (19.1), а з розбіжності меншого ряду (19.1) випливає розбіжність більшого ряду (19.2).
2. Якщо  то обидва ряди збіжні або розбіжні одночасно.
то обидва ряди збіжні або розбіжні одночасно.
Приклад 1 Дослідити на збіжність ряд:  .
.
Порівняємо з рядом  , який є збіжним
, який є збіжним  .
.  . Згідно першої ознаки порівняння ряд
. Згідно першої ознаки порівняння ряд 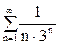 - збіжний.
- збіжний.
Приклад 2 Дослідити на збіжність ряд: 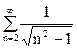 .
.
Порівняємо з рядом  -розбіжний.
-розбіжний.  . Згідно порівняння ряд
. Згідно порівняння ряд  - розбіжний.
- розбіжний.
Ознака Даламбера
Розглянемо ряд 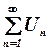 з додатними членами. Нехай існує границя
з додатними членами. Нехай існує границя  , тоді при
, тоді при  ряд збігається, а при
ряд збігається, а при  - розбігається. У випадку, коли
- розбігається. У випадку, коли  ознака не діє і нічого певного про збіжність ряду сказати не можна.
ознака не діє і нічого певного про збіжність ряду сказати не можна.
Приклад 1: Дослідити на збіжність ряд  . Маємо
. Маємо  Тоді за ознакою Даламбера:
Тоді за ознакою Даламбера:  даний ряд збіжний.
даний ряд збіжний.
Приклад 2: Дослідити на збіжність ряд:  . Маємо
. Маємо 
 . Тоді
. Тоді  ряд розбіжний.
ряд розбіжний.
Ознака Коші
Нехай для будь-якого  існує границя
існує границя  , то при
, то при  - ряд
- ряд 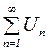 збігається, а при
збігається, а при  - розбігається. При
- розбігається. При  радикальна ознака Коші не застосовується.
радикальна ознака Коші не застосовується.
Приклад 1 Дослідити на збіжність ряд:  Для цього ряду
Для цього ряду  ряд збігається.
ряд збігається.
Приклад 2 Дослідити на збіжність ряд:  . Маємо
. Маємо  для цього ряду
для цього ряду  ряд розбігається.
ряд розбігається.
Список літератури
1. Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов.- 3-е изд., перераб. и доп. – М.: Высш. шк., 1990. – 495 с.
2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб. пособие.- 2-е изд. перераб.и доп.– М.: Наука, Гл. ред. физ.-мат. лит., 1989. – 576 с.
3. Математика для техникумов. Алгебра и начала анализа: Учебник Ч.2. Под ред. Г.Н. Яковлева - 3-е изд. перераб.– М.: Наука, Гл. ред. физ-мат. лит., 1988. – 272 с.
4. Овчинников П.П., Яремчук Ф.П., Михайленко В. М. Вища математика: Підручник. У 2 ч. Ч.1.-3-є вид., випр. – К.: Техніка, 2003. – 600с.
5. Пак В.В., Носенко Ю.Л. Вища математика: Підручник. – К.: Либідь, 1996. – 440с.






