Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция (рис.).
Если оси всех стержней фермы лежат в одной плоскости, то ее называют плоской фермой.
Точки, в которых сходятся оси стержней, называются узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами.
Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру – нижний пояс.
Вертикальные стержни называются стойками, а наклонные – раскосами.
Реакция каждого из опорных стержней направлена по оси этого стержня.
Способ вырезания узлов состоит в том, что мысленно вырезают узлы фермы и прикладывают к ним соответствующие внешние силы и реакции стержней и составляют уравнения равновесия сил, приложенных к каждому узлу. Условно предполагают, что все стержни растянуты (реакции направлены от узлов).
Последовательность рассмотрения узлов определяется обычно условием, что число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия сил (двух - для плоской фермы, трех – для пространственной). Тогда неизвестные силы определяются сразу из уравнений равновесия, действующих на узел.
Усилия в отдельных стержнях фермы могут оказаться равными нулю. Такие стержни принято называть нулевыми. Иногда их можно определить, не производя расчетов, пользуясь правилами:
- Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю.
- Если в незагруженном узле плоской фермы сходятся три стержня, два из которых располагаются на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых двух стержнях равны между собой.
- Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю приложенной силе, а усилие в другом стержне равно нулю.
Пример.1 Определить усилия в стержнях фермы (рис.5.11), если к узлу 
приложена вертикальная сила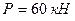 
. Т.к. 
Рис. 5.11
сила 
, приложенная к узлу фермы, и реакция шарнирно-подвижной опоры 
вертикальны, то линия действия шарнирно-неподвижной опоры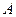 
должна быть им параллельна, т.е. тоже вертикальна. Тогда для трех параллельных взаимно уравновешивающихся сил 
имеем
,
откуда 
.
Для определения усилий в стержнях фермы рассматриваем равновесие сил, приложенных к каждому ее узлу в такой последовательности, чтобы число неизвестных сил в нем не превышало двух. Условно предполагаем, что все стержни растянуты, т.е. реакции стержней направлены от узлов.
Составим по два уравнения равновесия для каждого узла фермы.
Узел :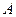
;
;
.
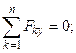
Узел 
:
;
;
.
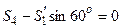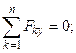
Узел
;
.
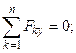
Узел 
:
;
;
.
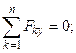
Узел :
;
.
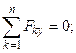
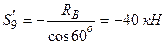По результатам расчетов составляем таблицу усилий в стержнях фермы.
| Стержни | |||||||||
| -80 | 69,2 | -69,2 | 34,6 | 34,6 | -40 |
Способ Риттера рассмотрим на конкретном примере.
Пример 2. Рассмотрим ферму, изображенную на рис.5.12. На ферму действуют вертикальные внешние силы: задаваемая сила 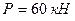и реакции опор 
.
Рис. 5.12
При определении усилий все стрежни фермы условимся считать растянутыми. Знак минус в ответе будет означать, что стержень сжат. Пусть требуется определить усилие в стержнях 6, 7, 8.
Проводим сечение, рассекая не более трех стержней. Мысленно отбрасываем левую часть фермы, заменяя ее действие на оставшуюся правую часть усилиями 
, направленными в сторону отброшенной части (рис.5.13). Чтобы определить усилие 
независимо от усилий 
и 
, составляем уравнение моментов сил, действующих на правую часть фермы, относительно точки 
, в которой пересекаются линии действия сил 
и 
. Эту точку называют точкой Риттера.
.
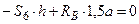Т.к. 
, то
.
Для определения усилия независимо от усилий и , спроецируем все силы, действующие на правую часть фермы, на вертикальную ось 
, т.к. проекции сил 
, на эту ось равны нулю:
Для определения усилия составим уравнение моментов этих же сил относительно точки Риттера 
, в которой пересекаются линии действия сил и :
; 
.
Знаки полученных ответов показывают, что стержень 6 растянут, а стержни 7 и 8 сжаты.
