Лекция №5. Распределенные силы. Заделка. Определение
Реакций опор составных конструкций. Ферма. Определение усилий в стержнях ферм.
Распределенные силы. Заделка.
Плоская система распределенных сил характеризуется интенсивностью, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка
.
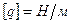1. 
Силы, равномерно распределенные вдоль отрезка прямой.
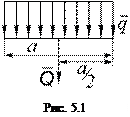Для такой системы сил интенсивность 
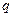имеет постоянное значение при статических расчетах ее можно заменить силой 
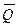, приложенной в середине отрезка и равной по модулю
.
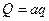2. 
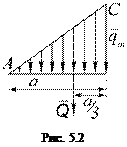Силы, распределенные вдоль отрезка прямой по линейному закону.
Примером такой нагрузки могут служить силы давления воды имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность 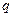является величиной переменной, растущей от нуля до максимального значения 
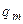. Равнодействующая 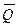таких сил определяется аналогично равнодействующей сил тяжести, действующих на треугольную пластину. Т.к. вес однородной пластины пропорционален ее площади, то
.
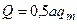Приложена сила 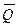на расстоянии 
от стороны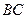 
.
3. Силы, равномерно распределенные по дуге окружности. Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндрического сосуда.
Пусть радиус дуги равен 
, 
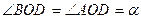, где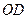 
- ось симметрии, вдоль которой направим ось 
. Действующая на дугу система сходящихся сил имеет равнодейст вующую 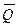, направленную в силу симметрии вдоль оси . При этом численно 
.
Для определения величины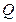 
выделим на дуге элемент, положение которого определяется углом 
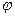, а длина 
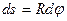. Тогда действующая на этот элемент сила численно равна 
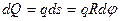, а проекция этой силы на ось будет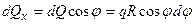 
. Тогда
.
Но из рис. видно, что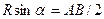 
. Следовательно, т.к. , то
,
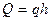где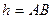 
- длина хорды, стягивающей дугу 
.
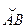4. Жесткая заделка (или неподвижная защемляющая опора) Заделанный конец балки и стену рассматривают как одно целое. На балку со стороны заделанного конца действует система распределенных сил. Приводя их к центру сечения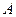 
их можно заменить одной силой 
и парой сил с моментом 
. Силу чаще всего раскладывают на составляющие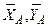 
, а момент считают положительным. Таким образом, для нахождения реакции заделки необходимо определить три величины , .
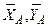Пример. Определить реакции заделки консольной балки, изображенной на рис., находящейся под действием сосредоточенной силы, пары сил и распределенной нагрузки, изменяющейся по закону треугольника и трапеции.
Изобразим реакции заделки 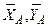, , разложим приложенную силу на две составляющие 
, тогда 
. Распределенную нагрузку заменим тремя силами: силой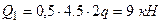 
, приложенной на расстоянии 
от заделки; силой 
, приложенной на расстоянии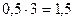 
от заделки; силой 
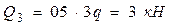, приложенной на расстоянии 
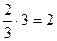от заделки. Запишем уравнения равновесия:
,
,
,
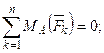
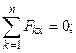
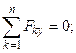
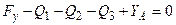откуда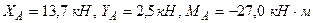 
.
