Если данная система имеет равнодействующую, то момент равнодействующей относительно любого центра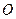 
равен сумме моментов сил системы относительно того же центра.
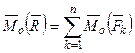(4.2)
▲ Пусть система сил приводится к равнодействующей 
, приложенной в точке 
. Приложим к этой точке силу 
. Тогда система 
~ 0, а, следовательно, должно выполняться равенство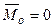 
:
, 
. ∆
Теорема об изменении главного момента при перемене центра приведения.
Главный момент при перемене центра приведения изменяется на момент главного вектора, приложенного в старом центре приведения, относительно нового центра приведения.
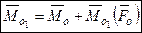(4.3)
▲ Главный вектор системы сил не зависит от центра приведения, поэтому
.
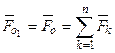Для центра приведения 
главный момент равен:
,
где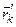 
- радиус вектор точки приложения силы 
, проведенный из нового центра приведения.
С учетом 
, получим:
∆
Статические инварианты. Динамический винт.
Согласно (4.3) главный момент для нового центра приведения определяется формулой:
Умножим обе части этого равенства скалярно на вектор 
:
Т.к. 
, то 
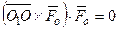, откуда 
.
Т.е. скалярное произведение главного вектора на главный момент не зависит от центра приведения.
Таким образом, при перемене центра приведения не изменяются главный вектор и скалярное произведение главного вектора на главный момент. Говорят, что эти величины инвариантны относительно выбора центра приведения.
Первым статическим инвариантом называется главный вектор .
.
Вторым статическим инвариантом называется скалярное произведение главного вектора на главный момент.
.
Совокупность силы и пары сил с моментом, коллинеарным силе, называется динамическим винтом или динамой. Другими словами динамический винт представляет собой совокупность силы и пары сил, действующей в плоскости, перпендикулярной силе.
Правый и левый динамические винты:
Рис. 4.5
Теорема о приведении к динаме.
Если второй статический инвариант не равен нулю, то систему сил можно привести к динаме.
Рис. 4.6а Рис. 4.6б
▲ Пусть в произвольной точке 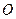система сил приведена к главному вектору и паре сил с моментом 
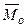. Т.к. 
, то 
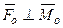. Разложим вектор главного момента на составляющие 
, так чтобы 
. Вектор 
представляет собой момент пары, расположенной в плоскости, перпендикулярной . Выберем силы пары 
таким образом, чтобы 
, приложим пару в точке 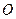. Т.к. система сил 
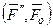~0, то их можно отбросить. А т.к. момент 
- свободный вектор, то его можно перенести в точку . Таким образом, заданная система сил приведена в точке к динамическому винту. ∆
