Главный вектор и главного момент пространственной системы сил.
Главным вектором системы сил называется сумма всех сил, действующих на данное тело.
.
Главным моментом системы относительно какого-либо полюса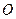 
называется сумма моментов всех сил относительно этого полюса.
.
Определим модули и направления векторов 
и 
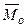. Выберем декартову систему координат таким образом, чтобы ее начало координат совпадало с центром приведения сил. Тогда
,
.
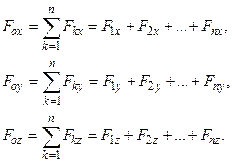
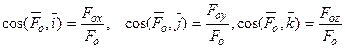Т.к.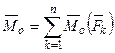 
, а
,
то
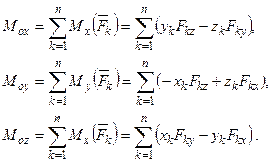
Следовательно, модуль и направление вектора 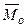определяются формулами:
,
.
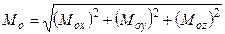Теорема о параллельном переносе силы.
Силу, приложенную к абсолютно твердому телу, можно переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.
▲ Пусть на твердое тело действует сила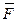 
, приложенная в точке 
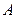. Действие этой силы не изменится, если к любой точке тела 
приложить уравновешенную систему 
сил 
, таких что 
. Полученную систему трех сил можно рассматривать как силу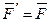 
, но приложенную в точке , и пару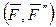 
с моментом 
. ∆
Теорема о приведении системы сил к простейшему виду.
Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру 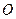, заменяется одной силой , равной главному вектору системы сил и приложенной в центре приведения 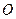, и одной парой с моментом 
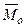, равным главному моменту системы относительно центра .
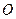Рис. 4.2
▲ Пусть на тело действует система сил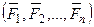 
. Перенесем все силы в центр . Тогда на тело будет действовать система сил
,
приложенных в центре и система пар, моменты которых равны
.
Сходящиеся силы, приложенные в точке , заменяются одной силой , приложенной в точке . Чтобы сложить все пары нужно сложить векторы моментов этих пар. В результате система пар заменится одной парой с моментом :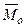
, 
.
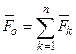Условия равновесия системы сил.
Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор системы сил и ее главный момент относительно любого центра были равны нулю.
, 
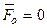. (4.1)
▲ Условия (4.1) являются необходимыми, т.к. если какое либо из них не выполняется, то система сил приводится или к равнодействующей (если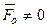 
) или к паре сил (если 
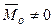). Условия (1) являются достаточными, т.к. при 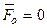система сил может приводиться только к паре с моментом 
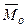, а т.к. 
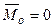, то равновесие выполняется. ∆
Частные случаи равновесия плоской системы сил.
Для равновесия плоской системы необходимо и достаточно, чтобы:
1.суммы проекций всех сил на каждую из координатных осей и сумма моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.
.
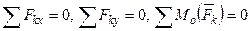2. суммы моментов всех этих сил относительно каких-нибудь двух центров 
и 
, и сумма их проекций на ось 
, не перпендикулярную прямой 
, были равны нулю.
.
3. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов этих сил относительно любых трех центров 
, не лежащих на одной прямой, были равны нулю.
.
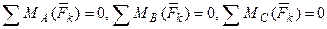