Кинематическое силовое исследование механизма.
Определение геометрических размеров звеньев механизма.
По заданному коэффициенту k определяем угол  :
:
 .
.
По известной величине Н (ход ползуна) определяем  ;
;
 .
.
Для положения рабочего хода 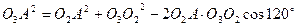 ,
,
 мм.
мм.
Для положения холостого хода  мм.
мм.
Из соотношения  найдем
найдем 
 .
. 
 .
.
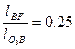 , следовательно
, следовательно 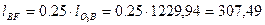
 .
.
 , следовательно
, следовательно 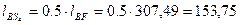
 .
.
Структурный анализ кулисного механизма.
Примем следующие обозначения звеньев механизмов: О – стойка, 1- кривошип  , 2 – камень А кулисы, 3 – кулиса
, 2 – камень А кулисы, 3 – кулиса  , 4 – шатун BF, 5 – ползун F.
, 4 – шатун BF, 5 – ползун F.
Количество подвижных звеньев n=5.
Кинематические пары: 1) стойка - кривошип  , 2) кривошип
, 2) кривошип  - камень А, 3) камень А - кулиса
- камень А, 3) камень А - кулиса  , 4) кулиса
, 4) кулиса  - стойка, 5) кулиса
- стойка, 5) кулиса  - шатун BF, 6) шатун BF - ползун F, 7) ползун F – стойка.
- шатун BF, 6) шатун BF - ползун F, 7) ползун F – стойка.
Количество кинематических пар пятого класса  . Степень подвижности механизма
. Степень подвижности механизма  .
.
Структурные группы механизма: 1) стойка – кривошип  - механизм I класса, I порядка по Артоболевскому, I класса, I порядка по Ассуру. 2)камень А – кулиса
- механизм I класса, I порядка по Артоболевскому, I класса, I порядка по Ассуру. 2)камень А – кулиса  - группа II класса, II порядка по Артоболевскому и по Ассуру. 3) шатун
- группа II класса, II порядка по Артоболевскому и по Ассуру. 3) шатун  - ползун
- ползун  - группа II класса, II порядка по Артоболевскому; I класса, II порядка по Ассуру. Механизм относится к II классу, II порядку по Артоболевскому; I классу, II порядку по Ассуру.
- группа II класса, II порядка по Артоболевскому; I класса, II порядка по Ассуру. Механизм относится к II классу, II порядку по Артоболевскому; I классу, II порядку по Ассуру.

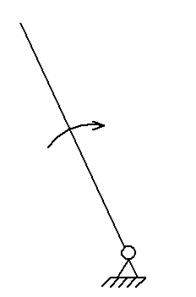
Рисунок 1 − Механизм поперечно-строгального станка

n=2
p5=3
W=0
II класс, II порядок по Артоболевскому
Iкласс, II порядок по Ассуру

n=2
p5=3
W=0
II класс, II порядок по Артоболевскому
II класс, II порядок по Ассуру
W=1
I класс, I порядок по Артоболевскому
Iкласс, I порядок по Ассуру
Рисунок 2 − Структурный анализ механизма
Кинематическое исследование шестизвенного механизма.
Планы механизма. Строим механизм (масштаб 1:2.5) (лист I). Строим планы механизма, начиная с построения положений ведущего звена – кривошипа  . Кривошип изображается в 15 положениях (в приложении на листе I указаны два положения механизма – рабочего и холостого хода).
. Кривошип изображается в 15 положениях (в приложении на листе I указаны два положения механизма – рабочего и холостого хода).
Рабочий ход.
План скоростей.
Угловая скорость вращения кривошипа 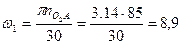
 .
.
Скорость точек  определяем по формуле
определяем по формуле  . Пусть
. Пусть 
 .
. 

 .
.
Масштаб плана скоростей  .
.
Скорость точки  определяем графическим решением уравнения
определяем графическим решением уравнения  ,
,  ||
|| 
 ,
,  ,
, 

 .
. 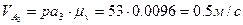 .
.
Угловая скорость звена 

 .
.
Ускорение Кориолиса  . Обозначим направление ускорения Кориолиса, для чего повернем вектор
. Обозначим направление ускорения Кориолиса, для чего повернем вектор 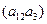 по направлению угловой скорости на 90°.
по направлению угловой скорости на 90°.
Скорость точки В найдем по формуле  ,
,
 - откладываем на плане скоростей.
- откладываем на плане скоростей.
Чтобы определить скорость точки F, воспользуемся векторным уравнением:  , bf
, bf  BF.
BF.
 , следовательно
, следовательно  .
.
Скорость центров масс 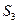 кулисы 3 находим по теореме о подобии
кулисы 3 находим по теореме о подобии 
 ,
,  .
.
План ускорений.
Ускорение точки А1 и А2 найдем по формуле 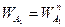 ,
, 
 . Пусть
. Пусть  .
.
Масштаб ускорений 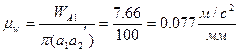 .
.

 , соответственно
, соответственно 
 ,
, 
 .
.
Решим графически уравнения  ,
, 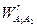

 ,
,
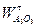

 ,
,  .
.
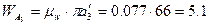
 .
.
Угловое ускорение звена 
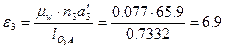
 .
.
Ускорение точки В определяем на основании теоремы о подобии 
 ,
, 
 .
.
Ускорение точки F определяем графическим построением уравнения  ,
,  ||
||  .
.

 , следовательно
, следовательно 
 .
.
Ускорение центров масс 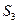 кулисы 3 находим по теореме о подобии
кулисы 3 находим по теореме о подобии 
 . Следовательно,
. Следовательно, 
 .
.
2.3.2 Холостой ход.
План скоростей.
Угловая скорость вращения кривошипа  .
.
Скорость точек  определяем по формуле
определяем по формуле  . Пусть
. Пусть 
 .
. 

 .
.
Масштаб плана скоростей  .
.
Скорость точки  определяем графическим решением уравнения
определяем графическим решением уравнения  ,
, 

 ,
,
 ,
,  ,
,  ||
||  .
. 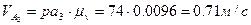 .
.
Угловая скорость звена 

 .
.
Ускорение Кориолиса  .
.
Скорость точки В найдем по формуле  .
.

Чтобы определить скорость точки F, воспользуемся условием, что  ||хх и векторным уравнением:
||хх и векторным уравнением:  , bf
, bf  BF.
BF.
 , следовательно
, следовательно 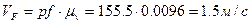 .
.
Скорость центров масс 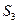 кулисы 3 находим по теореме о подобии
кулисы 3 находим по теореме о подобии 
 ,
,  .
.
План ускорений.
Ускорение точки А1 и А2 найдем по формуле 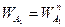 ,
,

 . Пусть
. Пусть  .
.
Масштаб ускорений  .
.
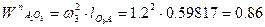
 , соответственно
, соответственно  определяем как
определяем как 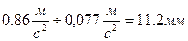 .
. 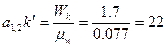
 .
.
Решим графически уравнения 
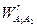


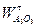

 ,
,  .
.
 .
.
Угловое ускорение звена 
 .
.
Ускорение точки В определяем на основании теоремы о подобии 
 ,
, 
 .
.
Ускорение точки F определяем графическим построением уравнения  ,
,  ||
||  .
.
 . Следовательно,
. Следовательно, 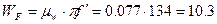
 .
.
Ускорение центра масс 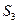 кулисы 3 находим по теореме о подобии
кулисы 3 находим по теореме о подобии 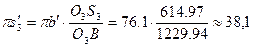
 . Следовательно,
. Следовательно, 
 .
.
Таблица 1 − Величины отрезков, мм, изображающих в масштабе  скорости точек звеньев механизмов
скорости точек звеньев механизмов
| отрезок | Значение в положении | |
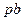
| 87.5 | 156.3 |

| 155.5 | |
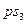
| 43.75 | 78.2 |

| ||

| 1229.94 | |

| 733.2 | 598.17 |
Таблица 2 − Величина угловой скорости кулисы
| Параметр | Значение в положении | |
 , рад/с , рад/с
| 0.68 | 1.2 |
Таблица 3 − Величины отрезков, мм, изображающих в масштабе  ускорения точек звеньев механизмов
ускорения точек звеньев механизмов
| Отрезок | Значение в положении | |

| 111.6 | 76.1 |

| 64.2 | 70.2 |

| 55.8 | 38.1 |
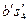
| 32,1 | 35,1 |

| ||

| 1229.94 | |

| 733.2 | 598.17 |
Таблица 4 − Величины отрезков, мм, изображающих в масштабе  нормальное ускорение
нормальное ускорение
| Параметр | Значение в положении | |
 , , 
| 0.34 | 0.86 |
Таблица 5 − Величины скоростей и ускорений характерных точек механизма
| Параметр | Значение в положении | |
 , , 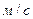
| 0.86 | 0.86 |
 , , 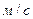
| 0.5 | 0.71 |
 , , 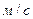
| 0.42 | 0.75 |
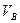 , , 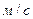
| 0.84 | 1.5 |
 , , 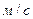
| 0.84 | 1.5 |
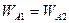 , , 
| 7.66 | 7.66 |
 , , 
| 5.1 | 2.9 |
 , , 
| 4.3 | |
 , , 
| 8.6 | 5.9 |
 , , 
| 13.5 | 10.3 |
Таблица 6 − Величины углового ускорения кулисы
| Параметр | Значение в положении | |
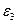 , , 
| 6.9 | 4.5 |
2.4 Кинетостатическое исследование шестизвенного механизма.
2.4.1 Определение результирующих сил инерции звеньев:
1.Кулисы 
Рабочий ход: 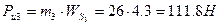 .
.
Холостой ход:  .
.
2.Ползуна  :
:
Рабочий ход:  .
.
Холостой ход:  .
.
2.4.2 Определение радиуса инерции:
кулисы 
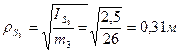 .
.
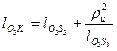
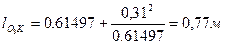
 ;
;
Определение сил тяжести звеньев.
Сила тяжести кривошипа  , где
, где 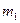 - масса зубчатого колеса 5.
- масса зубчатого колеса 5.
Массу 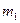 определяем через массу
определяем через массу  венца зубчатого колеса.
венца зубчатого колеса.
 ,
,  - диаметр окружности впадин колеса 5.
- диаметр окружности впадин колеса 5.
 .
.
S - площадь поперечного сечения венца колеса. Приняв ширину колеса равной b=40 мм и высоту сечения венца 
 , определим площадь сечения:
, определим площадь сечения:  .
.  - плотность материала колеса, считая, что колесо чугунное, принимаем
- плотность материала колеса, считая, что колесо чугунное, принимаем  .
.
 ;
;
 .
.
Сила тяжести:
Кулисы 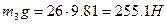 ;
;
Резцовой призмы  .
.
Рабочий ход.
Рассмотрим условия равновесия структурной группы, состоящей из ползуна 5 и шатуна 4.
 ;
;
 Н;
Н;
 ;
;
Следовательно, результирующая сила инерции  ;
;
Сила инерции  ;
;
Определяем масштаб построения плана сил 
 ;
;
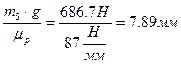 ;
;
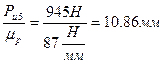
Силы  ,
,  найдем графически, построив план сил согласно уравнению
найдем графически, построив план сил согласно уравнению
 ;
;
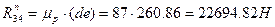 ;
;
Рассмотрим группу, состоящую из звеньев  и
и  .
.
Условие равновесия:  ;
;
Следовательно,
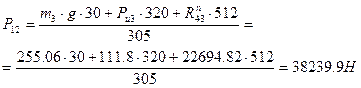
Определяем масштаб построения плана сил
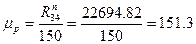
 ;
;

 ;
;

 ;
;

 ;
;
Силy 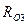 найдем графически, построив план сил согласно уравнению.
найдем графически, построив план сил согласно уравнению.
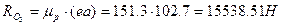 .
.
Рассмотрим равновесие ведущего звена – кривошипа  :
:
 ;
;
 ;
;
Следовательно, 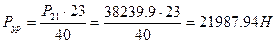 ;
;
Определяем масштаб построения плана сил

 ;
;

 .
.
Силy  найдем графически, построив план сил согласно уравнению.
найдем графически, построив план сил согласно уравнению.
 .
.
Холостой ход.
Рассмотрим условия равновесия структурной группы, состоящей из ползуна 5 и шатуна 4.
 ;
;
 Н;
Н;
Сила инерции  .;
.;
Определяем масштаб построения плана сил 
 ;
;
 ;
;
Силы  ,
,  найдем графически, построив план сил согласно уравнению
найдем графически, построив план сил согласно уравнению
 ;
;
 ;
;
Рассмотрим группу, состоящую из звеньев  и
и  .
.
Условие равновесия:  ;
;

Следовательно,

Определяем масштаб построения плана сил

 ;
;

 ;
;
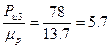
 ;
;
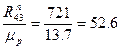
 ;
;
Силy 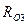 найдем графически, построив план сил согласно уравнению.
найдем графически, построив план сил согласно уравнению.
 .
.
Рассмотрим равновесие ведущего звена – кривошипа  :
:
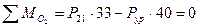 ;
;
 ;
;
Следовательно,  ;
;
Определяем масштаб построения плана сил 
 ;
;

 .
.
Силy  найдем графически, построив план сил согласно уравнению.
найдем графически, построив план сил согласно уравнению.
 .
.
Таблица 7 − Величины давлений в кинематических парах
| Параметр | Значение в положении | |

| 31075.97 | 836.43 |

| 38239.9 | 1368.38 |

| 15538.51 | 819.26 |

| 22694.82 | |
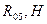
| 686.7 | 686.7 |
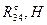
|
Рычаг Жуковского.
 ;
;
Следовательно, 
Погрешность  .
.
Аналогичным образом можно проверить рабочий ход.






