АЛГЕБРА
Инструкция: «Вам предлагаются задания с одним правильным ответом из пяти предложенных. Выбранный ответ необходимо отметить на листе ответов путем полного закрашивания соответствующего кружка».
1. Упростите выражение: (5a + b)·2b – 10ab
A)  B)
B)  C)
C)  D)
D)   E)
E) 
|
2. Найдите значение выражения:  A) – 1
B) 24
C) – 25
D) 25
E) 11
A) – 1
B) 24
C) – 25
D) 25
E) 11
|
3. Решите уравнение: 100х2 – 1= 0
A) 0; 0,01
B) 0; 0,1
C) 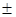 0,1
D) 0,1
D) 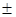 0,01
E) 0; – 0,1 0,01
E) 0; – 0,1
|
4. Решите уравнение: 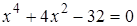 A) 2
B)
A) 2
B) 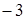 C)
C)  D)
D)  E)
E) 
|
5. Решите систему уравнений:  A) (–1; –2);
A) (–1; –2);  B) (2; 1);
B) (2; 1);  C)
C)  D) (
D) ( ; 4); (2; 1)
E) (3; 4); (4; ; 4); (2; 1)
E) (3; 4); (4;  ) )
|
| 6. Одновременно из двух городов, расстояние между которыми 462 км навстречу друг другу выехали две машины. Одна ехала со скоростью 86 км/ч, а другая 68 км/ч. Какое расстояние будет между ними через 2 часа? A) 155 км B) 156 км C) 153 км D) 154 км E) 157 км |
7. Выполните вычитание неравенств (почленно): из  вычесть вычесть  A)
A)  B)
B)  C)
C)  D)
D)  E)
E) 
|
8. Решите систему неравенств  A) [3; +
A) [3; +  )
B) [– )
B) [–  ; + ; +  )
C) [– 3; 0) )
C) [– 3; 0)  [3; + [3; +  )
D) (3; + )
D) (3; +  )
E) [ )
E) [  ; 3] ; 3]
|
| 9. Последовательность задана формулой bn= n2 + 3. Найдите ее четвертый член. A) 11 B) 15 C) 19 D) 3n2 E) 7 |
| 10. Обратная пропорциональность – это функция, графиком которой является A) окружность B) прямая линия C) гипербола D) точка E) парабола |
11. Изобразив схематически график функции 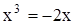 , выясни, сколько корней имеет уравнение
A) 2
B) 3
C) 4
D) нет корней
E) 1 , выясни, сколько корней имеет уравнение
A) 2
B) 3
C) 4
D) нет корней
E) 1
|
12. Какое из следующих неравенств не следует из неравенства a > b – c?
A) a – b + c  B) a – b – c > 0
C) b – c – a
B) a – b – c > 0
C) b – c – a  D) a + c > b
E) b < a + c
D) a + c > b
E) b < a + c
|
| 13. В пачке «Снежинка» 500 листов белой бумаги формата А4. За неделю в офисе расходуется 1300 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 5 недель? A) 10 B) 11 C) 13 D) 14 E) 12 |
14. Разложить многочлен  на множители:
A) на множители:
A)  B)
B)  C)
C)  D)
D)  E)
E) 
|
15. Корень уравнения  равен:
A) равен:
A) 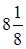 B)
B)  C) 10,5
D)
C) 10,5
D)  E)
E) 
|
16. Решите систему уравнений:  A) x = 6; y = – 5
B) x = 5; y = – 6
C) x = – 6; y = 5
D) x = – 6; y = – 5
E) x = 6; y = 5
A) x = 6; y = – 5
B) x = 5; y = – 6
C) x = – 6; y = 5
D) x = – 6; y = – 5
E) x = 6; y = 5
|
| 17. Пересечением промежутков [– 5; 8] и (– 8; 6) является промежуток: A) (– 8; 8] B) [– 5; 6] C) [– 5; 6) D) (– 5; 6) E) [– 5; 8] |
18. Найдите  ый член и разность арифметической прогрессии, если ый член и разность арифметической прогрессии, если  и и  A)
A)  B)
B) 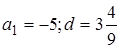 C)
C) 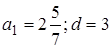 D)
D)  E)
E) 
|
19. Сократите дробь  .
A) .
A) 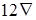 B)
B)  C)
C)  D)
D)  E)
E) 
|
| 20. Из-за непрекращающихся, длительное время, проливных дождей уровень воды в реке каждые сутки повышается на 20 см. В седьмой день наблюдений уровень воды достиг отметки 2,4 м. В первый день наблюдений уровень воды был на отметке. A) 1 м B) 1,2 м C) 1,8 м D) 1,6 м E) 1,4 м |
21. Решите уравнение:  A)
A)  B) 1
C) 4
D) 3
E)
B) 1
C) 4
D) 3
E) 
|
| 22. Сумма двух чисел равна 348. Если второе число на 6 больше, чем 80% первого,то первое число равно A) 180 B) 164 C) 190 D) 186 E) 172 |
23. При каких значениях n система уравнений  , имеет единственное решение.
A) , имеет единственное решение.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
|
24. Определите уравнение окружности, изображенной на рисунке.
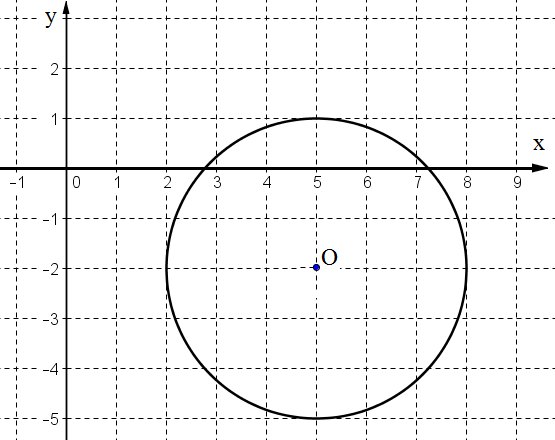 A)
A)  B)
B) 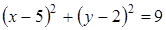 C)
C) 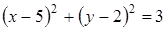 D)
D) 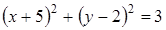 E)
E) 
|
25. По графикам функций, изображённым на рисунке, найдите истинное утверждение.
 A) f(1) < 0, g(1) > 0
B) f(–2) > g(–2)
C) g(6) + f(6) < 0
D) g(0)+f(2) < 0
E) g(1) < f(3)
A) f(1) < 0, g(1) > 0
B) f(–2) > g(–2)
C) g(6) + f(6) < 0
D) g(0)+f(2) < 0
E) g(1) < f(3)
|
Инструкция: «Вам предлагаются задания, в которых могут быть один или несколько правильных ответов. Выбранный ответ необходимо отметить на листе ответов путем полного закрашивания соответствующего кружка».
26. Значение выражения 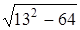 принадлежит промежутку:
A) принадлежит промежутку:
A) 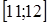 B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
|
27. Уравнения, которые имеют корни разных знаков
A)  B)
B)  C)
C)  D)
D) 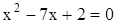 E)
E)  F)
F)  G)
G)  H)
H) 
|
28. Решите систему уравнений:  A) (10;3),(3;-4)
B) (2;-5),(5;-2)
C) (-10;1),(10;-1)
D) (2;-5),(7;0)
E) (3;-4),(4;-3)
F) (7;0)
G) (-2;9),(5;-2)
H) (5;-2),(2;-5)
A) (10;3),(3;-4)
B) (2;-5),(5;-2)
C) (-10;1),(10;-1)
D) (2;-5),(7;0)
E) (3;-4),(4;-3)
F) (7;0)
G) (-2;9),(5;-2)
H) (5;-2),(2;-5)
|
| 29. Двое рабочих, работая вместе, выполнили работу за 6 дней. За сколько дней может выполнить работу каждый рабочий, если одному из них для выполнения всей работы потребуется на 5 дней меньше, чем другому? A) 10 дней, 15 дней B) 9 дней, 14 дней C) 16 дней, 11 дней D) 14 дней, 9 дней E) 15 дней, 11 дней F) 17 дней, 12 дней G) 12 дней, 17 дней H) 15 дней, 10 дней |
30. Решите неравенство  A)
A) 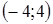 B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
|
31. Решите систему неравенств  A)
A)  B)
B) 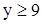 C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
|
32. Из следующих чисел решениями системы неравенств  являются
A) 2
B) 1
C) 5
D) -1
E) -2
F) 4
G) 0
H) 3 являются
A) 2
B) 1
C) 5
D) -1
E) -2
F) 4
G) 0
H) 3
|
33. Укажите координаты вершины параболы у=(х+1)2-4,2
A) (1;-4,2)
B) (-4,2;-1)
C) (-1;-4,2)
D) (4,2;-1)
E) (1;4,2)
F) (-1;  )
G) (-1;4,2)
H) (-1; )
G) (-1;4,2)
H) (-1;  ) )
|
| 34. Равенство, которое является пропорцией: A) 8,4:2,1=2,8+1,2 B) 6,6:2,2=0,3:0,1 C) 6,6:2,2=12−9 D) 6,6:2,2=6:2 E) 8,4:2,1=12:4 F) 8,4:2,1=4+1 G) 6,6:2,2=3:1 H) 8,4:2,1=2∙2 |
35. Корни уравнения  являются решением неравенства
A) х>1
B) х<4
C) х>4
D) х<7
E) х<3
F) х<6
G) х>3
H) х>2 являются решением неравенства
A) х>1
B) х<4
C) х>4
D) х<7
E) х<3
F) х<6
G) х>3
H) х>2
|
36. Решите систему уравнений: 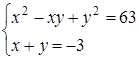 A) (3;-6),(-6;3)
B) (0;-3),(-4;1)
C) (0;-3)
D) (-3,0), (0;-3)
E) (-7;4)
F) (-5;2),(2,-5)
G) (-4;1),(0;-3)
H) (-6;3),(3;-6)
A) (3;-6),(-6;3)
B) (0;-3),(-4;1)
C) (0;-3)
D) (-3,0), (0;-3)
E) (-7;4)
F) (-5;2),(2,-5)
G) (-4;1),(0;-3)
H) (-6;3),(3;-6)
|
37. Решите неравенство  A)
A) 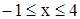 B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
|
38. Найдите первый член геометрической прогрессии, если  и и  A)
A)  B)
B)  C)
C)  D)
D) 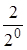 E)
E)  F)
F)  G)
G)  H)
H) 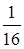
|
39. Упростите выражение  A)
A)  B)
B)  C)
C)  D) 3,5
E) 4,5
F)
D) 3,5
E) 4,5
F)  G)
G)  H)
H) 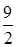
|
40. Решите уравнение  A)
A) 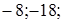 B)
B) 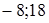 C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H)  ТЕСТ ПО ПРЕДМЕТУ АЛГЕБРА
ЗАВЕРШЁН
ТЕСТ ПО ПРЕДМЕТУ АЛГЕБРА
ЗАВЕРШЁН
|
АЛГЕБРА
Инструкция: «Вам предлагаются задания с одним правильным ответом из пяти предложенных. Выбранный ответ необходимо отметить на листе ответов путем полного закрашивания соответствующего кружка».
1. Вычислите:  A)
A) 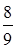 B) 0
C) 0,5
D) –1
E) 1
B) 0
C) 0,5
D) –1
E) 1
| ||||||||||||||
2. Упростите выражение и найдите его значение: 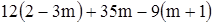 , если , если 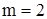 A) –2
B) –7
C) 3
D) 5
E) –5
A) –2
B) –7
C) 3
D) 5
E) –5
| ||||||||||||||
| 3. Решите уравнение: 0,12 – 2,5х = – 0,88 A) 0,5 B) 0,2 C) 0,3 D) 0,4 E) 0,6 | ||||||||||||||
4. Указать промежуток, содержащий больший корень квадратного уравнения  или корень этого уравнения, если он единственный:
A) или корень этого уравнения, если он единственный:
A)  B) (–3;– 1)
C)
B) (–3;– 1)
C) 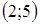 D)
D)  E)
E) 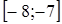
| ||||||||||||||
5. Решите систему уравнений: 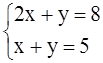 A) (2,5; 2,5)
B) (3; 2)
C) (2; 3)
D) (4; 1)
E) (1; 4)
A) (2,5; 2,5)
B) (3; 2)
C) (2; 3)
D) (4; 1)
E) (1; 4)
| ||||||||||||||
| 6. Сумма двух чисел в 7 раз больше их разности, а разность их квадратов равна 252. Найдите эти числа. A) 26;18 B) 42;18 C) 24;18 D) 56;18 E) 38;18 | ||||||||||||||
7. Указать промежуток, удовлетворяющий неравенству:  A)
A)  B)
B)  C)
C)  D)
D)  E)
E) 
| ||||||||||||||
8. Найдите наименьшее целое решение системы неравенств:  A) – 1
B) 1
C) 3
D) – 2
E) 2
A) – 1
B) 1
C) 3
D) – 2
E) 2
| ||||||||||||||
9. Найдите пятый член геометрической прогрессии, если ее первый член 9, второй член 3.
A)  B)
B)  C) 33
D) 39
E)
C) 33
D) 39
E) 
| ||||||||||||||
| 10. Найдите значение для функции: f(x) = 3– 14х – х2 f(– 2)=? A) 25 B) – 18 C) 27 D) 21 E) 24 | ||||||||||||||
11. Областью определения функции y =  является промежуток:
A) (– 5; + является промежуток:
A) (– 5; +  )
B) (5; + )
B) (5; +  )
C) (– )
C) (–  ; 5) ; 5)  (5; + (5; +  )
D) R
E) (– )
D) R
E) (–  ; – 5) ; – 5)
| ||||||||||||||
12. Запиши с помощью дроби, какая часть фигуры закрашена.
 A)
A)  B)
B)  C)
C) 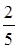 D)
D)  E)
E) 
| ||||||||||||||
| 13. Автомобиль проезжает 10 км за 8 минут. Сколько км он проедет за 2 часа без остановок, если продолжит поездку с этой же скоростью? A) 180 км B) 160 км C) 150 км D) 170 км E) 140 км | ||||||||||||||
14. Упростите выражение:  A) a3
B)
A) a3
B)  C)
C)  D)
D)  E)
E) 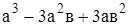
| ||||||||||||||
15. Решите уравнение:  A)
A)  B)
B)  C)
C)  D)
D)  E)
E) 
| ||||||||||||||
16. Решите систему уравнений:  A) (5; 1)
B) (– 3; 1), (– 1; 3)
C) (1; 3), (– 1; – 3)
D) (3; 1), (– 3; – 1)
E) (1; – 3), (3; – 1)
A) (5; 1)
B) (– 3; 1), (– 1; 3)
C) (1; 3), (– 1; – 3)
D) (3; 1), (– 3; – 1)
E) (1; – 3), (3; – 1)
| ||||||||||||||
17. Решите неравенство:  A) х >
A) х >  B) х < –
B) х < –  C) х > –
C) х > –  D) х < –
D) х < –  E) х <
E) х < 
| ||||||||||||||
| 18. В возрастающей геометрической прогрессии b1 =3, а сумма первых трех членов равна 21, тогда четвертый член прогрессии равен: A) 16 B) 26 C) 24 D) 14 E) 25 19. В таблице указано количество баллов, набранных учащимися на пробном тестировании. Определите средний балл и округлите его до сотых. | ||||||||||||||
A) 14,72 B) 14,82 C) 14,8 D) 14,7 E) 14,71 | ||||||||||||||
20. На диаграмме указаны средние цены (в тенге) на бакалейную продукцию.
 Определите стоимость следующего набора продуктов: 0,6 кг фасоли,
1,7 кг гречневой крупы, 3,1 кг сахара.
A) 884,4 тенге
B) 894,4 тенге
C) 884,3 тенге
D) 885,4 тенге
E) 885,3 тенге
Определите стоимость следующего набора продуктов: 0,6 кг фасоли,
1,7 кг гречневой крупы, 3,1 кг сахара.
A) 884,4 тенге
B) 894,4 тенге
C) 884,3 тенге
D) 885,4 тенге
E) 885,3 тенге
| ||||||||||||||
21. Упростите выражение:  A)
A)  B)
B)  C)
C)  D)
D) 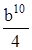 E)
E) 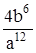
| ||||||||||||||
| 22. В зале клуба столько рядов, сколько мест в каждом ряду. Если увеличить в 2 раза число рядов и уменьшить на 10 количество мест в ряду, то число мест в зале увеличится на 300. Рядов в зале: A) 25 B) 10 C) 20 D) 100 E) 30 | ||||||||||||||
23. Найдите область определения функции: 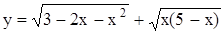 A) [0;3]
B) [1;5]
C) [0;5]
D) [–3;0]
E) [0;1]
A) [0;3]
B) [1;5]
C) [0;5]
D) [–3;0]
E) [0;1]
| ||||||||||||||
24. Если  , то A + B + C равно
A) 8
B) 6
C) 4
D) 7
E) 5 , то A + B + C равно
A) 8
B) 6
C) 4
D) 7
E) 5
| ||||||||||||||
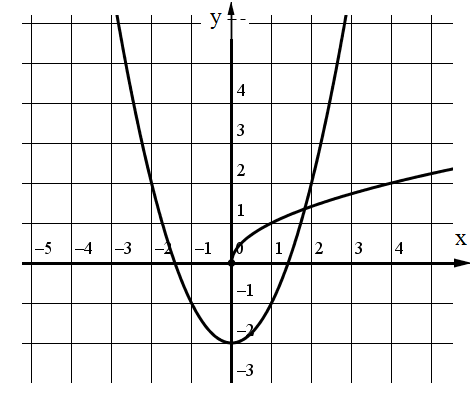
25. На рисунке изображено графическое решение уравнения
 A)
A) 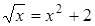 B)
B)  C)
C)  D)
D)  E)
E) 
| ||||||||||||||
Инструкция: «Вам предлагаются задания, в которых могут быть один или несколько правильных ответов. Выбранный ответ необходимо отметить на листе ответов путем полного закрашивания соответствующего кружка».
26. Упростите выражение:    A)
A)  B)
B)  C)
C)  D)
D) 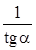 E)
E)  F)
F)  G)
G)  H)
H)  
| ||||||||||||||
| 27. Из предложенных уравнений выберите, которые не имеют решения A) 12х – 21= 5х + 7(х – 3) B) 0х = 0,2 C) 3х − 1,5 = х + 2(х − 0,5) D) 5х – 100 = 8(10 + 5х) E) 0,2х = 0 F) 4х − 8,5 = 2(2х − 0,5) − 7,5 G) 9 + 2х = 2х + 9 H) 3(х − 2) = 5 + 3х | ||||||||||||||
28. Найдите  где где  решение систему уравнений: решение систему уравнений:  A)
A)  B) 10
C) 12
D) 0
E) 13
F)
B) 10
C) 12
D) 0
E) 13
F)  G) 14
H)
G) 14
H) 
| ||||||||||||||
| 29. Сумма двух смежных сторон прямоугольника равна 27 см, а площадь −180 см2. Тогда стороны прямоугольника A) 15 см, 12 см B) 12 см, 15 см C) 10 см, 17 см D) 10 см, 18 см E) 18 см, 10 см F) 1,2 дм, 1,5 дм G) 12 см, 16 см H) 17 см, 10 см | ||||||||||||||
30. Решите неравенство:  A)
A)  B)
B)  C)
C)  D)
D)  E)
E)  F)
F) 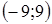 G)
G)  H)
H) 
| ||||||||||||||
31. Найдите решение системы неравенств: 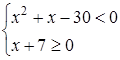 A) [− 6;5]
B) x≥7
C) x≥
A) [− 6;5]
B) x≥7
C) x≥  D)
D)  E)
E)  F)
F)  ; ;  G)
G)  H) (− 6;5)
H) (− 6;5)
| ||||||||||||||
32. Одинаковое множество решений имеют следующие неравенства:
A) 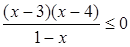 B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
| ||||||||||||||
33. График функции  проходит через точку…
A) проходит через точку…
A)  B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
| ||||||||||||||
34. Укажите числа, обратные значению числового выражения  A)
A) 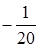 B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 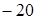
| ||||||||||||||
35. Решите уравнение: (2х + 5,2): (− 3) = 4,1: (− 1,5)
A)  B) − 2
C) − 1,5
D) 2
E)
B) − 2
C) − 1,5
D) 2
E)  F) 1,5
G)
F) 1,5
G)  H)
H) 
| ||||||||||||||
36. Сумма решений системы уравнений принадлежит промежутку  A)
A) 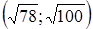 B)
B) 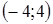 C)
C)  D)
D)  E)
E)  F)
F)  G)
G) 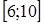 H)
H) 
| ||||||||||||||
| 37. Найдите целые решения неравенства: х(x − 2,5)(x + 1)2 ≤0 A) 0 B) − 1; 0 C) − 1; 0; 1 D) − 1; 0; 2 E) − 1; 1; 0; 2 F) − 1; 0; 1; 2 G) ±1; 0;2 H) 1; 2 | ||||||||||||||
38. Найдите первый член геометрической прогрессии, если
 и и  A)
A)  B)
B)  C)
C)  D)
D)  E)
E)  F)
F) 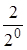 G)
G) 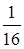 H)
H) 
| ||||||||||||||
39. Из следующих утверждений верны
A)  B)
B)  C)
C)  D)
D)  E)
E)  F)
F)  G)
G)  H)
H) 
| ||||||||||||||
40. Корень уравнения  равен:
A) равен:
A)  B)
B)  C)
C)  D)
D)  E) 8
F)
E) 8
F)  G)
G)  H)
H)  ТЕСТ ПО ПРЕДМЕТУ АЛГЕБРА
ЗАВЕРШЁН
ТЕСТ ПО ПРЕДМЕТУ АЛГЕБРА
ЗАВЕРШЁН
|
Тесты аттестация Алгебра
1. Вычислите: 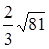 A) 3
B) 6
C) 12
D) 18
E) 9
A) 3
B) 6
C) 12
D) 18
E) 9
|
2. Вычислите: 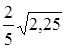 A) 6
B) 0,6
C) 4
D) 0,3
E) 3
A) 6
B) 0,6
C) 4
D) 0,3
E) 3
|
3. Вынесите множитель из-под знака корня  A) 5
A) 5  B) 10
B) 10  C) 2
C) 2  D) 5
D) 5  E) 25
E) 25
|
4. Вычислите:  A) 11,5
B) 10,5
C) 1,6
D) 6
E) 0,6
A) 11,5
B) 10,5
C) 1,6
D) 6
E) 0,6
|
5. Упростите выражение  A)
A)  B)
B) 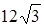 C)
C)  D) – 2
E)
D) – 2
E) 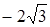
|
6. Вынесите множитель из-под знака корня  A) 2
A) 2  B) 3
B) 3  C) 4
C) 4  D) 6
E) 3
D) 6
E) 3 
|
7. Решите уравнение  A) – 1 и 1
B)
A) – 1 и 1
B)  C) – 2 и 2
D)
C) – 2 и 2
D)  и и  E)
E) 
|
8. Решите уравнение  A) 4
B) 3
C) – 4
D) 4 и 3
E) 8
A) 4
B) 3
C) – 4
D) 4 и 3
E) 8
|
9. Решите уравнение  A) – 3 и 0
B) 3
C) 0 и 3
D) 0
E) – 3
A) – 3 и 0
B) 3
C) 0 и 3
D) 0
E) – 3
|
| 10. Ширина прямоугольника на 2 см меньше его длины. Найдите ширину и длину прямоугольника, если его площадь равна 120 см2. A) 6 см и 20 см B) 3 см и 40 см C) 5 см и 24 см D) 10 см и 12 см E) 4 см и 30 см |
11. Решите уравнение  A)
A)  ; 2
B) ; 2
B)  ; 2
C) 2
D) ; 2
C) 2
D)  E) –2;
E) –2; 
|
| 12. Найдите меньшее из двух чисел, сумма которых равна 22, а сумма их квадратов равна 250 A) 7 B) 8 C) 12 D) 11 E) 9 |
13. Найдите второй корень уравнения  , если первый корень
равен – 4
A) –3
B) 5
C) –8
D) 3
E) 8 , если первый корень
равен – 4
A) –3
B) 5
C) –8
D) 3
E) 8
|
14. Разложите на множители квадратный трехчлен  A)
A) 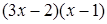 B)
B)  C)
C)  D)
D)  E)
E) 
|
15. Укажите значения аргумента, при которых функция  обращается в нуль.
A) 3 и 5
B) 1 и 2
C) –5 и 3
D) –5 и –3
E) –5 и 2 обращается в нуль.
A) 3 и 5
B) 1 и 2
C) –5 и 3
D) –5 и –3
E) –5 и 2
|
16. Укажите квадратный трехчлен, который можно разложить на множители
A)  B)
B)  C)
C)  D)
D) 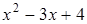 E)
E) 
|
17. Укажите значение переменной, при которых выражение  имеет смысл
A) имеет смысл
A)  B)
B)  C)
C)  D)
D)  E)
E) 
|
18. Решите неравенство  A)
A)  B)
B)  C)
C)  D)
D) 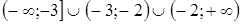 E)
E) 
|
19. Найдите наименьшее целое решение неравенства:  A) – 2
B) – 3
C) 8
D) – 7
E) – 8
A) – 2
B) – 3
C) 8
D) – 7
E) – 8
|
20. Игральный кубик бросили 48 раз. В таблице указаны числа выпадений каждой из цифр: 1, 2, 3, 4, 5, 6.
Найдите вероятность появления цифры 3. A) B) C) D) E)
|
Алгебра
1. Освободите от иррациональности знаменатель дроби 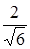 A)
A)  B)
B)  C)
C)  D)
D)  E)
E) 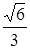
|
2. Вынесите множитель из-под знака корня  A) 3
A) 3  B) 2
B) 2  C) 4
C) 4  D) 3
D) 3  E) 16
E) 16
|
3. Внесите множитель под знак корня  A)
A)  B)
B)  C)
C) 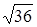 D)
D)  E)
E) 
|
4. Составьте квадратное уравнение по его корням 2 и 3
A)  B)
B) 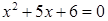 C)
C)  D)
D)  E)
E) 
|
5. Решите уравнение:  A) – 4
B) 4
C) 4 и 3
D) 3
E) 8
A) – 4
B) 4
C) 4 и 3
D) 3
E) 8
|
6. Решите уравнение:  A) 0
B) 4 и 0
C) – 2 и 2
D) – 4 и 0
E) – 4
A) 0
B) 4 и 0
C) – 2 и 2
D) – 4 и 0
E) – 4
|
7. Составьте квадратное уравнение по его корням 1 и 2
A) 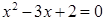 B)
B) 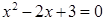 C)
C)  D)
D)  E)
E) 
|
8. На каком рисунке изображен график функции  A)
A)
 B)
B)
 C)
C)
 D)
D)
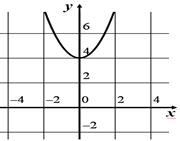 E)
E)
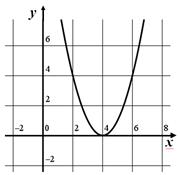
|
9. Укажите число, которое является решением неравенства  .
A) 5
B) 6
C) – 4
D) – 3
E) 0 .
A) 5
B) 6
C) – 4
D) – 3
E) 0
| ||||||||||||||||||||
10. Данные регистрации числа пассажиров, ожидающих на остановке автобус определенного маршрута, занесены в таблицу
Укажите время, в которое наблюдается наибольшее количество пассажиров. A) 13.00 B) 19.00 C) 11.00 D) 21.00 E) 17.00
| ||||||||||||||||||||
| 11. Катер за один час проплыл 15 км по течению реки и 4 км в стоячей воде. Скорость течения реки в 4 раза меньше скорости катера в стоячей воде. Найдите собственную скорость катера A) 16 км/ч B) 14 км/ч C) 10 км/ч D) 20 км/ч E) 12 км/ч | ||||||||||||||||||||
12. Решите систему неравенств
  ; ;
 .
A) .
A)  B)
B)  C)
C)  D)
D)  E)
E) 
| ||||||||||||||||||||
13. Решите систему уравнений
  , ,
 .
A) (–7; 9); (4; –2)
B) (–7; 9); (–2; 4)
C) (–7; 9)
D) (4; –2)
E) (9; –7); (–2; 4) .
A) (–7; 9); (4; –2)
B) (–7; 9); (–2; 4)
C) (–7; 9)
D) (4; –2)
E) (9; –7); (–2; 4)
| ||||||||||||||||||||
14. Укажите уравнение окружности, изображенной на рисунке
 A)
A) 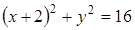 B)
B)  C)
C)  D)
D)  E)
E) 
| ||||||||||||||||||||
| 15. Найдите площадь прямоугольника, длина которого в 4 раза больше, чем ширина, а величина площади равна периметру. A) 25 кв.ед. B) 20 кв.ед. C) 15 кв.ед. D) 35 кв.ед. E) 30 кв.ед. | ||||||||||||||||||||
| 16. В арифметической прогрессии а1 = 10, S11 = 330. Найдите а11. A) 60 B) 50 C) 70 D) 40 E) 80 | ||||||||||||||||||||
| 17. Найти шестой член последовательности { ап }, если а1 = 1, а п+1 = ап + 1 A) 6 B) 8 C) 10 D) 5 E) 11 | ||||||||||||||||||||
18. Определите, при каких значениях a последовательность, заданная формулой общего члена  , является убывающей.
A) , является убывающей.
A)  B)
B)  C)
C) 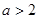 D)
D)  E)
E) 
| ||||||||||||||||||||
| 19. Найдите четыре числа, образующие геометрическую прогрессию, если их сумма равна 160 и последнее число в 27 раз больше первого A) 4; 12; 36; 108 B) – 4; –12; –36; –108 C) 3; 9; 27; 81 D) – 3; –9; –27; –81 E) 5; 15; 45; 135 | ||||||||||||||||||||
20. Найдите все значения х, при которых значения выражений 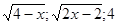 являются последовательными членами геометрической прогрессии.
A) 5
B) 1
C) 2
D) 3
E) 4 являются последовательными членами геометрической прогрессии.
A) 5
B) 1
C) 2
D) 3
E) 4
|
Тест по предмету Алгебра завершен










