Плотностью распределения вероятностей f (x) непрерывной случайной величины Х называется первая производная от функции распределения, т.е.
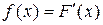(5.6)
Из формулы (5.6) следует, что функция распределения, в свою очередь, является первообразной от функции плотности. Именно поэтому функцию плотности иногда называют дифференциальной функцией распределения, а, как уже было отмечено, функцию распределения – интегральной.
Функция плотности является в некотором смысле более "удобной" функцией для характеристики распределения непрерывной случайной величины. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки вещественной оси. Эта задача более успешно может быть решена с помощью функции плотности.
К понятию функции плотности можно придти через механическую интерпретацию. Для этого вначале вспомним дискретную случайную величину и ее ряд распределения:
| Х | х 1 | х 2 | … | х n |
| Р | р 1 | р 2 | … | р n |
Так как р 1+ р 2+…+ р n=1, то можно, например, предположить, что некая масса в один килограмм распределена между точками х 1, х 2, …, х n в количествах, равных соответствующим вероятностям р 1, р 2, …, р n. Пусть теперь общая масса не сосредоточена в отдельных точках х 1, х 2, …, х n, а как-то непрерывно "размазана" по вещественной оси, в общем случае, с неравномерной плотностью.
Рассмотрим некоторый участок [ x, x +Δ х) вещественной оси. Вероятность Р (х ≤ Х < x +Δ х) попадания случайной величины на данный участок может интерпретироваться как количество общей массы приходящейся на этот участок. Средняя плотность – это отношение рассмотренной массы к длине участка, т.е. 
.
Так как вероятность попадания значений случайной величины на некоторый участок равна приращению функции распределения на этом участке, то средняя плотность будет равна: 
.
Для определения плотности в какой-то точке х, необходимо в правой части последнего равенства перейти к пределу при Δ х →0, т.е. когда длина рассматриваемого участка стремиться к нулю, получим
.
Последнее равенство вытекает из определения производной. Эта производная существует, так как в определении непрерывной случайной величины было введено условие дифференцируемости функции распределения.
Еще раз подчеркнем, что функция плотности существует только для непрерывных случайных величин и является одной из, наиболее часто применяемых на практике, форм закона распределения вероятностей этих величин.
Если непрерывная случайная величина Х имеет функцию плотности (или просто плотность) f (х), то говорят, что эта величина имеет распределение (или просто распределена) с плотностью f (х).
График функции плотности называется кривой распределения.
Из формулы (5.6) ясно, что, в свою очередь, функция распределения является первообразной для функции плотности. Следовательно, эти функции связывает формула Ньютона-Лейбница нахождения определенного интеграла из математического анализа: 
.
Так как правая часть этой формулы по свойству функции распределения равна вероятности попадания случайной величины на интервал (a, b), то имеет место следующая формула: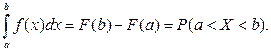 
Таким образом была доказана следующая теорема.
Теорема 5.1. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), вычисляется по формуле:
(5.7)
Формула (5.7) имеет простой геометрический смысл: вероятность попадания случайной величины на интервал (a, b) численно равна площади криволинейной трапеции, ограниченной графиком функции f (x), осью Ох и прямыми х = а и х = b.
 |
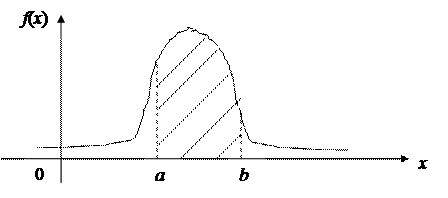Рис.5.7.
Пример 5.4. По заданной функции распределения
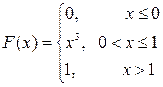
найти функцию плотности распределения, построить графики обеих функций и найти вероятность, того, что значение случайной величины Х попадет в интервал (0,5; 0,75).
Решение. Найдем функцию плотности, используя формулу (5.6), получим
.
Построим графики обеих функций:
 |
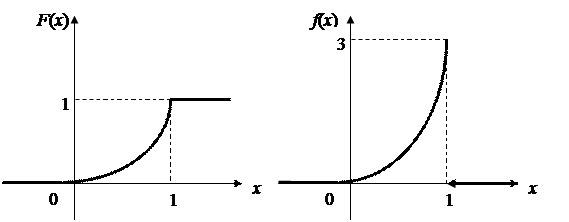Рис.5.8.
Найдем требуемую вероятность, используя формулу (5.7), получим
Очевидно, что эта же вероятность могла бы быть найдена и с помощью функции распределения:
■
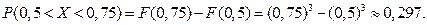Из формулы (5.7) сразу следует формула для нахождения функции распределения, а именно, положив а = −∞, а b = х, получим
(5.8)
Пример 5.5. По заданной функции плотности найти функцию распределения
.
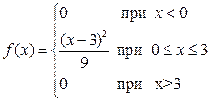Решение. Воспользуемся формулой (5.8), получим:
если х <0, то f (x)=0 и, следовательно, для этих х
;
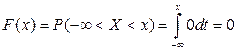если 0≤ х ≤3, то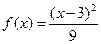 
и, следовательно, для этих х
;
если х >3, то f (x)=0 и, следовательно, для этих х
.
Таким образом, функция F (x) имеет вид:
. ■
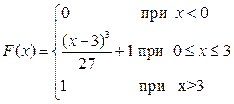