«акон распределени€ веро€тностей непрерывной случайной величины называетс€ показательным или экспоненциальным, если функци€ плотности этой величины имеет вид:
 , (7.5)
, (7.5)
где λ Ц посто€нна€ положительна€ величина, называема€ параметром данного распределени€.
√рафик показательного распределени€ имеет вид (рис.7.3):
 |
–ис.7.3.
ќдним из преимуществ показательного распределени€ €вл€етс€ то, что оно зависит только от одного параметра λ.
Ќайдем функцию распределени€ показательного закона. »спользуем формулу (5.8) и, прежде всего, найдем выражение F (x) дл€ положительных х:
 .
.
ѕри х ≤ 0 функци€ F (x) = 0. “аким образом,
 .
.
√рафик функции распределени€ имеет вид (рис.7.4):
 |
–ис.7.4.
Ќайдем основные числовые характеристики случайной величины, распределенной по показательному закону.
ѕо формуле (6.2) находим математическое ожидание:
 .
.
ѕри нахождении интеграла использовалась формула интегрировани€ по част€м, и учитывалось, что при х →+∞ функци€  стремитьс€ к нулю быстрее, чем возрастает люба€ степень х.
стремитьс€ к нулю быстрее, чем возрастает люба€ степень х.
“аким образом, математическое ожидание случайной величины, распределенной по показательному закону, обратно его параметру λ.
ѕо формуле (6.6) найдем дисперсию, получим
 .
.
ƒл€ нахождени€ дисперсии формула интегрировани€ по част€м примен€лась дважды.
—реднеквадратическое отклонение равно  .
.
»так, дл€ показательного распределени€ среднеквадратическое отклонение совпадает с математическим ожиданием.
„тобы найти асимметрию показательного распределени€ найдем его третий центральный момент, при этом дл€ нахождени€ интеграла формулу интегрировани€ по част€м приходитс€ применить трижды.
 .
.
и, следовательно, коэффициент асимметрии  . ак и следовало ожидать, асимметри€ показательного распределени€ положительна.
. ак и следовало ожидать, асимметри€ показательного распределени€ положительна.
ƒл€ нахождени€ эксцесса поступаем аналогично, но находим четвертый центральный момент, после преобразований, получим ≈k =6.
Ќайдем веро€тность попадани€ в интервал (а, b) непрерывной случайной величины ’, распределенной по показательному закону. ƒл€ этого будем использовать функцию распределени€ и формулу (5.3):
 .
.
«начени€ функции  наход€т по таблице.
наход€т по таблице.
ѕоказательное распределение имеют, например, величины срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий. ѕоказательное распределение играет большую роль в теории марковских случайных процессов, теории массового обслуживани€ и теории надежности.
Ќормальный закон распределени€ непрерывной
—лучайной величины
Ќормальный закон распределени€ или закон √аусса играет огромную роль в теории веро€тностей и ее приложени€х и занимает исключительно важное, особое положение. Ќормальный закон распределени€ €вл€етс€ предельным законом при определенных услови€х дл€ некоторых других законов распределени€.
«акон распределени€ веро€тностей непрерывной случайной величины называетс€ нормальным или законом √аусса, если функци€ плотности этой величины имеет вид:
|
|
|
 , (7.6)
, (7.6)
где т и σ Ц некоторые посто€нные, называемые параметрами нормального распределени€.
Ќайдем функцию распределени€ нормального закона. Ќа основании формулы (5.8) получим
 .
.
Ќайдем числовые характеристики нормально распределенной случайной величины. ѕо определению
 .
.
¬ведем новую переменную по формуле 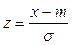 . “огда
. “огда 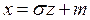 , а
, а  , причем, очевидно, что пределы интегрировани€ остаютс€ теми же. »так, получаем
, причем, очевидно, что пределы интегрировани€ остаютс€ теми же. »так, получаем
 .
.
ѕервый из интегралов в правой части полученного равенства равен нулю как интеграл от нечетной функции в симметричных пределах, а второй интеграл Ц это интеграл ѕуассона, который равен  . —ледовательно,
. —ледовательно,
 .
.
“аким образом, параметр т нормального распределени€ равен математическому ожиданию соответствующей случайной величины, т.е. т = ћ (’).
”чтем полученный результат при нахождении дисперсии:

¬ведем новую переменную по формуле  . ¬ результате чего получим
. ¬ результате чего получим
 .
.
ƒалее, после применени€ формулы интегрировани€ по част€м, получим
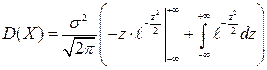 .
.
ѕервое слагаемое в скобках равно нулю, так как  по правилу Ћопитал€, а второе слагаемое, уже известный интеграл ѕуассона, равно
по правилу Ћопитал€, а второе слагаемое, уже известный интеграл ѕуассона, равно  .
.
ќтсюда,  .
.
»так, дисперси€ нормально распределенной случайной величины ’ равна квадрату второго параметра, т.е.  , а, следовательно, сам второй параметр определ€ет среднеквадратическое отклонение. ¬ дальнейшем, дл€ нормально распределенной случайной величины будем использовать следующие обозначени€:
, а, следовательно, сам второй параметр определ€ет среднеквадратическое отклонение. ¬ дальнейшем, дл€ нормально распределенной случайной величины будем использовать следующие обозначени€:  и
и  .
.
ѕараметры нормального распределени€ имеют простую геометрическую интерпретацию. ƒл€ того чтобы это пон€ть исследуем функцию плотности и построим ее график. »сследование будем проводить по общей схемы из классического математического анализа.
»так, исследуетс€ функци€  .
.
1. ќбластью определени€ функции f (x) €вл€етс€ вс€ вещественна€ пр€ма€.
2. ‘ункци€ f (x) может принимать только положительные значени€, так как показательна€ функци€ не может принимать отрицательные значени€, а среднеквадратическое отклонение и арифметический корень также отрицательными быть не могут.
3. ќсь абсцисс €вл€етс€ горизонтальной асимптотой, так как
 .
.
4. ‘ункци€ f (x) в точке х = т имеет экстремум, равный
 .
.
ƒл€ доказательства возьмем первую производную и приравн€ем ее к нулю, получим
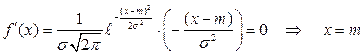 .
.
ѕри переходе через точку х = т производна€ мен€ет знак с плюса на минус. —ледовательно, в точке х = т функци€ f (x) имеет максимум. роме этого, очевидно, что на промежутке  функци€ f (x) возрастает, а на промежутке
функци€ f (x) возрастает, а на промежутке  функци€ f (x) убывает.
функци€ f (x) убывает.
5. √рафик функции f (x) симметричен относительно пр€мой х = т.
6. √рафик функции f (x) в точках  имеет перегиб.
имеет перегиб.
ƒл€ доказательства возьмем вторую производную и приравн€ем ее к нулю, получим
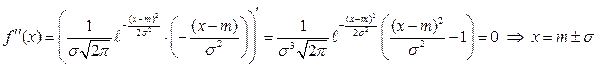 .
.
ѕри переходе через эти точки втора€ производна€ мен€ет знак, следовательно, 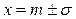 €вл€ютс€ точками перегиба.
€вл€ютс€ точками перегиба.
Ќа основании полученного исследовани€ строим график функции плотности нормального распределени€ f (x).
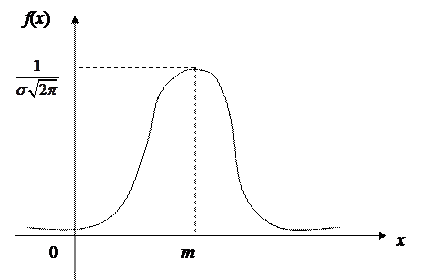 рива€ нормального распределени€ имеет симметричный холмообразный вид:
рива€ нормального распределени€ имеет симметричный холмообразный вид:
–ис.7.5.
¬ы€сним, как вли€ют параметры нормального распределени€ на график функции плотности.
ѕри изменении т крива€ f (x), не измен€€ своей формы, будет смещатьс€ вдоль оси абсцисс влево или вправо, в зависимости от того уменьшатьс€ или увеличиватьс€ будет число т: т 1 < т < т 2

–ис.7.6.
ѕри изменении σ будет мен€тьс€ масштаб кривой по обеим ос€м. ѕри этом график функции будет либо выт€гиватьс€ вверх (при уменьшении σ), либо крива€ будет становитьс€ более плоской, раст€гива€сь вдоль оси абсцисс (при увеличении σ):
|
|
|
 |
–ис.7.7.
»спользу€ определение центральных моментов дл€ нормального распределени€ и метод замены переменной при нахождении интегралов, можно получить следующее рекуррентное соотношение:
 .
.
ƒанна€ формула позвол€ет выражать центральные моменты более высоких пор€дков через центральные моменты более низких пор€дков. “ак, например, очевидно, что все центральные моменты нечетного пор€дка равны нулю, так как μ 1=0. “аким образом, асимметри€, равна€ центральному моменту, равна нулю, следовательно, распределение симметрично относительно своего математического ожидани€, что и было использовано при построении графика функции плотности. ¬ыше было найдено значение дисперсии D (X)= σ 2. “ак как дисперси€ Ц это второй центральный момент, то μ 2= σ 2. »спользу€ рекуррентную формулу, найдем центральный момент четвертого пор€дка: μ 4=3 σ 2 μ 2=3 σ 4, а затем эксцесс:  .
.
¬ шестой главе было рассмотрено пон€тие стандартной случайной величины и доказана теорема о том, что математическое ожидание стандартной величины равно 0, а дисперси€ Ц 1. ƒл€ нормального распределени€ тоже можно указать стандартную случайную величину, т.е. величину, параметры которой равны т =0 и σ =1. ‘ункци€ плотности стандартной нормально распределенной случайной величины равна
 (7.7)
(7.7)
»так, формула (7.7) определ€ет функцию плотности распределени€ случайной величины  , где ’ Ц случайна€ величина, распределенна€ по нормальному закону с параметрами т и σ. «начени€ функции
, где ’ Ц случайна€ величина, распределенна€ по нормальному закону с параметрами т и σ. «начени€ функции  приведены в приложении 1.
приведены в приложении 1.
¬ычислим веро€тность попадани€ нормально распределенной случайной величины на некоторый интервал (а, b). Ќо прежде напомним определение некоторой специальной функции.
‘ункцией Ћапласа или интегралом веро€тностей ‘(х) называетс€ следующий определенный интеграл
 (7.8)
(7.8)
»нтеграл в формуле (7.8) не выражаетс€ через элементарные функции, но дл€ нахождени€ значений функции ‘(х) существует таблица (приложение 2).
‘ункци€ Ћапласа обладает следующими свойствами:
1. ‘(0)=0;
2. ‘(Ц х)=Ц‘(х) Ц функци€ нечетна€;
3. ‘(Ц∞)=Ц0,5; ‘(+∞)=0,5.
Ќеобходимо отметить, что в некоторых учебниках по теории веро€тностей за функцию Ћапласа принимают не функцию (7.8), а другую, отличающуюс€ от нее посто€нным множителем.
ѕерейдем теперь к нахождению веро€тности попадани€ случайной величины на интервал. »спользуем формулу (5.7) и (7.6), получим
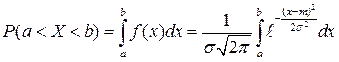 .
.
—делав в последнем интеграле замену переменной  и применив формулу (7.8), получим
и применив формулу (7.8), получим
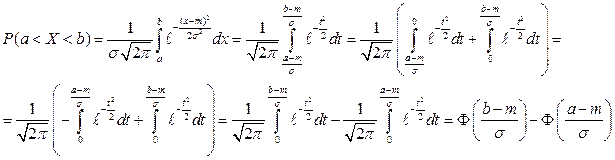
»так, веро€тность попадани€ нормально распределенной случайной величины ’ на интервал (а; b) может быть вычислена по формуле
 (7.9)
(7.9)
— помощью формулы (7.9) можно функцию распределени€ F (x) выразить через функцию Ћапласа, а именно
 .
.
ѕример 7.5. «авод изготавливает шарики дл€ подшипников, номинальный диаметр которых равен 10 мм, а фактический диаметр случаен и распределен по нормальному закону с т =10 мм и σ =0,4 мм. ѕри контроле бракуютс€ все шарики, не проход€щие через круглое отверстие с диаметром d 1=10,7 мм и все, проход€щие через круглое отверстие с диаметром d 2=9,3 мм. Ќайти процент брака.
–ешение. ѕусть ’ Ц фактический диаметр. “ак как по условию задачи ’ распределена по нормальному закону, то можно применить формулу (7.9) и найти веро€тность того, шарик не попадет в брак, т.е. диаметр окажетс€ в допустимых пределах
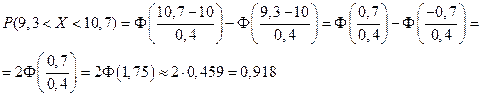
ѕри нахождении значени€ функции ‘(1,75) использовалась таблица значений функции Ћапласа (приложение 2). ќтсюда веро€тность того, что шарик окажетс€ бракованным, равна 1− 0,918 = 0,082. —ледовательно, 8,2% шариков будут забракованы. ■
ѕример 7.6. ѕусть случайна€ величина ’ распределена по нормальному закону с параметрами т =20 и σ =10. Ќайти веро€тность того, что отклонение значений этой случайной величины от своего математического ожидани€ по абсолютной величине будет меньше трех.
|
|
|
–ешение. ѕо условию задачи необходимо найти следующую веро€тность
 .
.
ѕримен€€ формулу (7.9), получим
 .■
.■
–ешение примера 7.6 дает следующий частный случай формулы (7.9).
¬еро€тность попадани€ нормально распределенной случайной величины с параметрами т и σ на участок длиной 2 h, симметричный относительно центра рассеивани€ вычисл€етс€ по формуле
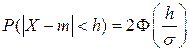 (7.10)
(7.10)
ѕример 7.7. —лучайна€ величина ’ распределена нормально с параметрами т и σ. Ќайти веро€тность того, что случайна€ величина ’ отклонитс€ от своего математического ожидани€ не больше, чем 3 σ.
–ешение. ѕо условию задачи, нужно найти веро€тность  ѕрименим формулу (7.10), получим
ѕрименим формулу (7.10), получим
 .■
.■
¬еро€тность, полученна€ в решении примера 7.7, достаточно велика. роме этого, она не зависит от величины математического ожидани€. Ќа основе этого результата можно предположить, что почти все значени€ случайной величины не отступают от математического ожидани€ на величину большую, чем 3 σ. »наче говор€, веро€тность того, что то или иное значение величины ’ не попадает в интервал с границами т ±3 σ равна 0,0027, т.е. близка к нулю. Ёто означает, что лишь в 0,27% случаев такое может произойти. “акие событи€ практически можно считать невозможными. ѕо сути, здесь было выведено одно из очень важных правил, относ€щихс€ к нормально распределенным случайным величинам, так называемое "правило трех сигм".
ѕравило трех сигм. ѕусть случайна€ величина ’ распределена по нормальному закону. “огда отклонение этой величины от своего математического ожидани€ по абсолютной величине практически не превышает утроенного среднеквадратического отклонени€.
ѕо этому правилу считают, что возможные значени€ нормально распределенной случайной величины практически не выход€т за пределы интервала [ m Ц 3 σ, m + 3 σ ]. ѕоэтому функцию плотности, в основном, и стро€т на этом интервале. роме этого, "правило трех сигм" может быть применено и дл€ установлени€ закона распределени€ некоторой случайной величины. “ак, например, если закон распределени€ случайной величины ’ неизвестен, само правило дл€ этой величины выполн€етс€, то есть основани€ предположить, что случайна€ величина ’ распределена по нормальному закону.
ќсоба€ роль, которую играет нормальный закон распределени€ в теории веро€тностей, св€зана с одним его замечательным свойством. ќказываетс€, что сумма достаточно большого числа независимых случайных величин, подчин€ющихс€ каким угодно законам распределени€, приближенно описываетс€ нормальным законом распределени€, причем тем точнее, чем больше число случайных величин суммируетс€. Ќапример, при массовом изготовлении гаек разброс значений их диаметра св€зан со случайными отклонени€ми характеристик материала, колебани€ми температуры, вибраци€ми станка, изменени€ми напр€жени€ в электросети, стачиванием инструмента и т.д. ¬се эти случайные факторы действуют примерно в одинаковой мере и независимо друг от друга. ќни суммируютс€, и в результате фактический диаметр гайки оказываетс€ непрерывной случайной величиной, описываемой нормальным законом распределени€. ћатематическое ожидание этой величины есть, очевидно, эталонное значение диаметра гайки, а дисперси€ характеризует степень разброса фактических значений диаметра около эталонного значени€.
јналогично рассужда€, можно придти к выводу, что очень многие ошибки измерени€ также имеют нормальный закон распределени€. ак уже отмечалось, нормальное распределение иногда называют распределением √аусса. ¬ работах √аусса это распределение и рассматривалось в св€зи с исследовани€ми по теории ошибок.
|
|
|
—амо пон€тие нормального распределени€ впервые по€вилось в работе ћуавра как предельна€ форма биномиального распределени€.
¬ заключение, рассмотрим еще одну задачу.
ѕример 7.8. —читаетс€, что отклонение длины изготавливаемых изделий от стандарта €вл€етс€ случайной величиной, распределенной по нормальному закону. ≈сли стандартна€ длина равна т =40 см и σ =0,4 см, то какую точность длины издели€ можно гарантировать с веро€тностью 0,8?
–ешение. ѕусть точность равна ε. “огда по условию задачи должно выполн€тьс€ неравенство 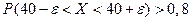 . Ќайдем значение ε, при котором достигаетс€ равенство, получим
. Ќайдем значение ε, при котором достигаетс€ равенство, получим
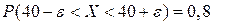



 . ■
. ■






