Порядок построения аппроксимирующей функции с использованием приложения Excel рассмотрим на примере построения линейной регрессии y=P1(x) = a+bx.
Будем находить параметры a, b, которые, согласно МНК, должны минимизировать сумму квадратов отклонений
. При этомминимизацию суммы будем реализовывать с помощью надстройки Excel «Поиск решения».
1. Оформим таблицу, как показано на рис.3.3. В ячейки А9:В15 введем результаты эксперимента (результаты эксперимента взять в приложении 3 в соответствии с вариантом). Эти данные являются исходными.
2. Подготовим ячейки В3:С3, в которых будут получены коэффициенты уравнения регрессии а, в. Для контроля проводимых ниже расчетов примите их равными единице, т.е. В3 =1, С3 =1. С «точки зрения» надстройки это изменяемые ячейки, а принятые значения а=1, в=1 можно считать начальным приближением.
3. В столбце С (Прямая) вычислите значения УР в экспериментальных точках:
· C9 = $B$3+$C$3*A9
· 
Скопируйте формулу вниз до конца таблицы
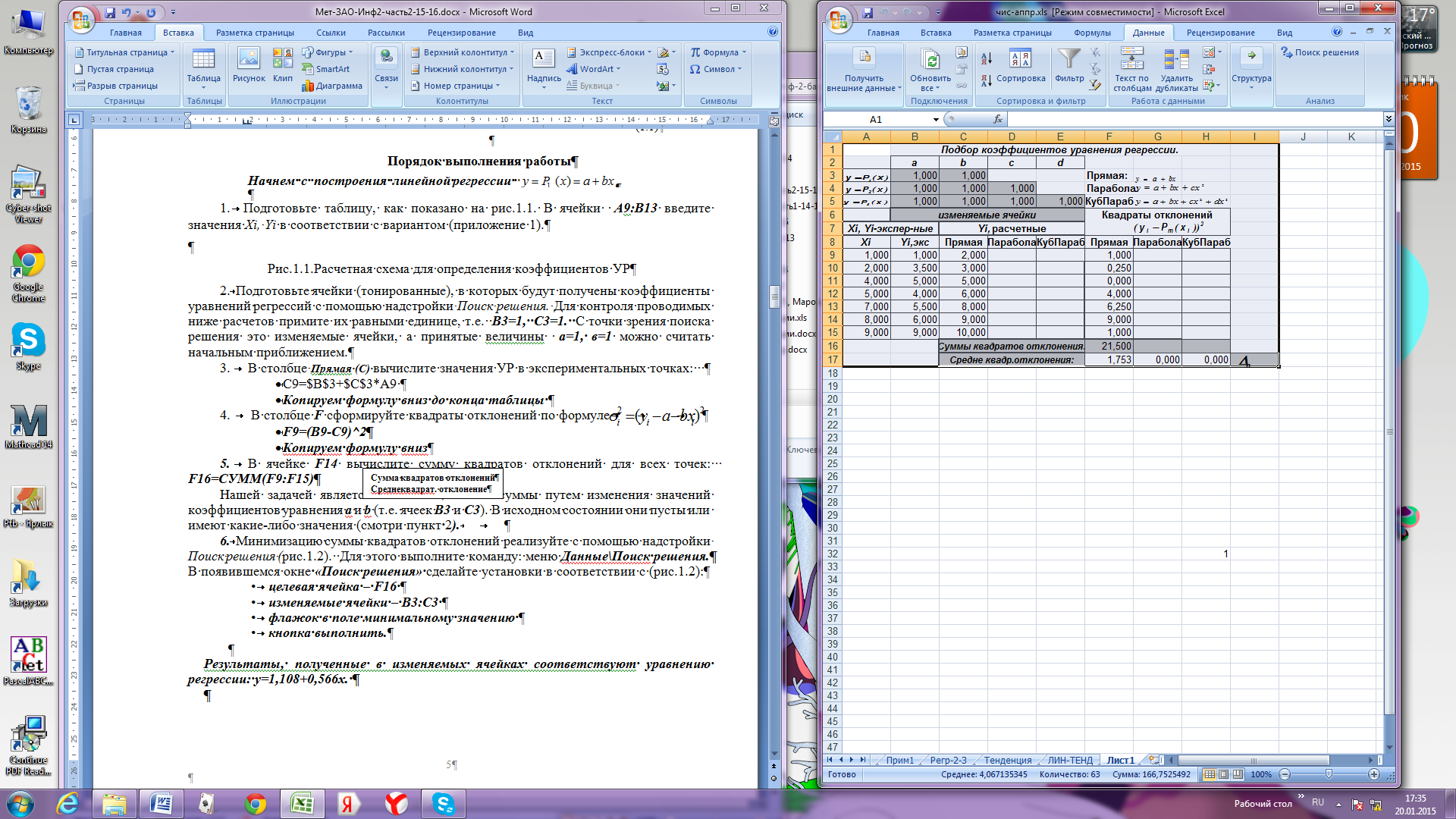
Рис.3.3. Расчетная схема для определения коэффициентов УР
4. В столбце F сформируйте квадраты отклонений по формуле 
· F9 =(B9-C9)^2
· Скопируйте формулу вниз
5. В ячейке F16 вычислите сумму квадратов отклонений для всех точек: F16=СУММ(F9:F15)
Нашей задачей (согласно методу наименьших квадратов) является минимизация этой суммы путем изменения значений коэффициентов a и b уравнения (т.е. ячеек В3 и С3). В исходном состоянии они пусты или имеют какие-либо значения (см. пункт2).
6. Минимизацию суммы квадратов отклонений будем производить с помощью надстройки Поиск решения. Для этого выполните команду: меню Данные\Анализ|Поиск решения.
В появившемся окне «Поиск решения» сделайте установки в соответствии с (рис.3.4):
• Установить целевую ячейку – F16
• Равной минимальному значению
• Изменяя ячейки – В3:С3
• Кнопка выполнить.
Рис.3.4. Окно Поиск решения. Определение коэффициентов
Результаты, полученные в изменяемых ячейках В3 и С3 соответствуют коэффициентам уравнения линейной регрессии y=1,108+0,566x
7. Аналогичным образом вычислите коэффициенты для УР 2-ого и 3-его порядков.
8. Вычислите средние квадратичные отклонения для каждого приближения по формуле (3.4):
• F17 = корень(F16/7) (7 – количество экспериментальных точек)
• Скопируйте формулу вправо
9. Сделайте обоснованный вывод о «наилучшем» приближении.
10. Постройте диаграммы всех аппроксимирующих функций, нанесите множество экспериментальных точек (рис.3.5).
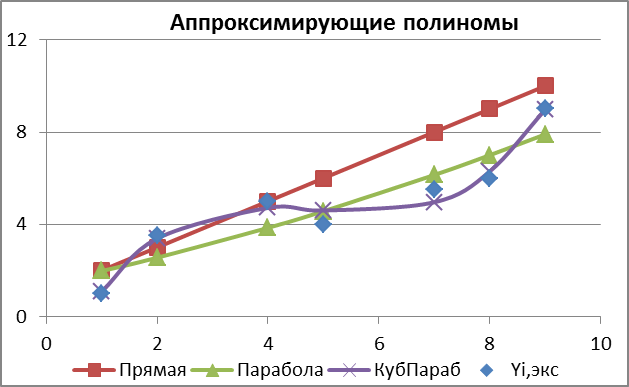
Рис.3.5. Аппроксимирующие полиномы и экспериментальные данные
11. Геометрический смысл степени точности аппроксимации проиллюстрируйте в соответствии с рис.3.6 для полученного вами наилучшего приближения.
Геометрический смысл степени точности аппроксимации иллюстрирует рис.3.6. Для этого строим график УР y= j (х), наносим экспериментальные точки Mi (xi, yi), i= 1,2 ,..,n. Добавляем еще два графика y= j (х)+ε и y= j (х) - ε. Если до 95% экспериментальных точек попадают в полосу шириной 2ε, т.е. отстоят от графика УР не далее чем на ε, то можно говорить о приближении с точностью ε.
Рис.3.6. Геометрический смысл степени точности аппроксимации
Проверьте правильность ваших расчетов, используя надстройку «Линия тренда».
Контрольные вопросы к индивидуальному заданию №3
1. Понятие аппроксимации (приближения). Когда возникают задачи аппроксимации.
2. Среднеквадратичное приближение. Суть метода наименьших квадратов (МНК).
3. Среднее квадратичное отклонение. Выбор «наилучшего» приближения.
4. Геометрический смысл точности аппроксимации исследуемого процесса.
Приложение 3
Варианты индивидуального задания 3
