Тема. Аппроксимация. Среднеквадратичное приближение функций
Задание 3. Оценить функциональную близость (в линейном смысле) значений результатов эксперимента x, y с помощью коэффициента корреляции R.
Построить аппроксимирующие функции, описывающие заданную зависимость, используя метод наименьших квадратов (МНК).
Порядок выполнения работы
В процессе эксперимента были получены результаты некоторой зависимости величины y от x (приложение 3, в соответствии с вариантом).
1. Вычислите коэффициент корреляции R (3.5). Оцените функциональную близость (в линейном смысле) значений результатов эксперимента x, y с помощью коэффициента корреляции R
2. В качестве аппроксимирующих функций возьмите уравнения регрессии (УР) (полиномы 1-й, 2-й и 3-й степени):
3. Вычислите параметры уравнений регрессий: a, b, c, d спомощью МНК.
4. Вычислите средние квадратичные отклонения для каждого УР. Сделайте обоснованный вывод о «наилучшем приближении».
5. Постройте графики всех аппроксимирующих функций и множество экспериментальных точек.
6. Проиллюстрируйте геометрический смысл точности аппроксимации соответствующим рисунком 3.6, выбрав в качестве аппроксимирующей функции «наилучшее» приближение
Теоретические сведения
«Аппроксимация (от лат. Approximo – приближаюсь) – это замена одних математических объектов другими, близкими к исходным »
Предположим, что при обработке результатов проведенного эксперимента обнаружена некая функциональная зависимость у=f(x) между независимой переменной х и зависимой переменной у. Эта зависимость представлена в виде табл. 3.1 значений xi, yi (i =1,2 ,…,n), полученных в ходе эксперимента.
Таблица 3.1
| у=f(x) | xi | x 1 | x 2 | … | xn |
| yi | y 1 | y 2 | … | yn |
Возникает вопрос: Всегда ли существует функциональная зависимость между экспериментальными данными, заданными таблицей 1, и каков вид этой зависимости.
Оценить функциональную близость (в линейном смысле) значений Х, У можно с помощью коэффициента корреляции R:
(3.5)
Если зависимость между х, у линейная (y=ax+b), то для
а>0 -.
а<0 -
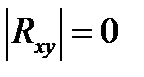При связь отсутствует
Принято считать:
R£0.3 – наблюдается слабая линейная связь,
R=0.3 – 0.7 – средняя,
R³0.7 –сильная,
R=1 – линейная зависимость, все точки лежат на одной прямой.
Таким образом, функция у=f(x) задана таблично (или графически), что создает определенные трудности при ее исследовании.
Возникает задача аппроксимации (замены) исследуемой зависимости у=f(x) аналитической функцией y= j (х) на отрезке [ x 1 ,xn ], т.е.
f(x)@ j (х). (3.1)
Аппроксимирующая функция y= j (х) называется уравнением регрессии (УР).
Геометрически задачапостроения уравнения регрессии состоит в проведении кривой L: y= j (х) «возможно ближе» примыкающей к системе экспериментальных точек Mi (xi, yi), i= 1,2 ,..,n, заданной табл. 3.1.
Уравнение регрессии записывается в виде многочлена (3.2), т.е. зависит от (m +1) параметра 
Параметры 
определяют расположение графика УР относительно экспериментальных точек Mi (xi, yi), i= 1,2 ,..,n (рис.3.1).
Рис. 3.1. Геометрический смысл задачи аппроксимации
Требуется подобрать параметры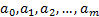 
так, чтобы график уравнения регрессии был расположен «как можно ближе» к системе экспериментальных точек.
Для нахождения параметров 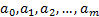используется метод наименьших квадратов.
Согласно методу наименьших квадратов (МНК) наилучшими параметрами  (i=0, 1,..., m) являются те, которые минимизирует сумму квадратов отклонений σi, т.е. функцию  :
где
|
Степень точности аппроксимации исследуемого процесса с помощью полученного УР может быть оценена величиной среднего квадратичного отклонения.
