1) Исходное уравнение преобразуем к виду x = φ(х):
| lnx-2+x=0 | Þ | C(lnx-2+x) + x = x | , |
т.е. φ(х) = C(lnx-2+x)+x;
2) Определим значение С, обеспечивающее сходимость вычислительного процесса метода простых итераций. Как видно из графика, полученного на этапе отделения корней, функция F(x) в точке пересечения с осью ОХ, т.е. в окрестности искомого корня уравнения, имеет нарастающий характер. Следовательно, параметр С должен находиться внутри промежутка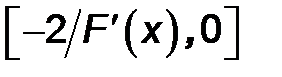 
.
Так как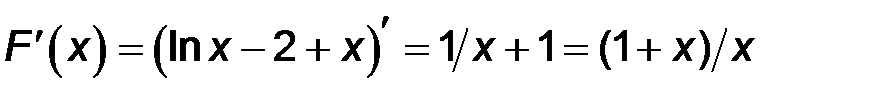 
, то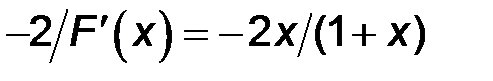 
. Вычислим эту величину для двух разных значений х=1,55 и х=1,90, полученных на этапе отделения корней, и обозначим полученные значения С1 и С2:
D15 Вычисление константы С
D16 C1= E16 =-2*A9/(1+A9) D17 C2 E17 =-2*A10/(1+A10)
Окончательное значение С определим как середину меньшего по длине интервала (С1, 0) или (С2, 0). В нашем случае это будет интервал (С1, 0): D18 C= E18 = E16/2.
3) Вносим заголовок таблицы метода простых итераций: D20 X D21 j(x) D22 R D23 N. Символ j можно получить по цепочке «Вставка→Символ».
4) Сформируем таблицу, реализующую вычислительный процесс метода простых итераций.
В качестве начального приближения возьмем одну из границ промежутка, найденного на этапе отделения корней, например, x0=1,90. В первую строку таблицы внесем:
D21 =A10 E21 =$E$18*(LN(D21)-2+D21)+D21 F21 =ABS(D21-E21) G21 0
В клетке D22 реализуем вычислительную формулу метода простых итераций x k=φ(x k-1): D22 =E21. Скопируем клетку E21 в E22.
Выполним вычисление ½xk - xk-1½: F22 =ABS(D22-D21).
Скопируем диапазон клеток D22: G22 на три-четыре или более строк ниже, пока в столбце F (R - ошибка, погрешность) не появится число, меньшее 0,0001. Соответствующее ему значение х (в нашем примере значение клетки D24) и будет решением задачи.
Окончательный вид EXCEL-таблицы приведен ниже:
| A | B | C | D | E | F | G | |
| Решение алгебраического уравнения lnx-2+x=0 | |||||||
| Иванов И.И., группа СВ-1ХХ | |||||||
| Отделение корней уравнения | |||||||
| Хn= | 0,5 | Хk= | 7,5 | H= | 0,35 | ||
| X | F(x) | ||||||
| 0,50 | -2,193147 | ||||||
| 0,85 | -1,312519 | ||||||
| 1,20 | -0,617678 | ||||||
| 1,55 | -0,011745 | ||||||
| 1,90 | 0,541854 | ||||||
| 2,25 | 1,060930 | ||||||
| 2,60 | 1,555511 | ||||||
| 2,95 | 2,031805 | ||||||
| 3,30 | 2,493922 | ||||||
| 3,65 | 2,944727 | Вычисление константы C | |||||
| 4,00 | 3,386294 | С1= | -1,215686 | ||||
| 4,35 | 3,820176 | С2= | -1,310345 | ||||
| 4,70 | 4,247563 | С= | -0,607843 | ||||
| 5,05 | 4,669388 | Уточнение корня | |||||
| 5,40 | 5,086399 | x | φ(x) | R | N | ||
| 5,75 | 5,499200 | 1,900000 | 1,570638 | 0,3293622 | |||
| 6,10 | 5,908289 | 1,570638 | 1,557193 | 0,0134458 | |||
| 6,45 | 6,314080 | 1,557193 | 1,557146 | 0,0000469 | |||
| 6,80 | 6,716923 | 1,557146 | 1,557146 | 0,0000001 | |||
| 7,15 | 7,117112 | ||||||
| 7,50 | 7,514903 | Результат: | х= | 1,557146 |
Результат решения:
- исходное уравнение lnx–2+x=0 преобразовано к виду x = С(lnx–2+x) + x, где С=-0,607843 обеспечивает сходимость вычислительного процесса;
- Fпри заданной точности ε=0,0001 определен корень исходного уравнения х=1,557146;
- это значение достигнуто на 3-й итерации.
