ТЕМА: Решение трансцендентных уравнений
Содержание документа:
| 3.1 | Задание | 1 |
| 3.2 | Краткие теоретические сведения | 2 |
| 3.3 | Пример выполнения задания в среде Excel | 4 |
| 3.4 | Пример выполнения задания в среде Mathcad | 9 |
| 3.5 | Контрольные вопросы | 10 |
| 3.6 | Таблица индивидуальных вариантов | 11 |
Задание.
Изучить теоретический и вспомогательный материал, изложенный в лекции «Решение трансцендентных уравнений» и в данных методических указаниях.
Задача 1. Средствами Excel выполнить отделение корней трансцендентного уравнения F (x)=0 на промежутке [ х н, х к]. Построить график функции F (x) на промежутке [ х н, х к].
Задача 2. Средствами Excel по результатам выполнения задачи 1 найти корни уравнения методом дихотомий или методом хорд и методом простых итераций.
ВНИМАНИЕ. Студенты подгрупп СВ-111 и СВ-121 выполняют решение задачи методом дихотомий, а студенты подгрупп СВ-112 и СВ-122– методом хорд. Кроме этого все студенты выполняют решение задачи методом простых итераций.
Задача 3. Используя результаты отделения корней решить заданное уравнение средствами Mathcad. Построить график функции F (x).
Для защиты задания представить на компьютере Excel- и Mathcad-файлы решения задачи и рукописный отчет. В отчете представить:
1) запись исходного уравнения F (x)=0и промежутка [ хн, хк ] поиска корня в соответствии с вариантом;
2) результат отделения корней;
3) значение корня уравнения и количество итераций для его достижения для значений точности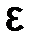 
=0.0001, полученные в среде Excel методом дихотомий или методом хорд;
4) преобразование исходного уравнения к виду, необходимому для использования метода простых итераций и выполнения условия сходимости метода;
5) значение корня уравнения и количество итераций для его достижения для значений точности 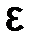=0.0001, полученные в среде Excel методом простых итераций;
6) значение корня уравнения с точностью до 5 дробных разрядов, полученное в среде Matcad;
7) ответы на контрольные вопросы.
Краткие теоретические сведения
Существует несколько различных методов численного решения трансцендентных уравнений, но все они предполагают выполнение двух этапов: первый из них называется " отделение корней ", второй - " уточнение корней ".
На этапе отделения корней определяются те интервалы заданного промежутка [ х нач, х кон], в каждом из которых расположен один и только один корень уравнения F (x)=0. Отделение корней можно выполнить с помощью следующих трех действий:
1) разбиение промежутка [ х нач, х кон] на некоторое количество частей с шагом h,
2) вычисление функции F (x) в точках разбиения,
3) выбор таких промежутков разбиения, на концах которых функция F (x) принимает значения разных знаков.
На этапе уточнения корней постановка задачи выглядит так: найти корень уравнения F (x)=0, содержащийся внутри интервала (А,В) с заданной точностью ε. Предполагается, что границы интервала (А,В) найдены на этапе отделения корней.
При уточнении корней методом дихотомий каждое новое приближение Р определяется как середина интервала (А, В), т.е.
.
Для дальнейшего приближения выбирается та половина (А, В), на концах которой F (x) имеет разные знаки. Алгоритм выбора нужной половинки (А, Р) или (Р, В) изображен на блок-схеме:
Если произведение значений F (А) и F (Р) отрицательное, то значит они имеют разные знаки, т.е. корень уравнения находится в половинке (А, Р) и, следовательно, точка B переносится в точку Р, в противном случае – в половинке (Р, В) и тогда точка А переносится в точку Р.
Критерием окончания итерационного процесса является выполнение неравенства
| В-А | < ε.
При уточнении корней методом хорд каждое новое приближение Р определяется как точка пересечения с осью ОХ прямой линии, соединяющей точки (А, F (A))и(B, F (В)), т.е.
.
Как и в методе дихотомий, для дальнейшего приближения выбирается тот отрезок (А, Р), или (Р, В), на концах которого F(x) имеет разные знаки. В зависимости от этого точка А или точка В переносится в точку Р. Критерием окончания итерационного процесса является выполнение неравенства
| Pk - Pk-1 | <ε,
где Pk-1, Pk -– два последовательных приближения к корню.
Для уточнения корней методом простых итерации необходимо исходное уравнение F (x)=0 преобразовать к эквивалентному уравнению x = φ (х). Тогда вычислительный процесс метода простых итераций выглядит так:
- выбираем начальное приближение x 0 как любую точку интервала (А, В);
- вычисляем значение φ (х 0) и называем его x 1, т.е. x 1 = φ (х 0);
- вычисляем значение φ (х 1) и называем его x 2, т.е. x 2 = φ (х 1);
Повторяя эту процедуру, будем иметь в общем виде на некотором k -м шаге:
x k = φ (x k-1).
При выполнении условия сходимости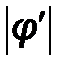 
<1 последовательность х 0, x 1, x 2,… x k, приближается к искомому корню.
Критерием окончания вычислительного процесса является выполнение неравенства ½ x k - x k-1½ < ε.
Сходимость метода простых итераций обеспечивается должным выбором преобразования уравнения F (x)=0 к виду x = φ (х). Существует более или менее универсальный способ преобразования:
| F (x) = 0 | Þ | C . F (x) = 0 | Þ | C . F (x) + x = x | , |
т.е. φ (х) выбирается в виде φ (х) = C . F (x) + x, а константа С определяется из условия сходимости метода.
Рассмотрим в общем виде процесс определения константы С. Если функция φ (х)= C . F (x)+ x, то условие сходимости метода простых итераций 
выглядит так: 
. Так как это неравенство содержит знак модуля, то оно распадается на два неравенства:
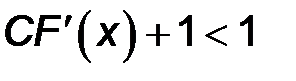 и
| 
|
или
 и
| 
|
При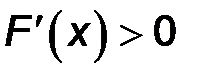 
получаем 
.
При 
получаем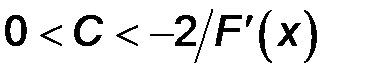 
.
Окончательное значение С выбирается как середина найденного интервала 
или 
.
Более подробную информацию о методе простых итераций и вопросах его сходимости, а также о других методах численного решения трансцендентных уравнений можно найти в лекции «Решение трансцендентных уравнений».
