Для установления на практике равномерной сходимости рядов пользуются достаточными признаками.
v Признак равномерной сходимости, основанный на сравнении функционального ряда со сходящимся числовым.
Теорема. Если члены ряда удовлетворяют неравенствам, где, а числа, не зависящие от, и, если ряд сходится, то ряд сходится равномерно на множестве X.
v Достаточные условия непрерывности суммы ряда.
Теорема. Если функции определены и непрерывны на множестве X и ряд сходится равномерно к сумме S(x), то эта сумма будет непрерывна на множестве X.
v Свойства равномерно сходящихся рядов.
Теорема. Если функции определены и непрерывны на отрезке и ряд сходится равномерно на к сумме, то его можно почленно интегрировать на этом отрезке
.
Теорема. Если функции определены на отрезке и существуют непрерывные производные на интервале, а ряд сходится на и равномерно сходится ряд, то сумма ряда имеет на интервале непрерывную производную, причем,.
Таким образом, ряд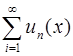 
можно почленно дифференцировать.
Степенной ряд
Степенным рядом называется ряд вида:
, (9)
где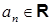 
‑ числовые коэффициенты, 
‑ фиксированное число и 
‑ переменная.
Если зафиксировать , то получится числовой ряд. Если этот числовой ряд сходится, то говорят, что степенной ряд (9) сходится в точке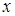 
. Множество всех точек , в которых ряд (9) сходится, называют множеством сходимости ряда (9).
Пример. Ряд 
сходится абсолютно при 
, т.к. 
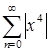при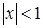 
сходится. Если же 
, то 
не стремится к нулю, т.е. не выполнено необходимое условие сходимости и ряд расходится. Таким образом, множеством сходимости ряда является 
.
Множество сходимости всякого ряда (9) есть промежуток, середина которого находится в точке 
. Промежуток сходимости может быть отрезком, полуинтервалом, интервалом, бесконечным промежутком или промежутком нулевой длины, т.е. точкой . Число 
, равное половине длины промежутка сходимости, называют радиусом сходимости. Радиус сходимости ряда (9) может быть вычислен следующим образом:
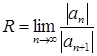, если такой предел существует;
1. 
, если такой предел существует.
Если в формулах 2. и 3. пределы равны 0, то 
. Если пределы равны 
, то 
.
Если ‑ конечное число, то промежуток 
принадлежит множеству сходимости. В ряде случаев множеству сходимости могут принадлежать также точки 
и 
.
Пример. Ряд 
имеет радиус сходимости 
.
Значит, интервал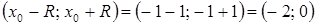 
входит в промежуток сходимости. Исследуем сходимость ряда на концах интервала 
. При 
получаем ряд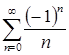 
, который сходится по признаку Лейбница. При 
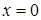получаем ряд 
, который расходится. Таким образом, промежуток сходимости ряда – полуинтервал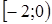 
.
Пример. Ряд 
имеет радиус сходимости 
. Значит, интервал сходимости 
.
Изучим сходимость ряда на концах этого интервала. При получаем ряд 
, который сходится абсолютно. При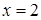 
получаем ряд 
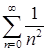, который также сходится. Значит, промежуток сходимости – отрезок 
.
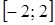Если функция 
в точке имеет производные любого порядка, то для нее можно построить степенной ряд:
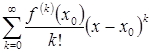(10)
Этот ряд называется рядом Тейлора для функции в точке .
Множество сходимости ряда (10) не всегда совпадает с областью определения функции , а его сумма не обязательно равна . Если сумма ряда (10) совпадает с на множестве 
, то можно написать:
(11)
В этом случае говорят, что на множестве разложена в степенной ряд (11). Справедливы следующие разложения:
, .
,
, .
, 
.
, .
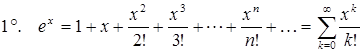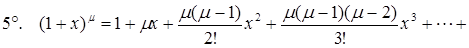
При разложении функций в степенные ряды бывает удобным использовать разложения 
.
Пример. Разложить по степеням 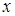функцию 
.
Если обозначить 
, то, используя разложение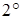 
, получаем: 
.
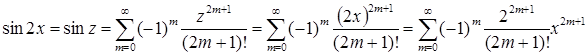Поскольку разложение 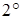справедливо для , то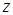 
может быть любым действительным числом.
Пример. Разложить по степеням 
функцию 
.
Обозначив 
и использовав разложение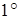 
, получим 
.
Это разложение справедливо для 
, поскольку 
может быть любым числом.
Ряды Фурье
Рассмотрим функциональные ряды, суммы которых, в отличие от степенных рядов, имеют непустое конечное множество точек разрыва в области задания.
Функция называется кусочно-непрерывной на отрезке 
, если она непрерывна всюду, кроме конечного числа точек разрыва первого рода. Другими словами, область ее определения можно разбить на конечное число частичных отрезков 
, на каждом из которых:
1. функция 
ограничена и непрерывна во внутренних точках;
2. На концах каждого отрезка существуют конечные односторонние пределы 
, 
.
Под интегралом функции понимается число 
.
Можно доказать, что для кусочно-непрерывной на отрезке функции существует обобщенная первообразная 
(
, 
), и, следовательно, 
.
Функция называется кусочно-дифференцируемой (или кусочно-гладкой) на , если производная 
кусочно-непрерывна на отрезке .
Пусть функции 
и 
кусочно-непрерывны на отрезке . Скалярное произведение этих функций можно определить как 
.
Можно показать, что произведение двух кусочно-непрерывных на отрезке функций есть функция кусочно-непрерывная на этом отрезке и, следовательно, ее определенный интеграл на этом отрезке существует.
Тогда 
, 
.
Число 
называется нормой функции .
Очевидны свойства скалярного произведения:
1. 
– свойство коммутативности или симметрии;
2. 
– свойство ассоциативности или сочетательности;
3. 
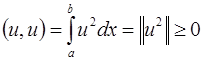, причем 
.
Функции 
и 
называются ортогональными, если 
, при этом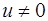 
, 
.
Рассмотрим основную систему тригонометрических функций общего периода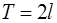 
:
.
Функции 
, 
и 
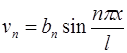, называются основными гармониками. Их графиками являются синусоиды с амплитудами соответственно 
и 
. Гармоника 
и поэтому не рассматривается.
Лемма. Основные тригонометрические функции попарно ортогональны на любом промежутке, длина которого равна общему периоду 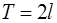этих функций, т.е. для стандартного отрезка 
справедливы условия ортогональности:
I. 
при 
;
II. 
при ;
III. 
.
Условия ортогональности проверяются непосредственным интегрированием, в ходе которого используются формулы тригонометрии:
1) 
;
2) 
;
3) 
.
Например, при :
1) 
,
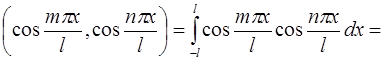
т.к.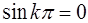 
при целых значениях 
;
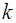2) 
;
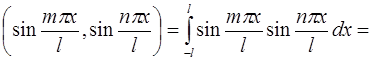
3) 
Пусть – кусочно-непрерывная периодическая функция периода .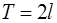
Можно попытаться провести т.н. гармонический анализ , т.е. представить эту функцию в виде суммы конечного или бесконечного числа гармоник того же периода :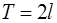
,
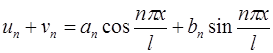Таким образом, можно прийти к тригонометрическому ряду Фурье:
.
Коэффициент нулевой гармоники обычно берется с множителем 
.
Исторически эта задача впервые возникла при математической обработке результатов наблюдения высоты приливной волны, которая периодически повторяется с течением времени. Гармонический анализ высоты приливной волны позволил дать долгосрочные предсказания ее величины, что было весьма важно для мореплавателей.
Предположим, что ряд:
сходится на отрезке и допускает почленное интегрирование, в результате которого получится следующее:
Так как из условий ортогональности:
при 
, то получается
.
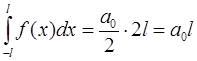Отсюда: 
.
Интересно отметить, что свободный член тригонометрического ряда Фурье 
представляет собой среднее значение периодической функции .
Если умножить левую и правую части ряда на 
и почленно проинтегрировать, то получится:
.
Предварительно, следует отметить, что:
,
т.е. 
.
Отсюда, в силу условий ортогональности, а также с учетом нормировки, получается:
.
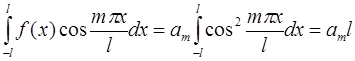Следовательно: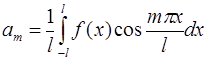 
, а значит, заменяя 
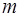на 
(что по смыслу формул допустимо), можно получить:
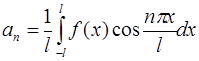
Аналогично, умножая обе части ряда на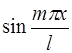 
и почленно интегрируя, получим:
.
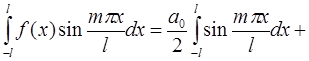
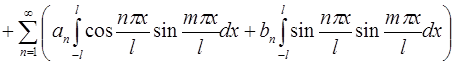В данном случае условие нормировки:
,
т.е. 
.
В силу условий ортогональности:
Следовательно, 
, а значит:
.
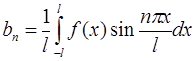Числа и называются коэффициентами Фурье функции .
Тригонометрический ряд:
,
коэффициентами которого являются коэффициенты Фурье данной периодической функции называется ее тригонометрическим рядом Фурье, независимо от того, будет ли сумма этого ряда равна функции или нет. В последнем случае говорят, что функция порождает ряд Фурье:
,
где знак ~ означает «соответствует».
Теорема сходимости. Пусть периодическая функция, определенная на, кроме, может быть, точек ее разрывов, и имеющая период, является кусочно–дифференцируемой (или кусочно–гладкой) на любом промежутке, длина которого равна периоду этой функции.
Тогда:
1. Ее тригонометрический ряд Фурье сходится для любого значения 
, т.е. существует сумма ряда Фурье
;
2. Сумма ряда Фурье 
равна функции в точках 
ее непрерывности = и равна среднему арифметическому пределов функции слева и справа в точках 
разрыва функции, т.е.:
Поскольку, для точек непрерывности функции можно записать 
, то в общем случае:
.
Таким образом, для тригонометрического ряда Фурье функции имеем:
,
где коэффициенты и определяются по формулам:
.
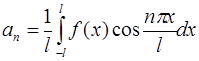
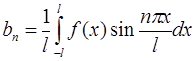Если принять, что период функции равен 
, т.е. 
, то расчетные формулы значительно упрощаются:
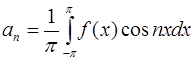
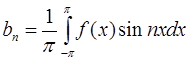
где .
