55. Определение производной функции у = f (х).
56. Теорема о непрерывности дифференцируемой функции.
57. Таблица производных основных элементарных функций.
58. Правила дифференцирования суммы, произведения и частного функций.
59. Теорема о дифференцировании сложной функции.
60. Правило дифференцирования обратной функции.
61. Геометрический смысл производной функции у = f (х).
62. Уравнение касательной к графику функции у = f (х).
63. Определение дифференциала функции у = f (х).
64. Условие существования дифференциала функции у = f (х).
65. Формула вычисления дифференциала функции у = f (х).
66. Понятие производных и дифференциалов высших порядков функции у = f (х).
67. Условие монотонности функции у = f (х) (через производную).
68. Теорема Ферма об обращении в нуль производной в точке наибольшего (наименьшего) значения функции.
69. Определение точки экстремума функции у = f (х).
70. Необходимое условие экстремума функции у = f (х).
71. Достаточные условия экстремума функции у = f (х) через первую производную.
72. Достаточные условия экстремума функции у = f (х) через вторую производную.
73. Теорема Ролля об обращении производной в нуль, ее геометрический смысл.
74. Теорема Лагранжа об отношении  , ее геометрический смысл.
, ее геометрический смысл.
75. Правило Лопиталя раскрытия неопределенности 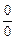 .
.
76. Правило Лопиталя раскрытия неопределенностей 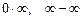 .
.
77. Правило Лопиталя раскрытия неопределенностей  .
.
78. Определение выпуклости вверх и выпуклости вниз графика функции у = f (х).
79. Необходимые и достаточные условия выпуклости вниз (вверх) графика функции у = f (х).
80. Понятие точки перегиба.
81. Необходимые и достаточные условия существования точек перегиба.
82. Понятие асимптоты графика функции.
83. Условие существования и уравнение вертикальной асимптоты.
84. Условие существования и уравнение горизонтальной асимптоты.
85. Условие существования и уравнение наклонной асимптоты.
86. Определение частных производных функций нескольких переменных.
87. Понятие частных производных высших порядков.
88. Условие равенства смешанных частных производных.
89. Определение дифференциала функции нескольких переменных.
90. Формула вычисления дифференциала функции нескольких переменных.
91. Формулы вычисления дифференциала второго порядка функции z = f (х, y).
92. Определение точек экстремума функции у = f (х 1, x 2,…, xn).
93. Необходимое условие экстремума для функций у = f (х 1, x 2,…, xn).
94. Достаточные условия экстремума функций у = f (х 1, x 2,…, xn).
95. Понятие условного экстремума.
96. Метод Лагранжа отыскания условного экстремума.
Интегральное исчисление
97. Определение первообразной функции.
98. Соотношение между двумя первообразными функции у = f (х).
99. Определение неопределенного интеграла функции у = f (х).
100. Свойства неопределенного интеграла.
101. Таблица интегралов.
102. Вычисление интегралов подведением функции под знак дифференциала.
103. Формула интегрирования по частям.
104. Замена переменной в неопределенном интеграле.
105. Интегрирование простых дробей.
106. Вычисление интегралов от рациональных функций.
107. Определение определенного интеграла функции у = f (х).
108. Свойства определенного интеграла.
109. Интеграл с переменным верхним пределом.
110. Формула Ньютона-Лейбница вычисления определенного интеграла функции у = f (х).
111. Замена переменной в определенном интеграле.
112. Геометрический смысл определенного интеграла.
113. Вычисление площади криволинейной трапеции в декартовой системе координат, если границы области заданы явно.
114. Вычисление площади криволинейной трапеции в декартовой системе координат, если граница области задана параметрически.
115. Вычисление площади криволинейного сектора, если границы области заданы в полярной системе координат.
116. Вычисление длины дуги кривой, если кривая задана явно.
117. Вычисление длины дуги кривой, если кривая задана параметрически.
118. Вычисление длины дуги кривой, если кривая задана в полярной системе координат.
119. Определение несобственного интеграла 1-го рода.
120. Признак сравнения сходимости несобственного интеграла 1-го рода.
121. Сходимость интеграла  .
.
122. Определение несобственного интеграла 2-го рода.
123. Признак сравнения сходимости несобственного интеграла 2-го рода.
124. Сходимость интеграла  в случае, когда
в случае, когда  .
.
127. Понятие двойного интеграла.
128. Свойства двойного интеграла.
129. Понятие повторного интеграла.
130. Вычисление двойного интеграла в декартовой системе координат.
131. Замена переменных в двойном интеграле.
132. Переход в двойном интеграле к полярной системе координат.
133. Вычисление площади с помощью двойного интеграла.






