Пределы, производные и приложения производной функций.
А = 0, В = 1, из таблиц находим, что т =1, п =5.
2.1.1 Найти пределы функций:
а) 
;
б) 
;
в)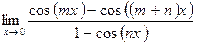 
;
Производные функций.
2.1.2 Найти производные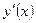 
функций:
а) 
; 
б)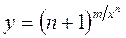 
; 
в) 
; 
д) 
Приложения производной.
m=1 n=5
С помощью методов дифференциального исчисления построить график функции:
Функция определена на 
Не периодична. Не является ни четной, ни нечетной.
Пересекается с осью х в одной точке х=1/5, с осью y в точке y=1/25.
Исследуем на непрерывность:
Функция имеет две вертикальные асимптоты x=-5 и x=5.
и 
Функция имеет общую горизонтальную асимптоту y=0.
Возьмем производные:
Очевидно, что первая производная отрицательная на всем множестве существования функции. Функция убывает везде, где существует.
. У второй производной есть только один действительный корень, равный 
.
Для построения графика знаки производных в характерных точках и промежутках сведем в таблицу:
| x | (-∞;-5) | -5 | (-5;x3) | x3 | (x3;5) | (5;+ ∞) | |
| y | нет | нет | |||||
| - | нет | - | - | - | нет | - |
| - | нет | + | - | нет | + | |
| Убывает. выпукла вверх | Верт. ассимпт. | Убывает. выпукла вниз | перегиб | Убывает. выпукла вверх | Верт. ассимпт. | Убывает. выпукла вниз |
Построим график функции:
Функции нескольких переменных
Частные производные и дифференциал функции.
3.1.1 Найти частные производные 
, 
и 
функций:
m=1 n=5
а) 
;
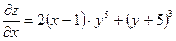
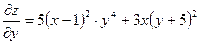
б) 
3.1.2 Найти полный дифференциал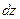 
функции 
.
Приложения частных производных.
3.2.1 Для функции 
в точке 
найти градиент и построить вектор градиента. A(-5;1)
Числовые данные параметров т и п в контрольной работе №1 определяются по двум последним цифрам своей зачетки (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | ||||||||||
| т |
Таблица 2 (выбор параметра п)
| В | ||||||||||
| п |
A=0 b=1 -à m=1 n=5
Неопределенный интеграл.
Найти интегралы:
а) 
б) 
в) 
г) 
;
Этот пример лучше решить предварительно решив задачу о нахождении интеграла по частям два раза:
Сначала найдем интеграл:
Теперь найдем второй интеграл:
Теперь найдем наш интеграл (просто подставим a=1 b=1 alpha=5):
Определенный интеграл
Вычислить определенный интеграл
а) 
; б) 
;
в) 
; г) 
m=1 n=5
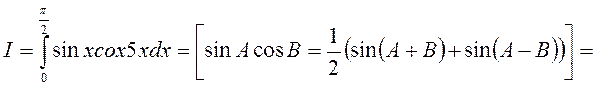
Второе слагаемое равно нулю, так как синус интегрируется на длине периода. Следовательно:
Сначала найдем интеграл:
Теперь найдем наш интеграл:
Несобственные интегралы.
Вычислить интеграл или установить его расходимость:
а)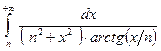 
б) 
m=1 n=5
сходится.
0 преподаватель должен более внимательно составлять задание!
