Линейная алгебра
Действия с матрицами.
Выполнить действия: m=1 n=5
а) 
; 
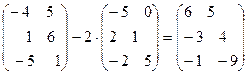
б) 
. 
Вычисление определителей.
Вычислить определитель 
двумя способами:
а) по правилу «треугольников»; б) по правилу Сарруса
а) по правилу «треугольников» 
0+(-150)+(-2)-0-20-12=-184.
б) по правилу Сарруса
Заметим, что это одно и тоже – поэтому так больше вычислять не будем.
Самым эффективным методом вычисления определителей 3-го и более порядка с целыми числами является применение свойств определителя, позволяющее обнулять его элементы с последующим разложением по разреженной строке (столбцу).
Умножим первый столбик на 6 и сложим с последним:
Системы линейных уравнений.
Решить систему уравнений методом Гаусса. Сделать проверку.
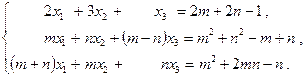Решим систему методом Гаусса с модификацией Жордана и с контрольным столбцом:
Проверка.
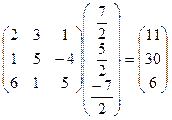
Примеры решения некоторых задач.
1. Даны два вектора 
и 
Найти их модули, скалярное произведение и cos угла между ними.
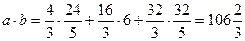
2. Решить систему
а. метод Крамера.
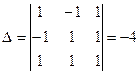
Следовательно, 
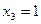
б. Метод Гаусса.
в. Метод обратной матрицы.
Найдем обратную по отношению к матрице системы матрицу методом Гаусса-Жордана.
Таким образом, обратная матрица вычислена и равна 
Решение получим умножением обратной матрицы на столбец правых частей:
3.Решить систему методом Гаусса 
Здесь мы 
поменяли второй и четвертый столбцы. Теперь неизвестные идут в таком порядке:
Теперь выпишем решение: 
или 
Привести 
к каноническому виду.
Заменим переменные по формулам: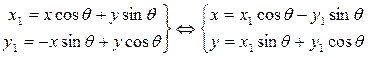 
Приведем подобные:
Для обнуления члена, содержащего 
решим уравнение
и найдем угол поворота 
. Тогда, подставив значение этого угла в уравнение, найдем:
или 
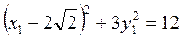или 
или 
Получили уравнение эллипса.
Вычислить определитель 
Умножим третью строку на -1 и сложим счетвертой:
Умножим четвертую строку на -1 и сложим с пятой: 
Теперь умножим пятую строку на -1 и сложим с шестой: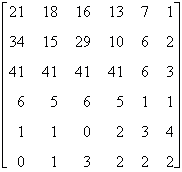 
Теперь будем умножать четвертую строку на -7, -5, -3 и складывать соответственно с третьей, второй и первой строками: 
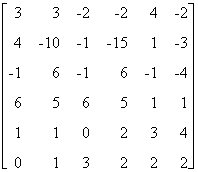Получили определитель, содержащий не такие большие целые числа, как в первоначальном виде. Оставим пятую строчку неизменной, но умножая ее на необходимые множители будем складывать полученную с другими строками, чтобы получить нули в первом столбце: 
Разлагая этот определитель по первому столбцу, получим: 
Здесь мы учитывали, что алгебраическое дополнение имеет множитель -1 или 1 в зависимости от нечетности или четности суммы номера строки и номера столбца ненулевого элемента столбца разложения, а сам элемент равен единице. Оставим пятую строчку неизменной, но умножая ее на необходимые множители будем складывать полученную с другими для получения нулей в четвертом столбце: 
Разлагая определитель по первому столбцу, получим: 
Здесь мы также учитывали, что алгебраическое дополнение имеет множитель -1 или 1 в зависимости от нечетности или четности суммы номера строки и номера столбца ненулевого элемента столбца разложения, а сам элемент равен единице. Из третьей строки вынесем 2 и получим: 
Умножим третий столбец на -1 и сложим с четвертым, чтобы получить единицу: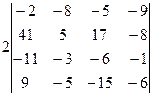 
Оставим третью строчку неизменной, но умножая ее на необходимые множители будем складывать полученную с другими для получения нулей в четвертом столбце: 
Разлагая полученный определитель по четвертому столбцу, получим: 
Здесь мы учитывали, что алгебраическое дополнение имеет множитель -1 или 1 в зависимости от нечетности или четности суммы номера строки и номера столбца ненулевого элемента столбца разложения, а сам элемент равен минус единице. Сумма в данном случае нечетная = 3+4. Второй столбец, оставляя неизменным, умножим на -5 и сложим с первым, а также умножим на -2 и сложим с третьим: 
Вынесем множитель 2 из первого столбца и получим: 
Умножим первую строку на 8 и на -5 и сложим со второй и третьей соответственно: 
Вынесем -2 из третьей строки: 
Разложим определитель по первому столбцу и вычислим его: 
280
6. Пусть 
Тогда, применяя уже продемонстрированный на задании 2. метод Гаусса-Жордана, вычислим обратную матрицу:
Полином 
при 
будет вычисляться так: 
