Обозначим через  частичные суммы ряда Фурье функции
частичные суммы ряда Фурье функции  :
:
 .
.
Далее обсуждается сходимость последовательности функций  к функции
к функции  в различных смыслах. Функция
в различных смыслах. Функция  предполагается
предполагается  -периодической (если она задана только на промежутке
-периодической (если она задана только на промежутке  , её можно периодически продолжить).
, её можно периодически продолжить).
- Если
 , то последовательность
, то последовательность  сходится к функции
сходится к функции  в смысле
в смысле  . Кроме того,
. Кроме того,  являются наилучшим (в смысле расстояния в
являются наилучшим (в смысле расстояния в  ) приближением функции
) приближением функции  тригонометрическим многочленом степени не выше
тригонометрическим многочленом степени не выше  .
. - Сходимость ряда Фурье в заданной точке
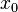 — локальное свойство, то есть, если функции
— локальное свойство, то есть, если функции  и
и  совпадают в некоторой окрестности
совпадают в некоторой окрестности 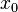 , то последовательности
, то последовательности 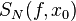 и
и 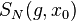 либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают. (Принцип локализации)
либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают. (Принцип локализации) - Если функция
 дифференцируема в точке
дифференцируема в точке 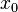 , то её ряд Фурье в этой точке сходится к
, то её ряд Фурье в этой точке сходится к 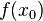 . Более точные достаточные условия в терминах гладкости функции
. Более точные достаточные условия в терминах гладкости функции  задаются признаком Дини.
задаются признаком Дини. - Функция, непрерывная в точке
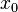 , может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к
, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к 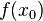 . Это следует из того, что для непрерывной в
. Это следует из того, что для непрерывной в 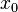 функции
функции  последовательность
последовательность 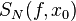 сходится по Чезаро к
сходится по Чезаро к 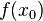 .
. - Если функция
 разрывна в точке
разрывна в точке 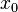 , но имеет пределы в этой точке справа и слева
, но имеет пределы в этой точке справа и слева 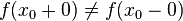 , то при некоторых дополнительных условиях
, то при некоторых дополнительных условиях 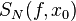 сходятся к
сходятся к 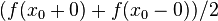 . Подробнее см. модифицированный признак Дини.
. Подробнее см. модифицированный признак Дини. - Теорема Карлесона: если
 , то её ряд Фурье сходится к ней почти всюду. Это верно и если
, то её ряд Фурье сходится к ней почти всюду. Это верно и если 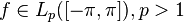 . Однако, существуют функции из
. Однако, существуют функции из  , ряд Фурье которых расходится во всех точках (теорема Колмогорова).
, ряд Фурье которых расходится во всех точках (теорема Колмогорова). - Зафиксируем точку
 . Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве
. Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве  . В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.
. В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.
6.Гельдера условие.



Пространство Лебега.






Неравенства Гельдера.
Определение 1. Класс функций, интегрируемых по Лебегу со степенью  , обозначается
, обозначается 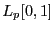 (
( ) включает в себя функции
) включает в себя функции  такие, что
такие, что  . Если
. Если 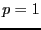 , то обозначают
, то обозначают  . Поэтому полагают
. Поэтому полагают  .
.
Замечание 1. Покажем, что если 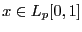 и
и  , то
, то 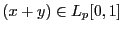 . Для этого докажем
. Для этого докажем  . Полагая т
. Полагая т  для определенности, имеем
для определенности, имеем 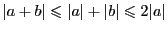 , откуда
, откуда  . Тогда можно получить аналогичное неравенство и для значений функций:
. Тогда можно получить аналогичное неравенство и для значений функций:  . Рассматривая интегралы левой и правой частей неравенства, получим сходимость интеграла левой части, что доказывает требуемое.
. Рассматривая интегралы левой и правой частей неравенства, получим сходимость интеграла левой части, что доказывает требуемое.
Лемма 1. Для любых 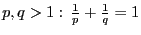 выполнено
выполнено 
Доказательство. Положим  . Рассмотрим график функции
. Рассмотрим график функции  , отметим на оси
, отметим на оси  точку
точку  , а на оси
, а на оси  точку
точку  . Рассматривая соотношение площадей, можем заключить
. Рассматривая соотношение площадей, можем заключить  . Эти же площади легко вычислить как площади под графиком функции, т.е. с помощью интегралов. Соответствующие выражения:
. Эти же площади легко вычислить как площади под графиком функции, т.е. с помощью интегралов. Соответствующие выражения:

Обозначая  , получим требуемое.
, получим требуемое. 
Определение 2. Числа  большие
большие 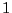 такие, что
такие, что 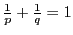 будем называть сопряженными показателями.
будем называть сопряженными показателями.
Предложение 1. (Неравенство Гельдера) Пусть  , где
, где  -- сопряженные показатели. Тогда
-- сопряженные показатели. Тогда

Доказательство. Положим  . По лемме получим:
. По лемме получим:
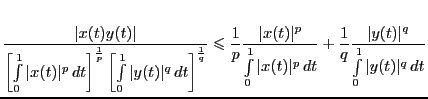
Интегрируя полученное неравенство и вспоминая соотношение для сопряженных показателей, получим требуемое неравенство. 
Замечание 2. При 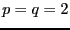 получается неравенство Буняковского.
получается неравенство Буняковского.
Лемма 2. Пусть  . Тогда
. Тогда  .
.
Доказательство. Рассмотрим  . Учитывая, что
. Учитывая, что  , получим, что интеграл равен
, получим, что интеграл равен  , тогда по определению
, тогда по определению  .
. 
Гильбертово пространство
Гильбертово пространство — обобщение евклидова пространства, допускающее бесконечную размерность. Названо в честь Давида Гильберта.
Гильбертово пространство — линейное (векторное) пространство (над полем вещественных или комплексных чисел), в котором для любых двух элементов пространства  и
и  определено скалярное произведение
определено скалярное произведение  , и которое является полным относительно порождённой этим скалярным произведением метрики
, и которое является полным относительно порождённой этим скалярным произведением метрики  . Если условие полноты пространства не выполнено, то говорят о предгильбертовом пространстве. Однако, большинство из известных (используемых) пространств либо являются полными, либо могут быть пополнены.
. Если условие полноты пространства не выполнено, то говорят о предгильбертовом пространстве. Однако, большинство из известных (используемых) пространств либо являются полными, либо могут быть пополнены.
Таким образом, гильбертово пространство есть банахово пространство (полное нормированное пространство), норма которого порождена положительно определённым скалярным произведением и определяется как 
Норма в произвольном нормированном пространстве может порождаться некоторым скалярным произведением тогда и только тогда, когда выполнено следующее равенство (тождество) параллелограмма:

Если удовлетворяющее тождеству параллелограмма банахово пространство является вещественным, то отвечающее его норме скалярное произведение задаётся равенством

Если это пространство является комплексным, то отвечающее его норме скалярное произведение задаётся равенством
 (поляризационное тождество).
(поляризационное тождество).
ПРИМЕР.
- Евклидово пространство.
- Пространство
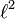 . Его точки суть бесконечные последовательности вещественных чисел
. Его точки суть бесконечные последовательности вещественных чисел  , для которых сходится ряд
, для которых сходится ряд  . Скалярное произведение на этом пространстве задаётся равенством
. Скалярное произведение на этом пространстве задаётся равенством
 .
.
- Пространство
 измеримых функций с вещественными значениями на отрезке
измеримых функций с вещественными значениями на отрезке  с интегрируемыми по Лебегу квадратами — то есть таких, что интеграл
с интегрируемыми по Лебегу квадратами — то есть таких, что интеграл

определён и конечен, притом функции, отличающиеся между собой на множестве мере нуль — отождествляются между собой (то есть, формально,  есть соответствующее множество классов эквивалентностей). Скалярное произведение на этом пространстве задаётся равенством
есть соответствующее множество классов эквивалентностей). Скалярное произведение на этом пространстве задаётся равенством
 .
.
Для пространств 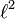 и
и  над полем комплексных чисел, последовательностей комплексных чисел и комплекснозначных функций, определение скалярного произведения отличается лишь комплексной сопряжённостью второго сомножителя:
над полем комплексных чисел, последовательностей комплексных чисел и комплекснозначных функций, определение скалярного произведения отличается лишь комплексной сопряжённостью второго сомножителя:
 ;
;
 .
.
Банахово пространство.
Банахово пространство — нормированное векторное пространство, полное по метрике, порождённой нормой. Основной объект изучения функционального анализа. Названо по имени польского математика Стефана Банаха (1892—1945), который с 1922 года систематически изучал эти пространства, используя введённую им аксиоматику.
Пример.
Некоторые примеры банаховых пространств (далее через  обозначено одно из полей
обозначено одно из полей  или
или  ):
):
- Евклидовы пространства
 с евклидовой нормой, определяемой для
с евклидовой нормой, определяемой для  как
как 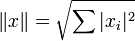 , являются банаховыми пространствами.
, являются банаховыми пространствами. - Пространство всех непрерывных функций
 , определённых на закрытом интервале
, определённых на закрытом интервале  будет банаховым пространством, если мы определим его норму как
будет банаховым пространством, если мы определим его норму как  . Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как
. Такая функция будет нормой, так как непрерывные функции на закрытом интервале являются ограниченными. Пространство с такой нормой является полным, а полученное банахово пространство обозначается как  . Этот пример можно обобщить к пространству
. Этот пример можно обобщить к пространству  всех непрерывных функций
всех непрерывных функций  , где
, где  — компактное пространство, или к пространству всех ограниченных непрерывных функций
— компактное пространство, или к пространству всех ограниченных непрерывных функций  , где
, где  — любое топологическое пространство, или даже к пространству
— любое топологическое пространство, или даже к пространству  всех ограниченных функций
всех ограниченных функций  , где
, где  — любое множество. Во всех этих примерах мы можем перемножать функции, оставаясь в том же самом пространстве: все эти примеры являются банаховыми алгебрами.
— любое множество. Во всех этих примерах мы можем перемножать функции, оставаясь в том же самом пространстве: все эти примеры являются банаховыми алгебрами. - Если
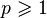 — вещественное число, то пространство всех бесконечных последовательностей
— вещественное число, то пространство всех бесконечных последовательностей  элементов из
элементов из  , таких что ряд
, таких что ряд 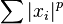 сходится, является банаховым относительно нормы, равной корню степени
сходится, является банаховым относительно нормы, равной корню степени  из суммы этого ряда, и обозначается
из суммы этого ряда, и обозначается  .
. - Банахово пространство
 состоит из всех ограниченных последовательностей элементов из
состоит из всех ограниченных последовательностей элементов из  ; норма такой последовательности определяется как точная верхняя грань абсолютных величин (модулей) элементов последовательности.
; норма такой последовательности определяется как точная верхняя грань абсолютных величин (модулей) элементов последовательности. - Снова, если
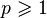 — вещественное число, можно рассматривать все функции интегрируемыми по Лебегу. Корень степени
— вещественное число, можно рассматривать все функции интегрируемыми по Лебегу. Корень степени  этого интеграла определим как норму
этого интеграла определим как норму  . Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом:
. Само собой, это пространство не будет банаховым, поскольку есть ненулевые функции, чья норма будет равна нулю. Определим отношение эквивалентности следующим образом:  и
и  эквивалентны тогда и только тогда, когда норма
эквивалентны тогда и только тогда, когда норма  равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как
равна нулю. Множество классов эквивалентности тогда является банаховым пространством; оно обозначается как  . Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например, Lp-пространства.
. Важно использовать именно интеграл Лебега, а не интеграл Римана, поскольку интеграл Римана не порождает полное пространство. Эти примеры можно обобщить. См., например, Lp-пространства. - Если
 и
и  — банаховы пространства, то можно составить их прямую сумму
— банаховы пространства, то можно составить их прямую сумму  , которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств.
, которая опять-таки будет банаховым пространством. Можно и обобщить этот пример к прямой сумме произвольно большого числа банаховых пространств. - Если
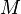 — замкнутое подпространство банахова пространства
— замкнутое подпространство банахова пространства  , то факторпространство
, то факторпространство  снова является банаховым.
снова является банаховым. - Любое гильбертово пространство тоже является банаховым. Обратное неверно.
- Если
 и
и 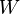 — банаховы пространства над одним полем
— банаховы пространства над одним полем  , тогда множество непрерывных
, тогда множество непрерывных  -линейных отображений
-линейных отображений  обозначается
обозначается  . Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными.
. Заметим, что в бесконечномерных пространствах не все линейные отображения автоматически являются непрерывными.  — векторное пространство, и, если норма задана как
— векторное пространство, и, если норма задана как  , является также и банаховым.
, является также и банаховым. - Пространство
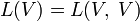 представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений
представляет собой унитарную банахову алгебру; операция умножения в ней задаётся как композиция линейных отображений
11.Базис,ортогональный базис. 


12.Линейно зависимые и линейно независимые системы векторов.

Интеграл Лебега
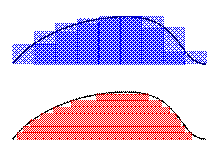
Сверху интегрирование по Риману, снизу по Лебегу
Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций.
Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману.
Определение
Интеграл Лебега определяют пошагово, переходя от более простых функций к сложным. Будем считать, что дано пространство с мерой 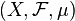 , и на нем определена борелевская функция
, и на нем определена борелевская функция  .
.
Определение 1. Пусть  — индикатор некоторого измеримого множества, то есть
— индикатор некоторого измеримого множества, то есть  , где
, где  . Тогда интеграл Лебега функции
. Тогда интеграл Лебега функции  по определению:
по определению:

Определение 2. Пусть  — простая функция, то есть
— простая функция, то есть  , где
, где 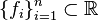 , а
, а  — конечное разбиение
— конечное разбиение  на измеримые множества. Тогда
на измеримые множества. Тогда
 .
.
Определение 3. Пусть теперь  — неотрицательная функция, то есть
— неотрицательная функция, то есть  . Рассмотрим все простые функции
. Рассмотрим все простые функции  , такие что
, такие что  . Обозначим это семейство
. Обозначим это семейство 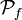 . Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от
. Для каждой функции из этого семейства уже определён интеграл Лебега. Тогда интеграл от  задаётся формулой:
задаётся формулой:

Наконец, если функция  произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:
произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:

где
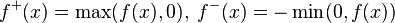 .
.
Определение 4. Пусть  — произвольная измеримая функция. Тогда ее интеграл задаётся формулой:
— произвольная измеримая функция. Тогда ее интеграл задаётся формулой:
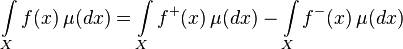 .
.
Определение 5. Пусть наконец  произвольное измеримое множество. Тогда по определению
произвольное измеримое множество. Тогда по определению
 ,
,
где  — индикатор-функция множества
— индикатор-функция множества  .
.
Пример
Рассмотрим функцию Дирихле 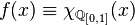 , заданную на
, заданную на  , где
, где  — борелевская σ-алгебра на
— борелевская σ-алгебра на  , а
, а  — мера Лебега. Эта функция принимает значение
— мера Лебега. Эта функция принимает значение 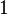 в рациональных точках и
в рациональных точках и  в иррациональных. Легко увидеть, что
в иррациональных. Легко увидеть, что  не интегрируема в смысле Римана. Однако, она является простой функцией на пространстве с конечной мерой, ибо принимает только два значения, а потому её интеграл Лебега определён и равняется:
не интегрируема в смысле Римана. Однако, она является простой функцией на пространстве с конечной мерой, ибо принимает только два значения, а потому её интеграл Лебега определён и равняется:
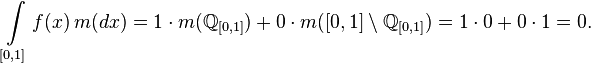
Действительно, мера отрезка 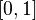 равна 1, и так как множество рациональных чисел счётно, то его мера равна 0, а значит мера иррациональных чисел равна
равна 1, и так как множество рациональных чисел счётно, то его мера равна 0, а значит мера иррациональных чисел равна  .
.




