Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения
Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения частного решения.
Метод состоит в замене произвольных постоянных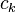 
в общем решении
Соответствующего однородного уравнения
на вспомогательные функции 
, производные которых удовлетворяют линейной алгебраической системе
Определителем системы (1) служит вронскиан функций 
, что обеспечивает её однозначную разрешимость относительно 
.
Если 
— первообразные для , взятые при фиксированных значениях постоянных интегрирования, то функция
Является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.
Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме
Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения частного решения.
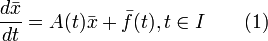
состоит в построении общего решения (1) в виде
где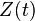 
— базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция 
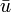, заменившая вектор произвольных постоянных, определена соотношением 
. Искомое частное решение (с нулевыми начальными значениями) при 
имеет вид
Для системы с постоянными коэффициентами последнее выражение упрощается:
Матрица 
называется матрицей Коши оператора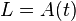 
.
3. Ряд Фурье
Ряд Фурье — представление произвольной функции 
с периодом 
в виде ряда
Этот ряд может быть также записан в виде
где
— амплитуда 
-го гармонического колебания,
— круговая частота гармонического колебания,
— начальная фаза -го колебания,
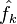— -я комплексная амплитуда
Тригонометрический ряд Фурье
Основная статья: Тригонометрический ряд Фурье
Тригонометрическим рядом Фурье функции 
называют функциональный ряд вида
| (1) |
где
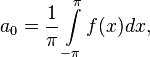
Числа 
, 
и 
(
) называются коэффициентами Фурье функции . Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию 
в виде ряда (1), и нам надо определить неизвестные коэффициенты , и . Если умножить правую часть (1) на 
и проинтегрировать по промежутку 
, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент 
. Аналогично для 
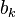
Ряд (1) сходится к функции в пространстве 
. Иными словами, если обозначить через 
частичные суммы ряда (1):
,
то их среднеквадратичное отклонение от функции будет стремиться к нулю:
.
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно.
Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство 
комплекснозначных функций со скалярным произведением
.
Мы также рассматриваем систему функций
.
Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция 
может быть разложена по ним в ряд Фурье:
,
где ряд в правой части сходится к по норме в . Здесь
.
Коэффициенты: 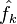связаны с классическими коэффициентами Фурье по следующим формулам:
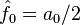
· Комплексная функция вещественной переменной раскладывается в такой же ряд Фурье по мнимым экспонентам, как и вещественная, но, в отличие от последней, для её разложения 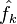и 
не будут, вообще говоря, комплексно сопряженными.
Сходимость ряда Фурье
Сходимость ряда Фурье
