При нагріванні тіл відстані 
між двома точками об’єму А і В змінюється у відповідності з залежністю (1.1):
, (1.1)
де 
– коефіцієнт температурного розширення;
– приріст температури.
Відносна лінійна деформація визначається за формулою:
. (1.2)
При нагріванні куба зі сторонами довжиною 
його об’єм визначається залежністю:
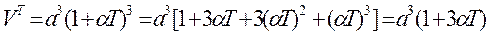. (1.3)
Абсолютна 
і відносна 
зміни об'єму, обумовлені зміною температури
. (1.4)
Якщо відома кількість тепла 
, що вноситься у об'єм, підвищення температури об’єму становить:
, (1.5)
де 
(
) – об’ємна теплоємність.
Відносна зміна об’єму з урахуванням (1.5) визначається формулою:
, 
. (1.6)
Таким чином, при зміні температури у тілі виникають деформації, пропорційні приросту температури (1.2). У загальному випадку при навантаженні і одночасному нагріванні одновимірного об’єкта подовжня деформація складається з трьох складових:
, (1.7)
де 
– пружна деформація;
– пластична деформація;
– температурна деформація.
Поперечна деформація визначається залежністю Пуассона (причому для пластичних деформацій коефіцієнт Пуассона 
):
. (1.8)
Для моделювання процесу утворення температурних напружень необхідно врахувати особливості циклічного деформування матеріалів. Найбільш часто використовуються схеми пружно-пластичного матеріалу (рисунок 1.1) і матеріалу зі зміцненням (рисунок 1.2):
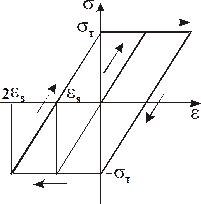
| Рисунок 1.1 – Схема пружно-пластичного матеріалу | Рисунок 1.2 – Схема матеріалу зі зміцненням |
Зважаючи на неоднозначність схематизації пластичного матеріалу зі зміцненням, у більшості випадків у розрахунках використовують простішу діаграму пружно-пластичного матеріалу.
Приклад 1.1 Побудувати діаграму деформування жорстко закріпленого стержня (рисунок 1.3) при нагріванні на 
˚C і охолодженні до початкової температури. При нагріванні довжина стержня намагається збільшитися у відповідності до (1.1), але наявність закріплення призводить до появи деформацій стиску, спочатку пружних, а після досягнення напруженнями у перерізах границі текучості – пластичних (лінія АВ на рисунку 1.4).
Максимальна температурна деформація:
. (1.8а)
| Рисунок 1.3 – Схема жорстко закріпленого стержня | Рисунок 1.4 – Діаграма деформування жорстко закріпленого стержня |
Температура, при якій починаються пластичні деформації (точка А):
, (1.9)
Температура, при якій можуть бути зворотні пластичні деформації (лінія DE):
, (1.9а)
Деформації у стержні у кожний момент задовольняють умові:
, (1.10)
де 
– відповідно, температурна, пружна і пластична деформації.
Після повернення температури до початкової, деформації становлять1:
, 
. (1.11)
Таким чином внаслідок циклічної зміни температури у стержні з’являються пластичні деформації, а у зв’язку з тим, що торці його закріплені жорстко – залишкові розтягуючи напруження, які можуть досягати границі текучості.
Приклад 1.2 Побудувати діаграму деформування для стержня, зображеного на рисунку 1.5.
Рисунок 1.5 – Схема стержня, що закріплений з зазором
При нагріванні стержня сума деформацій не може перевищити величину 
, тобто у даному випадку[2]:
. (1.12)
У процесі нагрівання спочатку вибирається деформація Δ, потім з’являються пружні деформації стиску і відповідні їм напруження
, 
. (1.13)
При подальшому збільшенні температури з’являються пластичні деформації
. (1.14)
При зниженні температури зникають пружні деформації (при цьому Δ=0) і температурні, однак у зв’язку з тим, що торець стержня не закріплений, зниження температури від точки С призведе до переміщення його на величину 
, тобто після завершення температурного циклу у стержні з'являються залишкові деформації . Діаграма деформування представленна на рисунку 1.6.
Рисунок 1.6 – Діаграма деформування стержня,
Що закріплений з зазором
Приклад 1.3 Побудувати діаграму деформування пружно закріпленого стержня (рисунок 1.7) при дії термічного циклу "нагрівання-охолодження". Довжина стержня – l, площа поперечного перерізу А, модуль пружності матеріалу Е, податливість опори δ2 (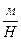
).
Рисунок 1.7 – Схема стержня, закріпленого пружно
На початковому стані нагрівання (ОА) (рисунок 1.8) деформації задовольняють умові:
, (1.15)
де R - реакції опор,
δ - податливість стержня
.
Реакції опар з рівняння (1.15):
. (1.16)
Напруження у поперечних перерізах стержня і поздовжні деформації:
, 
. (1.17)
Наявність пружної опори призводить до зменшення кута φ нахилу до початкової ділянки діаграми, до осі ε і збільшення температури, при якій починаються пластичні деформації (ТS)
, 
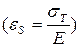. (1.18)
При температурі вищій ТS розвиваються пластичні деформації, а напруження, у відповідності з прийнятою моделлю пружно-пластичного матеріалу, залишаються незмінними (σ =σТ).
Переміщення торця стержня на етапі зростання температури:
. (1.19)
Рисунок 1.8 – Діаграма деформування стержня, що закріплений з зазором
При зниженні температури зменшуються пружні деформації і напруження стиску, і розвиваються пружні деформації і, відповідні їм, напруження розтягу (пряма ВСД). При нагріванні стержня до температури Т>ТВ матимуть місце вторинні пластичні деформації розтягу.
Після завершення термічного циклу, у поперечних перерізах стержня будуть діяти напруження розтягу (σ 
σТ), а торець переміститься на величину Δ (рисунок 1.9).
Рисунок 1.9 – Схема утворення деформацій у стержні,
що закріплений пружно
Умова сумісності переміщень після зниження температури до початкової:
. (1.20)
Звідси знаходимо реакції у закріпленні:
. (1.21)
Пружна деформація стержня:
. (1.22)
Якщо припустити, що температура при нагріванні дорівнювала або перевищувала температуру Тв, пружна деформація досягне максимального значення εпр = εs і скорочення стержня Δ визначатиметься формулою:
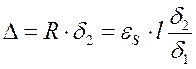. (1.23)
Приклад 1.4 Побудувати діаграму деформування стержня 1, розміщеного у трубі 2, при дії термічного циклу "нагрівання-охолодження" на стержень. Податливості елементів, відповідно, δ1 і δ2 (рисунок 1.10).
Рисунок 1.10 – Схема стержня, розміщеного у трубі
Система є статично-невизначеною і для знаходження реакцій R1 і R2 необхідно використати, крім рівняння рівноваги, рівняння сумісності переміщень:
, (1.24)
де δ1 і δ2 -переміщення, відповідно, торців стержня і труби.
Переміщення δ2 обумовлене дією сили R2, а переміщення δ1 – дією сили R1 і температури Т.
, 
, (1.25)
(Знак "мінус" у першому доданку враховує напрямок сили R1).
Податливості елементів визначаються формулами:
, 
, (1.26)
де А1, А2 – площі поперечного перерізу;
Е1, Е2 – модулі пружності матеріалів.
Розв’язуючи систему рівнянь (1.24), одержимо значення реакцій:
. (1.27)
(Напрямки реакцій вказані на рисунку 1.10).
Напруження у середньому стержні (при σ1 ≤ σТ):
. (1.28)
Як видно з (1.28), при великій жорсткості трубчатого елемента (δ2→0), напруження у стержні 1 такі ж, як і при жорсткому закріпленні (σ1=-αТЕ); при малій (δ2→∞), напруження зменшуються до нульових.
Діаграма деформування повністю аналогічна діаграмі для пружно закріпленого стержня (приклад 1.3) при відносно великій жорсткості трубчатого елемента, тобто тоді, коли у ньому напруження при нагріванні і охолодженні не досягають до границі текучості.
