Шаг 1. Определим внешнюю функцию с помощью команды deffили конструкции function

Шаг 2. Найдем корень уравнения с помощью функции fsolve, подставив в качестве первого параметра заданное начальное приближение.

Шаг 3. Выведем результат, используя команду disp.

Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы найденный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot. Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.

Программа	Результат выполнения
deff('y=F(x)', …'y=sin(x)-cos(x.^2)-sin(2*x)')root=fsolve(1,F)disp(root)x=0.5:0.01:2.5 plot (x,F(x),'-b',root,F(root),'xr',x,0,'-k')	1.1695683

Индивидуальные задания приведены в таблице 3.5

 

Таблица 3.5

Вариант	Уравнение	Начальное приближение
1.
2.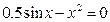
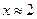
3.
4.
5.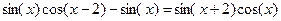
6.
7.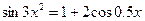
8.
9.
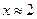
10.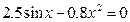
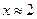
11.
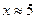
12.
13.
14.
15.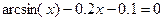

 

Задание 3. Поиск корней полиномиального уравнения, графическая интерпретация

Постановка задачи. Найти все корни полиномиального уравнения. Выполнить графическую интерпретацию для одного из найденных действительных корней.

Шаг 1. Создадим вектор коэффициентов полинома в левой части уравнения (или полином с помощью poly)

Шаг 2. Найдем корни уравнения с помощью функции roots.

Шаг 3. Выведем результат, используя команду disp.

Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы выбранный действительный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot. Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.

Программа	Результат выполнения
v=[2 0 4 -6 -3]R=roots(v)disp(R)root=R(3)x=0.5:0.01:2y=2*x.^4+4*x.^2-6*x-3F_root=2*root^4+4*root^2-6*root-3plot(x,y,'-b',root,F_root,'xr',x,0,'-k')	- 0.4129576 + 1.7282075i - 0.4129576 - 1.7282075i 1.2164706 - 0.3905555

Индивидуальные задания приведены в таблице 3.6.

 

Таблица 3.6

Вариант	Уравнение
1.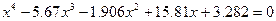
2.
3.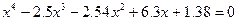
4.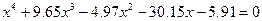
5.
6.
7.
8.
9.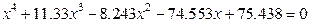
10.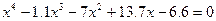
11.
12.
13.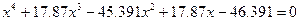
14.
15.

 

Задание 4. Решение системы линейных уравнений

Постановка задачи. Решить систему линейных уравнений.

Шаг 1. Создадим матрицу коэффициентов при неизвестных

Шаг 2. Создадим вектор свободных членов.

Шаг 3. Умножим матрицу, обратную к матрице коэффициентов, на вектор свободных членов (или применим операцию левого матричного деления).

Шаг 4. Выведем результат, используя команду disp.

 

Программа	Результат выполнения
A=[3 1 1;-3 5 6;1 -4 -2]; B=[-4;36;-19]; X=inv(A)*B disp(X)	- 3. 3. 2.

Индивидуальные задания приведены в таблице 3.7.

 

 

Таблица 3.7

№	Система уравнений	№	Система уравнений
1.		2.
3.		4.
5.		6.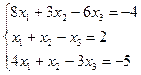
7.		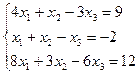8.
9.		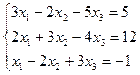10.
11.		12.
13.		14.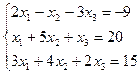
15.		16.