Во время программирования различного рода внешних устройств, регистров процессора, битовыми масками, кодировке цвета, и так далее, приходится работать с кодами беззнаковых целых чисел. При этом использование десятичных чисел крайне неудобно из-за невозможности лёгкого сопоставления числа в десятичном виде и его двоичных бит. А использование чисел в двоичной кодировке крайне громоздко – получаются слишком длинные последовательности нулей и единиц. Программисты используют компромиссное решение – шестнадцатеричную кодировку чисел, где в качестве основания системы счисления выступает число 16. Очевидно, 
. В десятичной системе счисления имеется только 10 цифр: 0,1,2,3,4,5,6,7,8,9. А в 16-ричной системе счисления должно быть 16 цифр. Принято обозначать недостающие цифры заглавными буквами латинского алфавита: A,B,C,D,E,F. То есть
, 
, 
, 
, 
, 
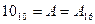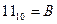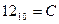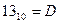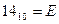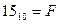. Таким образом, к примеру, 
.
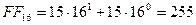В Java для того, чтобы отличать 16-ричные числа, как мы уже знаем, перед ними ставят префикс 0x: 0x FF обозначает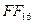 
, а 0x10 – это 1016, то есть 16.
Число N может быть записано с помощью разных систем счисления. Например, в десятичной:
N = An 10n +... + A2 102 + A1 101 + A0 100 (An = 0.. 9)
или в двоичной:
N = Bn 2n +... + B2 22 + B1 21 + B0 20 (Bn = 0 или 1)
или в шестнадцатеричной:
N = Cn 16n +... + C2 162 + C1 161 + C0 160 (Cn = 0.. F)
Преобразование в другую систему счисления сводится к нахождению соответствующих коэффициентов. Например, Bn по известным коэффициентам An – при переводе из десятичной системы в двоичную, или коэффициентов An по коэффициентам Bn - из двоичной системы в десятичную.
Преобразование чисел из системы с меньшим основанием в систему с большим основанием
Рассмотрим преобразование из двоичной системы в десятичную. Запишем число N в виде
N = Bn 2n +... + B2 22 + B1 21 + B0 20 (Bn = 0 или 1)
и будем рассматривать как алгебраическое выражение в десятичной системе. Выполним арифметические действия по правилам десятичной системы. Полученный результат даст десятичное представление числа N.
Пример:
Преобразуем 010111102 к десятичному виду. Имеем:
010111102 = 0×27+1×26+0×25+1×24+1×23+1×22+1×21+0×20=
= 0 + 64 + 0 + 16 + 8 + 4 + 2 + 0 =
= 9410
Преобразование чисел из системы с большим основанием в систему с меньшим основанием
Рассмотрим его на примере преобразования из десятичной системы в двоичную. Нужно для известного числа N10 найти коэффициенты в выражении
N = Bn 2n +... + B2 22 + B1 21 + B0 20 (Bn = 0 или 1)
Воспользуемся следующим алгоритмом: в десятичной системе разделим число N на 2 с остатком. Остаток деления (он не превосходит делителя) даст коэффициент B0 при младшей степени 20. Далее делим на 2 частное, полученное от предыдущего деления. Остаток деления будет следующим коэффициентом B1 двоичной записи N. Повторяя эту процедуру до тех пор, пока частное не станет равным нулю, получим последовательность коэффициентов Bn.
Например, преобразуем 34510 к двоичному виду. Имеем:
частное остаток Bi
345 / 2 172 1 B0
172 / 2 86 0 B1
86 / 2 43 0 B2
43 / 2 21 1 B3
21 / 2 10 1 B4
10 / 2 5 0 B5
5 / 2 2 1 B6
2 / 2 1 0 B7
1 / 2 0 1 B8
34510 = 1010110012
Преобразование чисел в системах счисления с кратными основаниями
Рассмотрим число N в двоичном и шестнадцатеричном представлениях.
N = Bn 2n +... + B2 22 + B1 21 + B0 20 (Bi = 0 или 1)
N = Hn 16n +... + H2 162 + H1 161 + H0 160 (Hi = 0.. F16, где F16 =1510)
Заметим, что 16 = 24. Объединим цифры в двоичной записи числа группами по четыре. Каждая группа из четырех двоичных цифр представляет число от 0 до F16, то есть от 0 до1510. От группы к группе вес цифры изменяется в 24=16 раз (основание 16-ричной системы). Таким образом, перевод чисел из двоичного представления в шестнадцатеричное и обратно осуществляется простой заменой всех групп из четырех двоичных цифр на шестнадцатеричные (по одному на каждую группу) и обратно:
00002 = 016
00012 = 116
00102 = 216
00112 = 316
01002 = 416
01012 = 516
01102 = 616
01112 = 716
10002 = 816
10012 = 916
10102 = A16
10112 = B16
11002 = C16
11012 = D16
11102 = E16
11112 = F16
Например, преобразуем 10110101112 к шестнадцатеричному виду:
10110101112 = 0010 1101 01112 = 2D716
Побитовые маски и сдвиги
| Оператор | Название | Пример | Примечание |
| ~ | Оператор побитового дополнения (побитовое “не”, побитовое отрицание) | ~i | |
| ^ | Оператор “ побитовое исключающее или” (XOR) | i^j | |
| & | Оператор “побитовое и” (AND) | i&j | |
| | | Оператор “побитовое или” (OR) | i|j |
| << | Оператор левого побитового сдвига |
| >>> | Оператор беззнакового правого побитового сдвига |
| >> | Оператор правого побитового сдвига с сохранением знака отрицательного числа |
| &= | y&=x эквивалентно y=y&x |
| |= | y|=x эквивалентно y=y|x |
| ^= | y^=x эквивалентно y=y^x |
| >>= | y>>=x эквивалентно y= y>>x |
| >>>= | y>>>=x эквивалентно y= y>>>x |
| <<= | y<<=x эквивалентно y= y<<x |
Побитовые операции – когда целые числа рассматриваются как наборы бит, где 0 и 1 играют роли логического нуля и логической единицы. При этом все логические операции для двух чисел осуществляются поразрядно – k-тый разряд первого числа с k-тым разрядом второго. Для простоты мы будем рассматривать четырёхбитовые ячейки, хотя реально самая малая по размеру ячейка восьмибитовая и соответствует типу byte.
а) установка в числе a нужных бит в 1 с помощью маски m операцией a|m (арифметический, или, что то же, побитовый оператор OR).
Пусть число a = a3*23 + a2*22 + a1*21 + a0*20, где значения ai – содержание соответствующих бит числа (то есть либо нули, либо единицы).
| a | a3 | a2 | a1 | a0 |
| m | ||||
| a|m | a3 | a1 |
Видно, что независимо от начального значения в числе a в результате нулевой и второй бит установились в единицу. Таким образом, операцию OR с маской можно использовать для установки нужных бит переменной в единицу, если нужные биты маски установлены в единицу, а остальные – нули.
б) установка в числе a нужных бит в 0 с помощью маски m операцией a&m (арифметический, или, что то же, побитовый оператор AND):
| a | a3 | a2 | a1 | a0 |
| m | ||||
| a&m | a2 | a0 |
Видно, что независимо от начального значения в числе a в результате первый и третий бит установились в нуль. Таким образом, операцию AND смаской можно использовать для установки нужных бит переменной в ноль, если нужные биты маски установлены в ноль, а остальные – единицы.
в) инверсия (замена единиц на нули, а нулей на единицы) в битах числа a, стоящих на задаваемых маской m местах, операцией a^m (арифметический, или, что то же, побитовый оператор XOR):
| a | ||||
| m | ||||
| a^m |
Видно, что если в бите, где маска m имеет единицу, у числа a происходит инверсия: если стоит 1, в результате будет 0, а если 0 – в результате будет 1. В остальных битах значение не меняется.
Восстановление первоначального значения после операции XOR – повторное XOR с той же битовой маской:
| a^m | ||||
| m | ||||
| (a^m)^m |
Видно, что содержание ячейки приняло то же значение, что было первоначально в ячейке a. Очевидно, что всегда (a ^ m) ^ m = a, так как повторная инверсия возвращает первоначальные значения в битах числа. Операция XOR часто используется в программировании для инверсии цветов частей экрана с сохранением в памяти только информации о маске. Повторное XOR с той же маской восстанавливает первоначальное изображение. - Имеется команда перевода вывода графики в режим XOR при рисовании, для этого используется команда graphics.setXORMode(цвет).
Ещё одна область, где часто используется эта операция – криптография.
Инверсия всех битов числа осуществляется с помощью побитового отрицания ~a.
Побитовые сдвиги “<<”, “>>” и “>>>” приводят к перемещению всех бит ячейки, к которой применяется оператор, на указанное число бит влево или вправо. Сначала рассмотрим действие операторов на положительные целые числа.
Побитовый сдвиг на n бит влево m<<n эквивалентен быстрому целочисленному умножению числа m на 2n. Младшие биты (находящиеся справа), освобождающиеся после сдвигов, заполняются нулями. Следует учитывать, что старшие биты (находящиеся слева), выходящие за пределы ячейки, теряются, как и при обычном целочисленном переполнении.
Побитовые сдвиги на n бит вправо m>>n или m>>>n эквивалентны быстрому целочисленному делению числа m на 2n. При этом для положительных m разницы между операторами “>>” и “>>>” нет.
Рассмотрим теперь операции побитовых сдвигов для отрицательных чисел m. Поскольку они хранятся в дополнительном коде, их действие нетривиально. Как и раньше, для простоты будем считать, что ячейки четырёхбитовые, хотя на деле побитовые операции проводятся только для ячеек типа int или long, то есть для 32-битных или 64-битных чисел.
Пусть m равно -1. В этом случае m=11112. Оператор m<<1 даст m=111102, но из-за четырёхбитности ячейки старший бит теряется, и мы получаем m=11102=-2. То есть также получается полная эквивалентность умножению m на 2n.
Иная ситуация возникает при побитовых сдвигах вправо. Оператор правого сдвига “>>” для положительных чисел заполняет освободившиеся биты нулями, а для отрицательных – единицами. Легко заметить, что этот оператор эквивалентен быстрому целочисленному делению числа m на 2n как для положительных, так и для отрицательных чисел. Оператор m>>>n, заполняющий нулями освободившиеся после сдвигов биты, переводит отрицательные числа в положительные. Поэтому он не может быть эквивалентен быстрому делению числа на 2n. Но иногда такой оператор бывает нужен для манипуляции с наборами бит, хранящихся в числовой ячейке. Само значение числа в этом случае значения не имеет, а ячейка используется как буфер соответствующего размера.
Например, можно преобразовать последовательность бит, образующее некое целое значение, в число типа float методом Float.intBitsToFloat(целое значение) или типа double методом Double.intBitsToDouble (целое значение). Так, Float.intBitsToFloat(0x7F7FFFFF) даст максимальное значение типа float.
