1. Тело брошено вертикально вверх с начальной скоростью 4м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью вертикально вверх брошено второе тело. На каком расстоянии от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
2. Материальная точка движется прямолинейно с начальной скоростью 10м/с и постоянным ускорением 5м/с2. Определить, во сколько раз путь, пройденный материальной точкой, будет превышать модуль ее перемещения спустя 4с после начала отсчета времени.
3. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью 18км/ч. Далее половину оставшегося времени он ехал со скоростью 22км/ч, после чего до конечного пункта он шел пешком со скоростью 5км/ч. Определить среднюю скорость велосипедиста.
4. Тело брошено под углом 300 к горизонту со скоростью 30 м/с. Каковы будут нормальное и тангенциальное ускорения тела через время 1 с после начала движения?
5. Материальная точка движется по окружности с постоянной угловой скоростью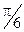 
рад/с. Во сколько раз путь, пройденный точкой за время 4с, будет больше модуля ее перемещения? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол 
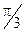рад.
6. Материальная точка движется в плоскости xy согласно уравнениям x=A1+B1t+C1t2 и y=A2+B2t+C2t2, где B1=7м/с, C1=–2м//с2, B2=–1м/с, C2=0,2м/с2. Найти модуль скорости и ускорения точки в момент времени 5с.
7. По краю равномерно вращается с угловой скоростью 1рад/с платформы идет человек и обходит платформу за время 9,9с. Каков наибольшее ускорение a движения человека относительно Земли? Принять радиус платформы 2м.
8. Точка движется по окружности радиусом 30см с постоянным угловым ускорением. Определить тангенциальное ускорение a τ точки, если известно, что за время 4с она совершила три оборота и в конце третьего оборота ее нормальное ускорение a n =2,7 м/с2.
9. При горизонтальном полете со скоростью 250м/с снаряд массой 8кг разорвался на две части. Большая часть массой 6кг получила скорость 400м/с в направлении полета снаряда. Определить модуль и направление скорости меньшей части снаряда.
10. С тележки, свободно движущейся по горизонтали со скоростью 3м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной 4м/с. Определить горизонтальную составляющую скорости u2x человека при прыжке относительно тележки. Масса тележки 210кг, масса человека 70кг.
11. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом 300 к линии горизонта. Определить скорость отката платформы, если снаряд вылетает со скоростью 480м/с. Масса платформы с орудием и снарядами 18т, масса снаряда 60кг.
12. Человек массой 70кг, бегущий со скоростью 9км/ч, догоняет тележку массой 190кг, движущуюся со скоростью 3,6км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
13. Конькобежец, стоя на коньках на льду, бросает камень массой 2,5кг под углом 300 к горизонту со скоростью 10м/с. Какова будет начальная скорость движения конькобежца, если масса его 60кг? Перемещением конькобежца во время броска пренебречь.
14. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его 60кг, масса доски 20кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) 1м/с? Массой колес и трением пренебречь.
15. Снаряд, летевший со скоростью 400м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью 150м/с. Определить скорость большого осколка.
16. Две одинаковые лодки массами 200кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями 1м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами 200кг. Определить скорости u1 и u2 лодок после перебрасывания грузов.
17. На сколько переместится относительно берега лодка длиной 3,5м и массой 200кг, если стоящий на корме человек массой 80кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.
18. Лодка длиной 3м и массой 120кг стоит на спокойной воде. На носу и корме находится два рыбака массами 60кг и 90кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
19. В деревянный шар массой 8кг, подвешенный на нити длиной 1,8м, попадает горизонтально летящая пуля массой 4г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол 30? Размером шара пренебречь. Удар пули считать прямым, центральным.
20. Шар массой 1кг движется со скоростью 4м/с и сталкивается с шаром массой 2кг, движущимися навстречу ему со скоростью 3м/с. Каковы скорости u1 и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
21. Шар массой 3кг движется со скоростью 2м/с и сталкивается с покоящимся шаром массой 5кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
22. Определить КПД неупругого удара бойка массой 0,5т, падающего на сваю массой 120кг. Полезной считать энергию, затраченную на вбивание сваи.
23. Шар массой 4кг движется со скоростью 5м/с и сталкивается с шаром массой 6кг, который движется ему навстречу со скоростью 2м/с. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
24. Из ствола автоматического пистолета вылетела пуля массой 10г со скоростью 300м/с. Затвор пистолета массой 200г прижимается к стволу пружиной, жесткость которой 25кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.
25. Шар массой 5кг движется со скоростью 1м/с и сталкивается с покоящимся шаром массой 2кг. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
26. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью 600м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью 580м/с. С какой скоростью откатилось при этом орудие?
27. Шар массой 2кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
28. Определить работу растяжения двух соединенных последовательно пружин жесткостями 400Н/м и 250Н/м, если первая пружина при этом растянулась на 2см.
29. Из шахты глубиной 600м поднимают клеть массой 3,0т на канате, каждый метр которого имеет массу 1,5кг. Какая работа совершается при поднятии клетки на поверхность Земли? Каков коэффициент полезного действия подъемного устройства?
30. Пружина жесткостью 500Н/м сжата силой 100Н. Определить работу внешней силы, дополнительно сжимающей пружину еще на 2см.
31. Две пружины жесткостью 0,5кН/м и 1кН/м скреплены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации 4см.
32. Какую нужно совершить работу, чтобы пружину жесткостью 800Н/м, сжатую на 6 см, дополнительно сжать на 8см?
33. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на 3мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты 8см?
34. Из пружинного пистолета с пружиной жесткостью 150Н/м был произведен выстрел пулей массой 8г. Определить скорость пули при вылете ее из пистолета, если пружина была сжата на 4 см.
35. Налетев на пружинный буфер, вагон массой 16т, двигавшийся со скоростью 0,6м/с, остановился, сжав пружину на 8см. Найти общую жесткость пружин буфера.
36. Цепь длиной 2м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает 1/3, цепь соскальзывает со стола. Определить скорость цепи в момент ее отрыва от стола.
37. Какая работа должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой 40м, наружным диаметром 3,0м и внутренним диаметром 2,0м? Плотность материала принять равной 2,8·103кг/м3.
38. Шарик массой 60г, привязанный к концу нити длиной 1,2м, вращается с частотой 2с-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния 0,6м. С какой частотой будет при этом вращаться шарик? Какую работу совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
39. По касательной к шкиву маховика в виде диска диаметром 75см и массой 40кг приложена сила 1кН. Определить угловое ускорение и частоту вращения маховика через время 10с после начала действия силы, если радиус шкива равен 12см. Силой трения пренебречь.
40. Диск массой 5кг вращается с частотой 5с-1. Определить работу, которую надо совершить, чтобы частота вращения диска увеличилась до 15с-1. Радиус диска равен 20см.
41. Определить мощность электродвигателя, если его якорь вращается с частотой 25с-1, а момент силы равен 14Н·м.
42. Вычислить, какая энергия выделится, если период вращения Земли увеличится вдвое. Масса Земли 5,98·1024кг радиуса R=6370 км.
43. Горизонтальная платформа массой 120кг вращается с частотой 6 об/мин. Человек массой 80кг стоит на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет в ее центр? Платформу принять за однородный Диск.
44. Диск радиусом R= 30 см и массой m=10 кг вращается с частотой n=5 с-1. Какой момент силы следует приложить, чтобы диск остановился за время t=10с.
45. Тело, имеющее момент инерции l=50 кг·м2, вращается с частотой n=10 с-1. Какой момент силы следует приложить, чтобы частота вращения увеличилась вдвое за время t=20 с?
46. Маховик с моментом инерции 45 кг·м2 начинает вращаться и за время t=5 с его угловая скорость возрастает до 62,8 рад/с. Определить момент силы, действующий на маховик.
47. Однородный стержень массой m =5 кг может свободно вращаться вокруг горизонтальной оси, проходящей через один из его, концов. Вверху угловая скорость стержня ω0=6,28 рад/с. Определить угловую скорость стержня внизу. Длина стержня l=40 см.
48. Снаряд массой m =20 кг имеет вид цилиндра радиусом R=5 см. Снаряд летит со скоростью υ=300 м/с и вращается вокруг оси с частотой n=200 с-1. Вычислить кинетическую энергию снаряда.
49. Маховик с моментом инерции l=60 кг·м2 начинает вращаться под действием момента силы M=120 Н·м. Определить угловую скорость, которую маховик будет иметь через время t=5 с.
50. Молотильный барабан вращается с частотой n =20 с-1. Момент инерции барабана l=30 кг·м2. Определить момент силы, под действием которого барабан остановится за время t=200 с.
51. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой m = 5 кг каждая. Расстояние от каждой гири до оси скамьи l = 70 см. Скамья вращается с частотой n1= 1с-1.Как изменится частота вращения скамьи и какую работу A произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2 = 20 см? Момент инерции человека и скамьи (вместе) относительно оси I= 2,5 кг·м2.
52. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью 4 рад/с. С какой угловой скоростью будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи I=5 кг·м2. Длина стержня l =1,8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
53. Платформа в виде диска диаметром D = 3 м и массой m1=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться эта платформа, если по ее краю пойдет человек массой m2 = 70кг со скоростью 1,8 м/с относительно платформы?
54. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы m1= 280 кг, масса человека m2= 80 кг.
55. На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол 90°? Момент инерции человека и скамьи l равен 2,5 кг·м2, момент инерции колеса l0= 0,5 кг·м2.
56. Однородный стержень длиной l =1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m =7 г, летящая перпендикулярно стержню и его оси. Определить массу M стержня, если в результате попадания пули он отклонится на угол 60°. Принять скорость пули 360 м/с.
57. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n1=8 мин-1, стоит человек массой m1=70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n2=10 мин-1. Определить массу m2 платформы. Момент инерции человека рассчитывать как для материальной точки.
58. На краю неподвижной скамьи Жуковского диаметром D=0,8 м и массой m1=6 кг стоит человек массой m2=60 кг. С какой угловой скоростью ω начнет вращаться скамья, если человек поймает летящий на него мяч массой m=0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r=0,4 м от оси скамьи. Скорость мяча υ=5 м/с.
59. Горизонтальная платформа массой m1=150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n=8 мин-1. Человек массой m2=70 кг стоит при этом на краю платформы. С какой угловой скоростью ω начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека — материальной точкой.
60. Однородный стержень длиной l=1,0 м и массой M=0,7 кг подвешен на горизонтальной оси, проходящей через верхний конец стержня. В точку, отстоящую от оси на 2/3 l, абсолютно упруго ударяет пуля массой m=5 кг, летящая перпендикулярно стержню и его оси. После удара стержень отклонился на угол α=60°. Определить скорость пули.
61. Определить потенциальную и кинетическую энергию массы т = 1 г, совершающей гармоническое колебание с амплитудой А = 1 см и круговой частотой ω = 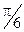сек–1 в моменты t1 =0 и t2=1,5 сек.
62. Длина математического маятника l = 1 м. Масса шарика т = 1 г. Амплитуда колебаний A = 1 см. Определить период колебаний и максимальное значение возвращающей силы. Написать уравнение колебаний шарика, считая начальной фазу, соответствующую его наибольшему отклонению от положения равновесия.
63. Гармонически колеблющаяся материальная точка имеет: амплитуду А= 5см ., массу m = 10 г, полную энергию W = 3,1•10–5 дж. Написать уравнение колебания этой точки. Начальная фаза колебания равна нулю.
64. На стержне длиной l=30 см укреплены два одинаковых грузика: один — в середине стержня, другой — на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период T простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.
65. Точка совершает простые гармонические колебания, уравнение которых x = A sin ωt, где A=5 см, ω = 2 с-1. В момент времени, когда точка обладала потенциальной энергией П=0,1 мДж, на нее действовала возвращающая сила F =5 мН. Найти этот момент времени t.
66. Определить период T простых гармонических колебаний диска радиусом R. = 40 см около горизонтальной оси, проходящей через образующую диска.
67. Определить период T колебаний математического маятника, если его модуль максимального перемещения Δr =18 см и максимальная скорость υmax =16 см/с.
68. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x0 =4 см, а скорость υ0=10 см/с. Определить амплитуду A и начальную фазу φ0 колебаний, если их период Т=2 с.
69. На гладком горизонтальном столе лежит шар массой M=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью R = 500 Н/м. В шар попадает пуля массой m=10 г, летящая со скоростью υ=300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду A и периодT колебаний шара.
70. Шарик массой m=60 г колеблется с периодом T=2 с. В начальный момент времени смещение шарика x0=4,0 см и он обладает энергией E=0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.
71. Интенсивность ультразвука, используемого для лечения заболеваний суставов у крупного рогатого скота, составляет 1,2 104 Вт/м2. Какое количество энергии проходит в тело животного при длительности процедуры 10 мин, если площадь вибратора 12 см2?
72. Количество энергии, передаваемой ультразвуковой волной телу животного при лечении периартрита, за один сеанс должно быть 650 Дж при интенсивности ультразвука 8000 Вт/м2. Сколько времени должен проводиться сеанс, если площадь вибратора 15 см2?
73. Площадь барабанной перепонки человеческого уха 0,65 см2. Вычислить, какая энергия протекает через барабанную перепонку за 1 мин при постоянном шуме в 80 дБ.
74. Шум в помещении птицефабрики днем достигает 95 дБ, а ночью снижается до 65 дБ. Во сколько раз интенсивность звука днем больше, чем ночью?
75. Шум на улице достигает уровня 80 дБ. Такой шум приводит к ухудшению физиологического состояния коров и, в частности, к падению их молочной продуктивности. Во сколько раз надо уменьшить интенсивность шума в коровнике (за счет звукоизоляции) по сравнению с улицей, чтобы уровень шума в нем был не более 60 дБ?
76. На сколько децибел увеличится шум в помещении птицефабрики, если интенсивность звука возрастет: а) в 2000 раз? б) в 20000 раз?
77. Работающая в помещении животноводческого комплекса электродойка создает уровень шума в 75 дБ. Определить уровень шума, когда в помещении будут включены сразу 3 таких установки.
78. Для лечения ряда заболеваний крупного рогатого скота применяется ультразвук с частотой 880 кГц. Показатель поглощения ультразвука этой частоты в мышечных тканях 0,2 см-1. Какова будет интенсивность ультразвука на глубине 5 см, если на поверхности ткани интенсивность его равна 0,6 Вт/м2?
79. Показатель поглощения ультразвука в воде (при частоте 100 кГц) равен 2,5·20-6 см-1. На каком расстоянии от источника интенсивность ультразвука уменьшится вдвое?
80. При прохождении через перегородку из фанеры толщиной 3 мм интенсивность звука снижается в 10 раз. Какова будет интенсивность звука, прошедшего через фанерную, перегородку толщиной 12 мм? Интенсивность звука, падающего на перегородку, равна 10-4 Вт/м2.
81. Определить массу одной молекулы сероуглерода CS2. Принимая, что молекулы в жидкости имеют шарообразную форму и расположены вплотную друг к другу, определить порядок величины диаметра d молекулы.
82. Баллон емкостью V= 50 л заполнен кислородом. Температура кислорода t = 200 C. Когда часть кислорода израсходовали, давление в баллоне понизилось на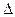 
Р=2атм. Определить массу m израсходованного кислорода.
83. В сосуде объемом V=40 л находиться кислород. Температура кислорода Т=300К. Когда часть кислорода израсходовали, давление в баллоне понизилось на 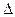p=100 к Па. Определить массу m израсходованного кислорода, если температура газа в баллоне осталась прежней.
84. Баллон емкостью V=15 л содержит смесь водорода и азота при температуре t = 270 C и давление P= 12,3 атм. Масса смеси m=145 г. Определить массу m1 водорода и m2 азота.
85. В баллоне находится газ, при температуре 1500 С. Во сколько раз уменьшится давление газа, если 40% его выйдет из баллона, а температура при этом понизится на 80С?
86. На поверхности Венеры температура и атмосферное давление соответственно равны 750К и 9120 к Па. Найти плотность атмосферы у поверхности планеты, считая, что она состоит из углекислого газа.
87. При сгорании природного газа объемом 1 м2, находящегося при нормальных условиях, выделяется энергия, равная М Дж. Сколько энергии выделяется при сжигании газа объемом 10м3, находящегося под давлением 110 к Па и при температуре 7 0С?
88. В баллоне находится газ, при температуре 1500 С. Во сколько раз уменьшится давление газа, если 40% его выйдет из баллона, а температура при этом понизится на 80С?
89. Найти плотность газовой смеси, состоящей по массе из одной части водорода и 8 частей кислорода при давлении 720мм рт.ст и температуре 150 С.
90. В баллоне находилось 10т газа при давлении 107Па. Какое количество газа взяли из баллона, если окончательное давление стало равно 25 М Па? Температуру газа считать постоянной.
91. В сосуде находится 14 г азота и 9 г водорода при температуре 10 0С и давление 1МПа. Найти массу киломоля смеси и объем сосуда.
92. Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением 10 атм. Считая, что масса кислорода составляет 20% от массы смеси, определить парциальные давления отдельных газов.
93. Некоторый газ находится при температуре 350 К в баллоне емкостью 100л под давлением 2 атм. Теплоемкость этого газа при постоянном объеме Cv = 140 Дж/К. Определить отношение теплоемкостей Ср/Сv .
94. Найти отношение Cp/C v для смеси газов, состоящих из гелия массой 10г и водорода массой 4г.
95. Смесь газов состоит из двух молей одноатомного и трех молей двухатомного газов. Определить молярные теплоемкости Cp и Cv смеси.
96. 6,5г водорода, находящегося при температуре 270С, расширяется вдвое при Р= const за счет притока тепла извне. Найти: 1) работу расширения 2) изменение внутренней энергии газа 3) количество теплоты сообщенного газу.
97. Чему равна энергия твердого движения 20г кислорода при температуре 100С? Какова часть этой энергии приходится на долю поступательного движения и какая часть на долю вращательного?
98. Кинетическая энергия поступательного движения молекул азота, находящихся в баллоне объемом 20 л равна 5 к Дж, а средняя квадратичная скорость его молекул равна 2000 м/с. Найти: 1) количество азота в баллоне 2) давление под которым находится азот.
99. Какое изменение внутренней энергии воздуха массой 290г при его изобарическом нагревании на 200С? Удельная теплоемкость воздуха при постоянном давлении 1000 Дж/кг× К.
100. Удельная теплоемкость при постоянном объеме газовой смеси, состоящей из одного киломоля кислорода и нескольких киломолей аргона, равна 430 Дж/кг град. Какое количество аргона находится в смеси?
101. Найти удельную теплоемкость при постоянном давлении газовой смеси, состоящей из трех киломолей аргона и 2 киломолей азота.
102. Удельная теплоемкость при постоянном объеме газовой смеси, состоящей из 1 киломоля кислорода и нескольких киломолей аргона, равна 430 Дж/ кг К. Какое количество аргона, находится в смеси?
103. 60г кислорода находится под давлением 300 к Па при температуре 100С. После нагревания при постоянном давлении газ занял объем 10л. Найти: 1) количество теплоты, полученного газом 2) энергию теплового движения молекул до и после нагревания.
104. В цилиндр заключено m= 1,6кг кислорода при температуре 300 К и давлении 400кПа. До какой температуры нужно нагреть изобарно кислород, чтобы работа по расширению была равна 40 к Дж?
105. Баллон емкостью 10л содержит азот массой 1г, определить среднюю длину свободного пробега молекулы.
106. Какова длина свободного пробега молекулы гелия при температуре 2000С и давлении 0,01 мм, р т, с т,? Каково число соударений в секунду для одной молекулы?
107. Какова средняя арифметическая скорость(V) молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега молекулы кислорода при этих условиях равна 100 нм.
108. Водород массой 2г занимает объем 2,5л. Определить среднее число столкновений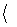 
Z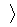 
в единицу времени молекулы водорода.
109. Смесь гелия и аргона находится при температуре Т= 1200К. Определить среднюю квадратичную и кинетическую энергию атомов аргона и гелия.
110. Определить плотность разреженного водорода, если средняя длина свободного пробега молекул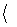 
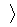= 1 м.
111. Найти зависимость среднего числа столкновений 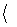Z 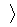молекул идеального газа в 1 с от давления Р при изотермическом процессе: Изобразить эту зависимость на графике.
112. Оценить среднюю длину свободного пробега 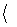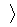и время 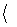t 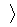между двумя соударениями для 1) молекул водорода при нормальных условиях 2) протонов космических лучей в Галактике. Считать, что средняя плотность межзвездного газа 104 м-3, масса протона практически равна массе атома водорода. Радиус протона r = 10-15 м.
113. Во сколько раз средняя квадратичная скорость пылинки, взвешенной в воздухе, меньше средней квадратичной скорости молекул воздуха? Масса пылинки 10-8г. Воздух считать однородным газом, масса одного киломоля которого равна 29 кг/ моль.
114. Найти среднюю квадратичную и наиболее вероятную скорости молекул водорода. Вычисления выполнить для 3 случаев 1) для температуры Т= 20К, соответствующей температуре кипения водорода 2) для температуры 300К 3) для температуры Т= 5000К, при которой около 95% молекул водорода диссоциированы на атомы.
115. При атмосферном давлении и температуре 00С длина свободного пробега молекулы водорода равна 0,1 мкм. Оцените диаметр этой молекулы.
116. Одинаковые частицы массой m= 10-12 г каждая распределены в однородном гравитационном поле напряженностью G= 0,2 мк Н/кг. Определить отношение n1\n2 концентрации частиц, находящихся на эквипотенциальных уровнях, отстоящих друг от друга на 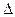Z= 10м. Температура во всех слоях считается одинаковой и равной 290 К.
117. Найти отношение числа молекул водорода N1, скорости которых лежат в пределах от 3000 до 3010 м/с, к числу молекул N2, имеющих скорости в пределах от 1500 до 1510 м/с, если температура водорода 300 К.
118. Какова вероятность того, что данная молекула идеального газа имеет скорость, отличную от 1/2vв не более чем на 1%?
119. Определить относительное число молекул идеального газа, скорости которых заключены в пределах от нуля до 0,01vв.
120. Водород находится при нормальных условиях и занимает объем см3. Определить число молекул в этом объеме, отличающихся скоростями, меньшими некоторого значения V max= 1 м/с.
121. При каком значении скорости V пересекаются кривые распределение Максвелла для температур Т1 и Т2= 2Т1?
122. Вычислить среднее значение скорости V x и среднее значение абсолютной величины V0, компоненты скорости 
V x 
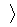молекул в газе, для которого справедливо распределение Максвелла. Масса молекул m= 2,8×10-27 кг, температура Т газа равна = 300 К.
123. Какая часть молекул азота при температуре Т имеет скорость, лежащую в интервале от VВ до VВ+ 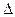V, где 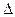V= 20 м/с? Решить задачу для: 1) Т= 400К; 2) Т= 900 К.
124. Масса каждой из пылинок, взвешенных в воздухе, равна 10-18г. Отношение концентрации n1 пылинок на высоте h= 1 м и концентрации n2 их на высоте h0= 0 равно 0,787. температура воздуха 300 К. Найти по этим данным значение постоянной Авогадро NА.
125. Определить массу газа m, заключенного в вертикальном цилиндрическом сосуде, площадь основания S и высота h. Давление газа на уровне нижнего основания цилиндра Р, молярной массы газа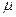 
. Считать, что Т и g не зависят от высоты.
126. Какая часть молекул газа имеет кинетическую энергию, достаточную для преодоления гравитационного поля Земли, если температура газа 300К? Расчеты провести для молекул: а) водорода; б) азота.
127. В сосуде находится 8 г кислорода при температуре 1600 К. Какое число молекул кислорода имеет кинетическую энергию поступательного движения, превышающее значение W= 6,65 10-20 Дж?
128. Найти коэффициент диффузии гелия при нормальных условиях.
129. При каком давлении отношение коэффициента внутреннего трения некоторого газа коэффициенту его диффузии равно 0,3 кг/м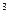 
? Средняя квадратичная скорость его молекул равна 632 м/с.
130. Найти среднюю длину свободного пробега молекул гелия при температуре 0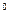 
С и давлении 100 кПа, если при этих условиях коэффициент внутреннего трения (динамическая вязкость) для него равен 1,310×10 
г/см×с.
131. Найти диаметр молекулы кислорода, если известно, что для кислорода коэффициент внутреннего трения при 0 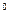С равен 18,8×10 
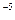Н×с/м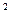 
.
132. Коэффициенты диффузии и внутреннего трения водорода при некоторых условиях равны соответственно D=1,42 см 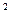/с и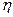 
= 8,5×10 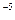Н×с/м. Найти число молекул водорода в 1 м .
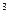133. Найти коэффициент теплопроводности воздуха при температуре 10 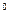С и давлении 10 
Н/см 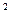. Диаметр молекулы воздуха принять равным 3×10 
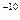м.
134. В сосуде объемом 2 литра находится 4×10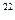 
молекул двухатомного газа. Коэффициент теплопроводности газа равен 0,014 Вт/м×К. Найти коэффициент диффузии газа при этих условиях.
135. Углекислый газ и азот находится при одинаковых температурах и давлении. Найти для этих газов отношение: 1) коэффициентов диффузии; 2) коэффициентов внутреннего трения; 3) коэффициентов теплопроводности. Диаметр молекул этих газов считать одинаковым.
136. Коэффициент диффузии кислорода при температуре 0 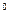С равен 0,19 см 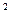/с. Определить среднюю длину свободного пробега молекул кислорода.
137. Вычислить коэффициент диффузии азота при давлении 100 Па и температуре 300К.
138. В сосуде вместимостью 10л находится азот массой 0,25 кг. Определить: 1) внутреннее давление газа; 2) собственный объем молекул.
139. Определить давление, которое будет производить кислород в количестве 1 моля, если он занимает объем 0,5 л, при температуре 300К. Сравнить полученный результат с давлением, вычисленным по уравнению Клапейрона-Менделеева.
140. Какую температуру имеют 2г азота, занимающего объем 820 см3, при давлении 200 кПа? Газ рассматривать как: 1)идеальный; 2) реальный.
141. Один киломоль кислорода находится при температуре 27 0С и давлении 100кПа. Найти объем газа, считая, что кислород при данных условиях ведет себя как реальный газ.
142. Найти эффективный диаметр молекулы кислорода, считая, что практические величины Tк и pк для кислорода составляют соответственно 154К и 5МПа. Найти среднюю длину свободного пробега молекул углекислого газа при нормальных условиях. Эффективный диаметр молекулы вычислить, считая для углекислого газа Тк =304 К и давление рк=7,3 МПа.
143. В сосуде объемом 10 л находится 0,25 кг азота при температуре 27 0С: 1) какую часть давления газа составляет давление, обусловленное силами взаимодействия молекул? 2) какую часть объема сосуда составляет собственный объем молекул?
144. Определить наибольший объем, который может занимать вода, содержащая количество вещества 1 моль.
145. Найти внутреннюю энергию углекислого газа массой 132г при нормальном давлении и температуре 300К в двух случаях, когда газ рассматривают: 1) как идеальный; 2) как реальный.
146. При изотермическом расширении водорода массой 1г объем газа увеличился в два раза. Определить работу расширения, совершенную газом, если температура газа 15 0С. Определить теплоту, переданную газам при этом.
147. В цилиндре под поршнем находится водород массой 20г при температуре 20 0С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и полную работу, совершенную газом.
148. Кислород массой 200 г занимает объем 100л и находится под давлением 200кПа. При нагревании газ расширился при постоянном давлении до объема 300л, а затем его давление возросло до 500кПа при неизменном объеме. Найти изменение внутренней энергии газа, совершенную газом работу и теплоту, переданную газу.
149. Из баллона, содержащего водород под давлением 10 атм. при температуре 180С, выпустили половину содержащегося в нем количества газа. Считая процесс адиабатическим, определить конечную температуру и давление.
150. При адиабатическом сжатии давление воздуха было увеличено от 50кПа до 0,5МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление газа в конце процесса.
151. Какая доля количества теплоты, подводимого к идеальному двухатомному газу при изобарном процессе, расходуется на увеличение внутренней энергии газа и какая доля на работу расширения? Рассмотреть 3 случая: 1) одноатомный; 2) двухатомный; 3) трехатомный.
152. Определить работу изотермического сжатия газа, совершающего цикл Карно, КПД которого 0,4, если работа изотермического расширения равна 8Дж.
153. Найти изменение энтропии при превращении 10г льда при –20 0С в пар при 100 0С.
154. Водород массой 6,6г расширяется изобарически до удвоения объема. Найти изменение энтропии при этом расширении.
155. Смешали воду массой m1=5кг при температуре Т1=280К с водой массой m2=8кг при температуреТ2=350К. Найти изменение энтропии, происходящее при смешивании.
156. Какое количество теплоты выделится, если азот массой m=1г, взятый при температуре Т=280К под давлением р1=0,1 МПа изотермически сжать до давления р2=1МПа?
157. Кислород массой 2кг увеличил свой объем в пять раз, один раз изотермически, другой – адиабатически. Найти изменения энтропии в каждом из указанных случаев.
158. В цилиндре под поршнем находится кислород массой 0,016 кг при температуре Т1=300К. Газ сначала расширился адиабатически, увеличив свой объем в пять раз, а затем был сжат изотермически, причем его объем уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и полную работу, совершенную газом.
159. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление газа в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего. Определить термический КПД цикла.
160. Какая доля количества теплоты, подводимого к трех атомному идеальному газу, расходуется на увеличение внутренней энергии газа, а какая - на работу по расширению?
161. Четыре положительных заряда по 10-7 Кл каждый помещены в вершинах квадрата. Какой отрицательный заряд надо поместить в центр квадрата, чтобы вся система находилась в равновесии? Будет ли это равновесие устойчивым?
162. С какой силой взаимодействуют длинная проволока с линейной плотностью заряда 10-8 Кл/м и точечный заряд 2∙10-8 Кл, находящийся на расстоянии 3 см от проволоки, близко к ее середине? (Задачу решить, используя закон Кулона.)
163. Два шарика с массами 0,1 кг подвешены в одной точке на нитях длиной 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол 60 0. Найти заряд каждого шарика.
164. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на некоторый угол. Шарики погрузили в масло, плотность которого равна 8∙10 2 кг/м3. Какова диэлектрическая проницаемость масла, если угол расхождения нитей при погружении шариков в масло остается неизменным? Плотность материала шариков 1,6∙10 3 кг/м3.
165. Два положительных точечных заряда 1q и 4q закреплены на расстоянии 60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии.
166. Тонкий стержень длиной 10 см равномерно заряжен. Линейная плотность заряда 2∙10-6 Кл/м. На продолжении оси стержня на расстоянии 20 см от ближайшего его конца находится точечный заряд 1∙10 –7 Кл. Определить силу взаимодействия стержня и точечного заряда.
167. Тонкий длинный стержень равномерно заряжен с линейной плотностью заряда 1∙10 –5 Кл/м. На перпендикуляре к оси стержня на расстоянии 20 см от его конца находится точечный заряд 1∙10-8 Кл. Расстояние заряда до конца стержня 20 см. Найти силу взаимодействия заряженного стержня и точечного заряда.
168. Тонкое кольцо радиусом 10 см несет равномерно распределенный заряд 0,1∙10 –6 Кл. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд 1∙10 –8 Кл. Определить силу, действующую на точечный заряд со стороны заряженного кольца, если он удален от центра кольца на 20 см.
169. Электрон, двигавшийся со скоростью 5∙10 6 м/с, влетает в параллельное его движению электрическое поле напряженностью 1∙10 3 В/м. Сколько времени будет двигаться электрон до момента остановки?
170. Пылинка взвешена в плоском конденсаторе. Ее масса 10 –11 г, расстояние между пластинами конденсатора 0,5 см. Пылинка освещается ультрафиолетовым светом и, теряя заряд, выходит из равновесия. Какой заряд потеряла пылинка, если первоначально к конденсатору было приложено напряжение 154 В, а затем, чтобы опять вернуть пылинку в равновесие, пришлось прибавить 8 В?
171. Между вертикальными пластинами плоского конденсатора, находящегося в воздухе, подвешен на тонкой шелковой нити маленький шарик, несущий заряд 3,3∙10 –9 Кл. Какой величины заряд надо сообщить пластинам конденсатора, чтобы нить с шариком отклонилась на угол 75 0 от вертикали? Масса шарика 0,04 г, площадь пластин конденсатора 314 см2. Массой нити можно пренебречь.
172. Конденсатор состоит из трех полосок станиоли площадью по 6 см2 каждая, разделенных двумя слоями слюды толщиной 0,1 мм. Крайние полоски станиоли соединены между собой. Какова емкость такого конденсатора? Диэлектрическая проницаемость слюды равна 7.
173. Три конденсатора с емкостями 1 мкФ, 2 мкФ и 3 мкФ, имеющие максимально допустимые напряжения соответственно 1000 В, и 500 В соединены в батарею. При каком соединении конденсаторов можно получить наибольшее напряжение? Чему равны напряжение и емкость батареи?
174. Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов 150 В. Определить разность потенциалов на конденсаторах, если после отключения их от источника тока у одного конденсатора уменьшили расстояние между пластинами в два раза.
175. Конденсатор, заряженный до напряжения 100 В, соединяется с конденсатором такой же емкости, но заряженным до 200 В: один раз одноименно заряженными обкладками, другой – разноименно заряженными обкладками. Какое напряжение установится между обкладками в обоих случаях?
176. Заряженная частица, пройдя ускоряющую разность потенциалов 600кВ, приобрела скорость 5,4∙10 6 м / с. Определить удельный заряд частицы / отношение заряда к массе /.
177. Электрон с начальной скоростью 3∙10 6 м/с влетел в однородное электрическое поле напряженностью 150 В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Найти скорость электрона через 0,1∙10 –3 с.
178. Плоский воздушный конденсатор состоит из двух пластин, расположенных на расстоянии 4 мм друг от друга, общей площадью 100 см2 Конденсатор заряжают от батареи в 200 В и отключают от нее. Какую работу надо совершить, чтобы увеличить расстояние между обкладками в два раза?
179. На сколько изменится энергия плоского воздушного конденсатора, если параллельно его обкладкам ввести металлическую пластину толщиной 1 мм. Площадь обкладок конденсатора и пластины 150 см2, расстояние между обкладками 6 мм. Конденсатор заряжен 400 В и отключен от батареи.
180. Определить ускоряющую разность потенциалов, которую должен пройти электрон в электрическом поле, обладающий скоростью 10 6 м/с, чтобы скорость его возросла в два раза.
181. Какую работу необходимо совершить, чтобы перенести точечный заряд 2х 10 –8 Кл из бесконечности в точку, находящуюся на расстоянии 28 см от поверхности проводящего шара радиусом 2 см, если потенциал шара равен 300 В? Шар находится в воздухе.
182. Сила тока в проводнике равномерно возрастает нарастает от 0 до 2 А в течение времени 5 с. Определите заряд, прошедший по проводнику.
183. Обмотка катушки из медной проволоки при температуре 14 0С имеет сопротивление обмотки 10 Ом. После пропускания тока сопротивление обмотки стало равно 12,2 Ом. До какой температуры нагрелась обмотка?
184. В схеме ε 1=2,1 В, ε 2=1,9 В, R1=45 Ом, R2=10 Ом, R3=10 Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь.
185. 
Определить силу токов на всех участках электрической (рис 1), если ε1=10 В, ε2=12 В, R1=2 Ом, R2=2 Ом, R3 =8 Ом, R4=4 Ом.
186.
 |
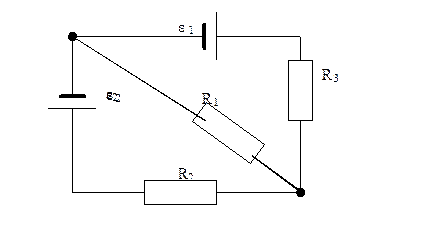Два источника тока ε1=10 В с внутренним сопротивлением r1=2 Ом и ε2=6В с внутренним сопротивлением r2=2 Ом соединены, как показано на рисунке. Определить силы тока в проводнике и источниках тока. Сопротивление проводника R=6 Ом.
187. Два источника тока, ЭДС которых 1,6 В и 2 В, а внутренние сопротивления 0,3 и 0,2 Ом соответственно, соединены последовательно и дают во внешнюю цепь силу тока 0,4 А. Определить сопротивление внешней цепи.
188. Амперметр с сопротивлением 0,02 А рассчитан на измерение силы тока 1 А. Каким должно быть сопротивление шунта, чтобы этим прибором можно было измерить ток силой до 10 А.
189. Источник с Э.Д.С. 2 В имеет внутреннее сопротивление 0,5 Ом. Определите падение напряжения внутри источника при токе в цепи 0,25 А. Найдите внешнее сопротивление цепи при этих условиях.
190. Электродвижущая сила элемента и его внутренне сопротивление равны соответственно 1,6 В и 0,5 Ом. Чему равен КПД элемента при токе 2,4 А?
191. Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим – 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
192. ЭДС батареи 80 В, внутреннее сопротивление 5 Ом. Внешняя цепь потребляет мощность 100 Вт. Определить силу тока в цепи, напряжение, под которым находится внешняя цепь, и ее сопротивление.
193. ЭДС батареи 12 В. При силе тока 4 А КПД батареи 0,6. определить внутреннее сопротивление батареи.
194. Сила тока в проводнике меняется со временем по закону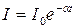 
. Начальная сила тока 20 А, α=102 с-1. Определить теплоту, выделившуюся за это время в проводнике.
195. Прибор с сопротивлением 6 Ом подключен к двум параллельно соединенным источникам тока с ЭДС 2,2 В и 2,4 В и внутренним сопротивлением 0,8 Ом и 0,2 Ом. Определить силу тока в этом приборе и напряжение на зажимах второго источника тока.
196. При электролизе раствора серной кислоты расходуется мощность 37 Вт. Определите сопротивление электролита, если за 500 мин выделяется 0,3 г водорода.
197. При электролизе медного купороса за один час выделилось 0,5 г меди. Площадь каждого электрода равна 75 см2. Найти плотность тока.
198. Рентгеновские лучи ионизируют воздух так, что в 1 см2 ежесекундно образуется 109 пар ионов. Коэффициент рекомбинации 10-5 см3/с. Заряд иона равен заряду электрона. Какую удельную электропроводность имеет ионизированный воздух при равновесии?
199. В медном проводе длиной 2 м и площадью поперечного сечения 0,4 мм2 идет ток. При этом в каждую секунду выделяется теплота 0,35 Дж. Сколько электронов проходит через поперечное сечение проводника за время 1 с?
200. Два длинных параллельных провода находятся на расстоянии 5см один от другого. По проводам текут в противоположных направлениях одинаковые токи 10 А каждый. Найти напряженность магнитного поля в точке, находящейся на расстоянии 2 см от одного и 3 см от другого провода.
201. Бесконечно длинный прямой провод согнут под прямым углом. По проводу течет ток 100 А. Вычислить магнитную индукцию в точках, лежащих на биссектрисе угла и удаленных от вершины угла на 10 см.
202. По двум параллельным проводам длиной 1м каждый текут одинаковые токи. Расстояние между проводами равно 2 см. Токи взаимодействуют с силой 1 мН. Найти силу тока в проводах.
203. Индукция магнитного поля в точке, лежащей на оси проводящего кольца на расстоянии 0,6 м от плоскости кольца, равна 50 мТл. Определить силу тока в кольце. Радиус кольца 0,8 м.
204. Электрон движется в магнитном поле с индукцией 0,02 Тл по окружности радиусом 1 см. Определить кинетическую энергию электрона.
205. Заряженная частица, обладающая скоростью 2∙106 м/с влетела в однородное магнитное поле с индукцией 0,52 Тл.∙ Найти отношение заряда частицы к ее массе, если частица в поле описала дугу окружности радиусом 4 см.
206. Электрон движется в однородном магнитном поле напряженностью 4 кА/м со скоростью 10 Мм/с. Вектор скорости направлен перпендикулярно линиям напряженности. Найти силу, с которой поле действует на электрон.
207. В однородное магнитное поле с индукцией 0,2 Тл находится проволочное кольцо радиуса 1 см. Магнитные силовые линии перпендикулярны плоскости кольца. Определить ЭДС индукции, возникающую в кольце, если магнитное поле равномерно уменьшается до нуля за время 0,01 с.
208. В однородном магнитном поле с индукцией 3 Тл перемещается перпендикулярно силовым линиям прямолинейный проводник длиной 15 см со скоростью 10 м/с. Какая разность потенциалов возникает на концах проводника.
209. Соленоид длиной 10 см и сопротивлением 30 Ом содержит 200 витков. Определить индукцию магнитного поля соленоида, если разность потенциалов на концах обмотки 6 В.
210. Соленоид сопротивлением 6 Ом имеет 1000 витков. Напряжение на концах обмотки 12 В. Найти длину соленоида, если индукция его магнитного поля 3,78 мТл.
211. Соленоид намотан из проволоки сопротивлением 32 Ом При напряжении на концах проволоки 3,2 В индукция внутри соленоида 628 мкТл. Определить число витков соленоида на 1м длины.
212. Как изменится сила, действующая на проводник с током в однородном магнитном поле, если угол между направлениями поля и тока изменится с 30° до 60°?
213. На каком расстоянии друг от друга надо расположить два длинных параллельных проводника с током силой 1 А, чтобы он взаимодействовали с силой 1,6 мкН на каждый метр длины?
214. По двум параллельным длинным проводникам текут токи одинаковой силы. Как изменится сила взаимодействия проводников, приходящаяся на единицу длины, если расстояние между проводниками изменится с 80 см до 20см?
215. Два длинных проводника расположены параллельно на расстоянии 20 см друг от друга. По проводникам текут токи 10 А и 5 А. Определить силу взаимодействия проводников, приходящуюся на каждый метр длины
216. По двум длинным параллельным проводникам текут токи 5 А и 3 А. Расстояние между проводниками 10 см. Определить силу взаимодействия, приходящуюся на 1 м длины проводов, Как изменится эта сила, если проводники раздвинуть на расстояние 30 см?
217. Очень короткая катушка содержит 600 витков тонкого провода. Катушка имеет квадратное сечение со стороной 8 см. Найти магнитный момент катушки при силе тока 1 А.
218. Протон движется по окружности радиусом 1 мм в однородном магнитном поле с индукцией 0,2 Тл. Какова кинетическая энергия протона?
219. Электрон, пройдя ускоряющую разность потенциалов 1 кВ, влетел в однородное магнитное поле с индукцией 2 мТл под углом 45°. Определить силу, действующую на электрон.
220. Протон влетел в однородное магнитное поле, индукция которого 20 мТл, перпендикулярно силовым линиям поля и описал дугу радиусом 5 см. Определить импульс протона.
221. Электрон влетел в однородное магнитное поле, индукция которого 200мкТл, перпендикулярно силовым линиям и описал дугу окружности радиусом 4 см. Определить кинетическую энергию электрона.
222. Проводник длиной 1 м движется со скоростью 5 м/с перпендикулярно линиям индукции однородного магнитного поля. Определить магнитную индукцию, если на концах проводника возникает разность потенциалов 0,02 В.
223. Протон, пройдя ускоряющую разность потенциалов 600 В, движется параллельно длинному прямому проводу на расстоянии 2 мм от него. Какая сила действует на протон, если по проводу идет ток 10 А?
224. Электрон, пройдя ускоряющую разность потенциалов 1кВ, влетел в однородное магнитное поле под углом 30°. Определить индукцию магнитного поля, если оно действует на электрон с силой 3∙10 -18Н.
225. В соленоиде объемом 500 см3 с плотностью обмотки 104 витков на метр при увеличении силы тока наблюдалась э. д. с. самоиндукции 1 В. Каковы скорость изменения силы тока и магнитного потока в соленоиде? Сердечник соленоида немагнитный.
226. Магнитный поток 10-2 Вб пронизывает замкнутый контур. Определить среднее значение э. д. с. индукции, которая возникает в контуре, если магнитный поток изменится до нуля за время 0,001 с.
227. Определить магнитный поток в соленоиде длиной 20 см, сечением 1см2, содержащем 500 витков при токе силой 2 А. Сердечник немагнитный.
228. В однородном магнитном поле с индукцией 0,2 Тл равномерно с частотой 10 с-1 вращается рамка, площадь которой 100 см2. Определить мгновенное значение э.д.с, соответствующее углу 450 между плоскостью рамки и силовыми линиями поля.
229. Плоский контур с током 5 А свободно установился в однородном магнитном поле с индукцией 0,4 Тл. Площадь контура 200 см2. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол 400. Определить совершенную при этом работу.
230. Квадратная проволочная рамка со стороной 5 см и сопротивлением 10 мОм находится в однородном магнитном поле с индукцией 40 мТл. Нормаль к плоскости рамки составляет угол 300 с линиями магнитной индукции. Определить заряд, который пройдет по рамке, если магнитное поле выключить.
231. В катушке при изменении силы тока от 0 до 2 А за время 0,1с возникает э. д. с. самоиндукции 6 В. Определить индуктивность катушки.
232. Индуктивность катушки 10,5 Гн. Определить э. д. с. самоиндукции, если за время 0,1 с сила тока в катушке, равномерно изменяясь, уменьшилась с 25 А до 20 А.
233. Плоский конденсатор с площадью пластин 100 см2, разделенных слоем парафинированной бумаги толщиной 0,01 мм, и катушка образуют колебательный контур. Частота колебаний в контуре 1 кГц. Какова индуктивность катушки контура?
234. Индуктивность соленоида, намотанного в один слой на немагнитный каркас, равна 0,5 мГн. Длина соленоида равна 0,6 м, диаметр 2 см. определить отношение числа витков соленоида к его длине.
235. Колебательный контур, состоящий из воздушного конденсатора с площадью пластин 50 см2 каждая и катушки с индуктивностью 1 мкГн, резонирует на длину волны 20 м. Определить расстояние между пластинами конденсатора.
236. Конденсатор емкостью 1 пФ соединен параллельно с катушкой длиной 20 см и сечением 0,5 см2, содержащей 1000 витков. Сердечник немагнитный. Определить период колебаний
237. Колебательный контур состоит из катушки индуктивностью 1 мГн и конденсатора переменной емкости. При какой емкости контур резонирует с колебаниями, имеющими частоту 10 кГц?
238. Плоский конденсатор с площадью пластин 100 см2 и стеклянным диэлектриком толщиной 1 мм соединен с катушкой самоиндукции длиной 20 см и радиусом 3 см, содержащей 1000 витков. Определить период колебаний в этой цепи.
239. Колебательный контур состоит из катушки индуктивности 0,01 Гн и конденсатора емкостью 1 мкф. Определить частоту колебаний в контуре.
240. Колебательный контур состоит из плоского конденсатора с площадью пластин 50 см2, разделенных слюдой толщиной 0,1 мм, и катушки индуктивностью 10-3 Гн. Определить период колебаний в контуре.
241. Вычислить увеличение лупы с фокусным расстоянием f =3 см.
242. Полученное с помощью линзы изображение предмета на экране в пять раз больше предмета. Расстояние между предметом и экраном l = 150 см. Определить оптическую силу линзы и ее фокусное расстояние.
243. Какое увеличение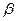 
дает линза с оптической силой D = 5 дптр, если она находится на расстоянии a = 25 см от предмета?
244. Увеличение микроскопа 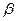=600. Определить оптическую силу D1 объектива, если фокусное расстояние окуляра f2 = 4 см, а длина тубуса L = 24см.
245. Фокусные расстояния объектива и окуляра соответственно равны f1=3 мм, f2 = 3 см. Предмет находится на расстоянии s = 3,1 мм от объектива. Вычислить увеличение объектива и окуляра микроскопа.
246. Человек с нормальным зрением пользуется линзой с оптической силой D = 16 дптр как лупой. Какое увеличение дает такая лупа?
247. Фокусное расстояние объектива микроскопа f1 = 4 мм, окуляра f2 =5 см. Найти увеличение этого микроскопа, если предмет помещен на расстоянии s = 4,2 мм от объектива микроскопа.
248. Оптическая сила объектива D=2,1 дптр. Расстояние от объектива до экрана s1 = 10 м. Каково увеличение объектива?
249. Определить диаметр изображения среза мышечного волокна диаметром 9 см, рассматриваемого под микроскопом с фокусным расстоянием окуляра f1 = 14 см и объектива f2 = 0,2 см. Расстояние между фокусами объектива и окуляра 20 см.
250. Определить оптическую силу объектива, дающего десятикратное увеличение. Расстояние от объектива до экрана s1 =3,7 м.
251. Норма минимальной освещенности содержания животных Е=20 лк (лампы накаливания). Определить силу света лампы, подвешенной на высоте 3 м. Расчет произвести при условии, что эту освещенность создают две лампы, расположенные на расстоянии 8 м друг от друга.
252. На рабочем месте приготовления кормов следует создать освещенность Е=100 лк. На какой высоте должна быть подвешена лампа силой света I=100 кд?
253. Норма минимальной освещенности для содержания птиц Е=20 лк (лампы накаливания). Определить силу света лампочки, подвешенной на высоте 1 м при угле падения света 600.
254. На каком расстоянии друг от друга необходимо подвесить две лампы в теплицах, чтобы освещенность на поверхности Земли в точке, лежащей посередине между лампами, была не менее 200 лк? Сила света каждой лампы 800 кд.
255. Светильник имеет форму шара с диаметром 20 см. Полный световой поток, равномерно испускаемый шаром во все стороны, равен 2512 лм. Найти силу света, светимость и яркость шара.
256. Лист бумаги освещается светом, рассеянным от экрана площадью 500 см2 в направлении нормали к экрану. Светимость экрана составляет 100 лм/ м2. Лист бумаги расположен на расстоянии 2 м от экрана и образует с ним угол 300. Определить освещенность листа бумаги.
257. Над центром круглого стола радиусом 1 м подвешен светильник в виде плоского горизонтального диска площадью 100 см2. Яркость светильника не зависит от направления и равна В= 1,6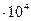 
кд/м2. На какой высоте от поверхности стола надо поместить светильник, чтобы освещенность периферийных точек стола была максимальной? Какова будет эта освещенность?
258. Светильник в виде равномерно светящегося шара радиусом r= 10 см имеет силу света I = 100 Кд. Определите для этого светильника: 1) полный световой поток Ф0; 2) светимость R.
259. Отверстие в корпусе фонаря закрыто идеально матовым стеклом (т.е. яркость источника не зависит от направления) размером 7,5х10 см. Сила света I фонаря в направлении, составляющем угол 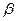= 300,равна 12 кд. Определите яркость В стекла.
260. На лист белой бумаги размером 10х25 см нормально к поверхности падает световой поток Ф=50 лм. Принимая коэффициент рассеяния бумажного листа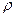 
= 0,7, определите для него: 1) освещенность; 2) светимость; 3) яркость.
261. В опыте с бипризмой Френеля расстояние между мнимыми источниками света d =0,5 мм, длина волны монохроматического света, падающего на бипризму, = 500 нм. Расстояние между интерференционными максимумами на экране 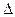x= 1,5 мм. Определить расстояние l от мнимых источников до экрана.
262. На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза с радиусом кривизны R =6 м
