Цель работы: познакомиться с приемами решения задач линейной алгебры.
Типичными задачами линейной алгебры являются задачи, связанные с решением систем линейных уравнений. При этом приходится работать с массивами чисел. Для их обработки в Excel предусмотрен ряд математических функций:
· МОПРЕД(массив) - функция для нахождения определителя квадратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
· МОБР(массив) - функция для нахождения обратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
· МУМНОЖ(массив1;массив2) - функция для нахождения произведения массива1 на массив2. Результатом является массив с таким же числом строк, как массив1, и с таким же числом столбцов, как массив2. При этом если обозначить буквой С результат произведения двух массивов А и В, то элементы массива С определяются по формуле  , где i — номер строки, а j — номер столбца;
, где i — номер строки, а j — номер столбца;
· ТРАНСП(массив) - функция для транспонирования массива ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и т.д.
Особенностью вычислений, связанных с массивами, является то, что результат вычисления распространяется в виде формулы на целый блок ячеек. Такие формулы называются формулами массива. При вводе формул массива необходимо соблюдать определенную последовательность действий:
Шаг 1. Сначала формула вводится в первую ячейку результирующего массива.
Шаг 2. Выделяется весь блок ячеек результирующего массива.
Шаг 3. Нажимается клавиша <F2> клавиатуры.
Шаг 4. Нажимается комбинация клавиш Ctrl+Shift+Enter. При этом формула распознается как формула массива и заключается в фигурные скобки { }.
Важно!
При работе с массивами чисел всегда контролируйте размерность результирующего массива!
ЗАДАНИЕ 1. Решение задач линейной алгебры
Рассмотрим решение некоторых задач линейной алгебры на простейших примерах. Пусть дана квадратная матрица 3-го порядка 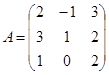 .
.
· Найдите матрицу А-1, обратную к данной матрице А.
· Найдите определитель матрицы А.
· Проверьте, что найденная матрица А-1 действительно является обратной для матрицы А.
1. Откройте чистый рабочий лист. Переименуйте его в Обратная матрица.
2. Заполните рабочий лист исходными данными, как показано на рис. 14:
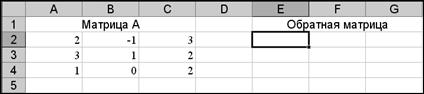
Рис. 14
3. Установите курсор в ячейку Е2 и введите формулу =МОБР(А2:С4). После нажатия клавиши Enter в ячейке Е2 появится число 0,4.
4. Для получения обратной матрицы формулу в этом примере необходимо ввести как формулу массива. Для этого выделите диапазон ячеек Е2:G4, соответствующий обратной матрице (размерность матрицы А-1 очевидно будет такая же, как и у матрицы А). Нажмите клавишу <F2>, а затем комбинацию клавиш Ctrl+Shift+Enter. В результате ячейки Е2:G4 будут заполнены элементами обратной матрицы.
5. В ячейку А6 введите текст Определитель(A).
6. Установите курсор в ячейку В6 и введите формулу = МОПРЕД(А2:С4). Нажмите клавишу Enter. В ячейке должно получиться значение определителя матрицы А, равное 5. Внимание! В этом случае формулу для расчета определителя не нужно вводить как формулу массива, так как определитель является не массивом, а одним числом.
7. Для проверки правильности нахождения обратной матрицы вспомним, что должно выполняться условие: А А-1=Е, где Е - единичная матрица того же порядка, что и матрица А. Установите курсор в ячейку Е6 и введите текст Произведение матриц.
8. В ячейку Е7 введите формулу = МУМНОЖ(А2:С4; Е2:G4). Нажмите клавишу Enter.
9. Формулу в этом случае также вводим как формулу массива. В результате ячейки Е7:G9 будут заполнены элементами единичной матрицы (по главной диагонали будут записаны 1, остальные элементы будут равны 0). Если числа имеют много десятичных знаков, то выделите ячейки Е7:G9 и уменьшите разрядность либо при помощи команды меню Формат/Ячейки/ закладка Число, либо при помощи кнопки Уменьшить разрядность  .
.
ТЕСТОВОЕ ЗАДАНИЕ 1. Решение систем линейных уравнений
Вариант вашего задания задает преподаватель!
Откройте чистый рабочий лист. Переименуйте его в Тест 1. Решите систему линейных уравнений (см. табл. 5) по формулам Крамера.
Формулы Крамера имеют вид:
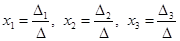 .
.
Здесь D- определитель системы, а D i - вспомогательный определитель, который получается из исходного определителя D путем замены i -го столбца на столбец свободных членов уравнений системы.
Таблица 5
| № | Решить систему | № | Решить систему |
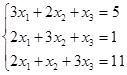
| 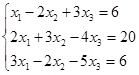
| ||
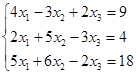
| 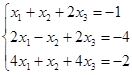
| ||
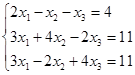
| 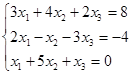
| ||
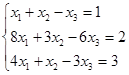
| 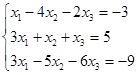
| ||

| 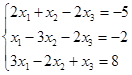
| ||
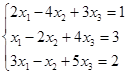
| 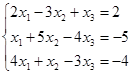
| ||
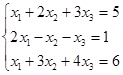
| 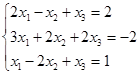
| ||
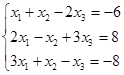
| 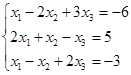
| ||
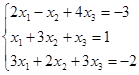
| 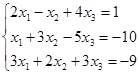
| ||
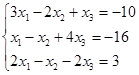
| 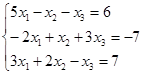
| ||
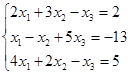
| 
| ||
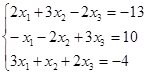
| 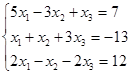
| ||
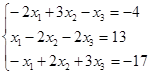
| 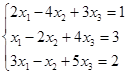
| ||
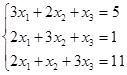
| 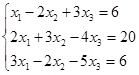
| ||
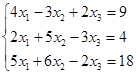
| 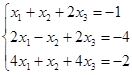
|
ТЕСТОВОЕ ЗАДАНИЕ 2. Решение уравнений, записанных в матричной форме
Вариант вашего задания задает преподаватель!
Откройте чистый рабочий лист. Переименуйте его в Тест 2. Решите матричные уравнения, выбрав свой вариант из таблицы 6.
Примечание. Заданное уравнение нужно свести к одному из двух видов:
1) А Х=В, здесь решение находится по формуле Х=А-1 В
или
2) Х А =В, в этом случае решение находится по формуле Х=В А-1.
Если исходное уравнение имеет вид С Х А =В, то его предварительно приведите к виду: Х А = С-1 В, рассчитайте правую часть системы и затем воспользуйтесь предложенными формулами для нахождения решения системы.
Таблица 6
| № | Уравнение | № | Уравнение |
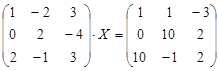
| 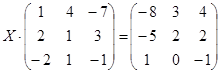
| ||
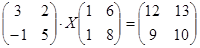
| 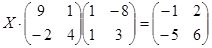
| ||
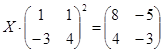
| 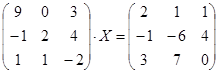
| ||

| 
| ||
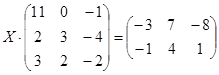
| 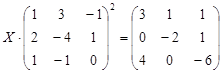
| ||

| 
| ||
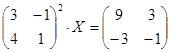
| 
| ||
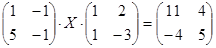
| 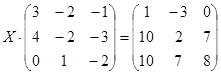
| ||
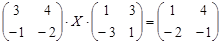
| 
| ||
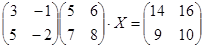
| 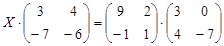
| ||
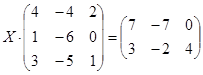
| 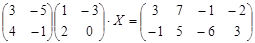
| ||
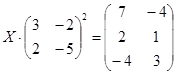
| 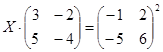
| ||
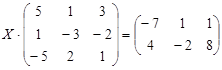
| 
| ||
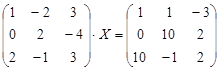
| 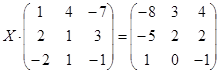
| ||
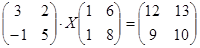
| 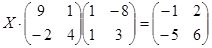
|






