Для нахождения вышеуказанных статистических показателей остановимся на втором примере и рассмотрим его более подробно.
Наиболее часто для нахождения основных статистических показателей применяется способ произведений или уклонений. Применим этот способ к нашему предыдущему примеру:
Классы 5,7 – 6,0 – 6,3 – 6,6 – 6,9 – 7,2 – 7,5 – 7,8 n
Частоты (р) 2 5 12 18 14 6 1 57
Уклонения (а) -3 -2 -1 0 1 2 3
р*а -6 -10 -12 14 12 3 ∑ра = 3
р*а2 18 20 12 14 24 9 ∑ра2 = 97
Первоначально необходимо найти среднее значение признака (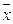
). Эта величина определяется по формуле: 
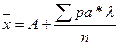, где А – условная средняя вариационного ряда, величина которой приближается к фактической средней. Обычно за условную среднюю (А) принимается середина условного среднего класса, включающего наибольшее количество частот. В нашем примере А будет серединой класса 6,6 – 6,9. от условного среднего класса отмечают в положительную и отрицательную стороны отклонения (а) остальных классов и умножают их на соответствующие частоты. Находим среднюю величину ():
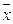Стандартное отклонение (S) является мерой изменчивости признаков. Находится оно по формуле: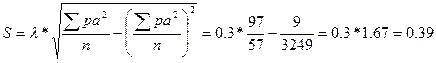 
.
Коэффициент вариации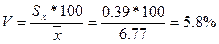 
.
Стандартная ошибка средней 
.
Таким образом, среднее значение искомого признака будет равно: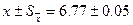 
.
При оценке достоверности различий аналогичных признаков рыб разных популяций, стад и т.п., долгое время пользовались в ихтиологических исследованиях критерием Mdiff > 3 (Правдин, 1966), в последние годы чаще прибегают к нахождению критерия Стьюдента (tst), который можно найти по формул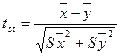е: 
, где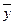 
- среднее значение признака рыб другой популяции и т.д. К примере, по числу жаберных тычинок ленок р. Селенги имеет показатели 
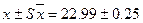(n=36), а в оз. Хубсугул – 23,68 + 0,10 (n = 146). Исходя из этих данных, вычисляем критерий разности Стьюдента по указанному признаку между ними
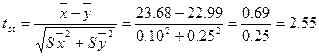
Обычно критерий Стьюдента находится с учетом степеней свободы (f), т.е. сумме значений n обеих выборок за минусом цифра 2. в нашем примере f = 36+146-2=180. По данным приложения 3, критическое значение критерия Стьюдента при первом уровне значимости 5% (вероятностью 95%) и при числе степеней свободы 200 (ближайшее число к 180) составит 1,97, т.е. он меньше фактического значения критерия различия (2,55). В биологических исследованиях различия считаются достоверными, когда фактический критерий различия (t) больше критического при уровне значимости 5% (t05). Если же он равен или меньше критического значения при этом уровне значимости, различия считаются статистически недостоверными. В данном случае различие следует считать достоверным, хотя согласно Mdiff > 3 оно считается нереальным.
Весьма ценно в работах по систематике рыб установление коэффициента СD. Этот коэффициент представляет отношение разности средних к сумме стандартных (среднеквадратичных) отклонений выборок и определяется по формуле: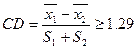 
(Майр, 1971). Коэффициент различия в отличие от критерия Стьюдента оценивает величину различия, а поэтому широко применяется в популяционных исследованиях. Если различия будут более 1,28, то такие различия считаются достоверными, а если не менее 1,5, то такие различия считаются на уровне подвидовых.
В работах по статистике для проверки достоверности исследований рекомендуют вычислять показатель точности опыта (исследования), который выражает величину ошибки средней арифметической в % от самой средней арифметической: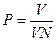 
, где Р – показатель точности опыта, N – объем выборки.
В нашем примере: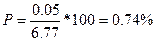 
.
Точность опыта считается удовлетворительной, если Р не превышает 5%. При значении больше 5% рекомендуется увеличить число наблюдений.
