Определение пропускной способности трубопровода

Московский Государственный университет путей сообщения

 

 

Кафедра «Гидравлика и водоснабжение»

 

 

Доцент В.Ф. Бойко.

 

Гидравлический расчет напорных трубопроводов

Методические указания для студентов механических специальностей

 

Москва 2004 г.

Предисловие

Турбулентное движение жидкостей и газов в трубах круглого сечения встречается во многих прикладных задачах (в гидросистемах строительных и дорожных машин, в гидросистемах летательных аппаратов, в водопроводных и вентиляционных трубах, в нефте- и газопроводах, в системах теплофикации и газофикации и т.д.)

Целью данной расчетно-графической работы является более глубокое изучение вопросов турбулентного движения жидкости в трубах на примере гидравлического расчета напорного трубопровода.

Задание содержит несколько связанных между собой задач, составляющих, поверочный гидравлический расчет трубопровода: определение пропускной способности трубопровода, построение пьезометрических линий, определение давления в различных сечениях трубопровода, определение давления насоса, необходимое для увеличения расхода жидкости до заданной величины, определение повышения давления в трубопроводе в случае прикрытия задвижки.

Прежде чем приступить к выполнению расчетно-графической работы необходимо достаточно хорошо изучить соответствующие разделы теоретического курса гидравлики.

Список рекомендуемой литературы приводится в конце данного методического указания.

Расчетно-графическая работа должна быть оформлена в виде расчетно-пояснительной записки (формат А4), сброшюрованной вместе с графическим материалом, выполненном на миллиметровой бумаге карандашом.

Определение пропускной способности трубопровода

В задании требуется определить пропускную способность простого трубопровода (определить какой расход установится в системе) заданных размеров при двух степенях открытия установленной на нем задвижки и при заданном давлении насоса (схема трубопровода дана на бланке задания).

Для решения этого вопроса следует воспользоваться уравнением Д.Бернулли для потока реальной жидкости. Уравнение составляется для двух сечений: за сечение 1 – 1 принимается сечение на выходе из насоса, за сечение 2 – 2 - сечение на выходе из трубопровода (или на поверхности воды в баке, в зависимости от варианта задания). За плоскость сравнения рекомендуется принять горизонтальную плоскость, проходящую через самую нижнюю точку трубопровода (см. схему на бланке задания).

Уравнение запишется в виде:

(1)

Здесь величины - заданы в задании;

γ - удельный вес воды;

g - ускорение свободного падения;

коэффициент Кориолиса, в расчете можно принять =1;

средняя скорость на участке 1;

- сумма гидравлических потерь на участке между сечениями 1 – 1 и 2 – 2.

Запишем уравнение (1) в виде:

В этом уравнении все слагаемые левой части заданы в задании, слагаемые правой части уравнения необходимо определить. Решив уравнение (1) относительно v ₁, в конечном итоге можно определить искомую величину, расход жидкости Q, который установится в системе и который равен

(2)

Здесь s₁ – площадь живого сечения трубопровода на первом участке. С целью определения скорости величина записывается в виде

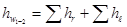(3)

Здесь – сумма потерь напора от местных гидравлических сопротивлений на участке между сечениями 1 – 1 и 2 – 2, – сумма потерь напора по длине на этом же участке.

Величина определяется для каждого местного сопротивления по уравнению

(4)

Здесь ξ – коэффициент местного сопротивления (берется из справочника /1/ в зависимости от вида местного сопротивления);

v – средняя скорость жидкости на участке, где располагается местное сопротивление. Величина для каждого участка трубопровода определяется по уравнению

(5)

Здесь λ – коэффициент гидравлического сопротивления по длине (коэффициент Дарси);

– длина участка трубопровода с соответствующим коэффициентом λ и диаметром d. В задании вся длина трубопровода от сечения 1 – 1 до сечения 2 – 2 состоит из трех участков с длинами _{1, 2}, ₃ c диаметрами соответственно d ₁, d ₂, d ₃ коэффициентами λ ₁, λ ₂, λ ₃ и средними скоростями v ₁, v ₂, v ₃. С учетом изложенного уравнение (3) запишется в виде:

(6)

Здесь – сумма коэффициентов местных сопротивлений соответственно на участках 1, 2, 3.

Подставив выражение для уравнения (6) в уравнение (1), получаем уравнение, в котором шесть неизвестных величин (λ ₁, λ ₂, λ ₃, v ₁, v ₂, v ₃). Нужно выразить v ₂, v ₃ через v ₁ для этого воспользоваться уравнением неразрывности потока , откуда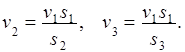

Для определения λ ₁, λ ₂, λ ₃ используется метод приближений. В начале предполагается, что движение воды в трубопроводе относится к четвертой области сопротивления (квадратичной), т.е. поток турбулентный, стенки трубопровода – гидравлически шероховатые. Пользуясь учебной или справочной литературой /1/ принимается для расчета соответствующее уравнение для определения коэффициента гидравлического сопротивления λ Для определения λ в этой области сопротивления рекомендуется воспользоваться уравнением А.Д. Альтшуля

(7)

Здесь k _эк - абсолютная величина так называемой эквивалентной равномерно-зернистой шероховатости. Под эквивалентной шероховатостью понимают равномерно-зернистую шероховатость с такой высотой зерен неровностей (k _эк= k), при которой в области квадратичного сопротивления(где λ _кв зависит только от шероховатости и не зависит от R _е) значение λ _кв одинаково с его значением при естественной шероховатости.

Осредненные численные значения k _эк для труб из различных материалов приведены в табл.1.

Таблица 1

Вид трубы	Состояние трубы	k эк, мм
Стальная сварная	Новая	0,05
Стальная	Старая заржавленная	1,00
Чугунная	Новая	0,30
Чугунная	Бывшая в употреблении	1,00
Бесшовная стальная	Новая	0,03
Бесшовная стальная	Бывшая в употреблении	0,20

 

Коэффициенты ξ для конкретных местных сопротивлений для турбулентного режима движения в области квадратичного сопротивления принимаются из справочного пособия /1/.

С учетом всего изложенного необходимо решить уравнение (1) относительно v ₁. Затем определяются величины Q, v ₂, v ₃. Далее необходимо выполнить проверку правильности предположения о наличии четвертой области сопротивления на всех трех участках трубопровода. Для этого необходимо вычислить для каждого из участков числа Рейнольдса по уравнению

(8)

и сравнить полученные значения 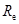с граничным числом Рейнольдса, вычисленному по уравнению

(9)

для каждого из участков трубопровода.

Если полученные значения чисел Рейнольдса 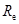больше значений 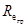,это говорит о правильности предположения о наличии четвертой области сопротивления, расход жидкости определен верно, на этом выполнение п. 1.1 задания завершается.

Для участков трубопровода, для которых не подтвердилось предположение о наличии четвертой области сопротивления, т.е., величину коэффициента гидравлического сопротивления λ следует рассчитать по любому известному уравнению для третьей области сопротивления (по уравнению для переходной области сопротивления).

Для определения λ _пер в этой области можно воспользоваться формулой А.Д. Альтшуля.

(10)

здесь - число Рейнольдса, вычисленное по скорости, полученной по первому приближению для четвертой области сопротивления на соответствующем участке трубопровода. Чтобы избежать арифметических ошибок полезно сравнить коэффициенты гидравлического сопротивления λ _кв для соответствующих участков, вычисленные для четвертой области сопротивления с коэффициентами λ _пер, вычисленными для третьей области сопротивления, и убедиться, что λ _пер > λ _кв.

С полученный значениями λ _пер повторить расчет Q, v ₁, v ₂,. v ₃ и на этом расчет считается законченным. Третье приближение, если, например, поток на каком-то из участков трубопровода не удовлетворяет условию наличия третьей зоны сопротивления, практически не требуется.

В расчетах величин Q (л/с), v (м/с), H (м) рекомендуется ограничиться двумя знаками после запятой.

Для определения расхода жидкости в трубопроводе Q при частично прикрытой задвижке весь расчет следует повторить с учетом нового значения коэффициента местного сопротивления задвижки .

Закончить первый пункт расчетно-графической работы следует составлением сводной таблицы рассчитанных величин по приведенной ниже форме (табл. 2).

Таблица 2

Величины	Значения величин
	При открытой задвижке	При прикрытой задвижке
Q, м3/с
v 1, м/с
v 2, м/с
v 3, м/с
,м
,м
,м