Дешифратор выполняет обратную функцию шифратору, т.е. преобразует двоичный код в унитарный.
Задача. Синтезировать дешифратор на 2 входа.
1. Составим таблицу истинности:
| X1 | X0 | Y3 | Y2 | Y1 | Y0 |
2. Составим СДНФ:
3. Полученные функции не требуют минимизации.
4. Построим комбинационную схему (рис. 12):
Рис. 12. Комбинационная схема дешифратора.
Минимизация функций алгебры логики (ФАЛ)– это процедура нахождения наиболее простого представления ФАЛ в виде суперпозиции функций, составляющих функционально полную систему, при одновременной оптимизации ее технической реализации по некоторым критериям в условиях ряда ограничений. Критериями оптимизации могут быть объем оборудования (количество вентилей, корпусов), габариты, вес, энергопотребление, стоимость, быстродействие, надежность. В качестве ограничений могут выступать допустимые к использованию системы элементов, число элементов в корпусе, коэффициенты объединения по входу и разветвления по выходу логических элементов, необходимость реализации системы ФАЛ, а также ряд перечисленных выше критериев оптимизации.
Учитывая, что такие интегральные схемы дороги, требуют сложной аппаратно-программной поддержки для их программирования, а очень часто в инженерной практике решаются более простые задачи, рассмотрим вопросы минимизации ФАЛ, остановившись на некоторых, нашедших наибольшее распространение, методах минимизации ФАЛ.
К настоящему времени широкое применение получили:
1. Расчетный метод (метод непосредственных преобразований).
2. Расчетно-табличный метод (метод Квайна - МакКласки).
3. Метод Петрика (развитие метода Квайна - МакКласки).
4. Табличный метод (карты Карно).
5. Метод гиперкубов.
6. Метод факторизации.
7. Метод функциональной декомпозиции и др.
В контрольной работе предлагается метод изучить Квайна - МакКласки.
Примеры задач и образцы их решения.
Задача 1.3.1. По заданной карте Карно составить таблицу истинности булевой функции F(A,B,C,D).
Карта Карно:
| CD AB | ||||
Решение.
По известной карте Карно легко составить таблицу истинности булевой функции F:
| A | B | C | D | F(A,B,C,D) |
Серым фоном выделены строки с набором значений, на которых булева функция F равна 1.
Задача 1.3.2. Построить СДНФ по таблице истинности из задачи 1.3.1.
Решение.
Составляем СДНФ, для этого для каждого значения функции равного 1 выписываем элементарную конъюнкцию (конъюнкцию всех переменных), устанавливая отрицание над той переменной, значение которой в соответствующей строке равно 0:
| A | B | C | D | F(A,B,C,D) | M |
M1= 
| |||||
M2= 
| |||||
M3= 
| |||||
M4= 
| |||||
M5=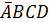 
| |||||
M6= 
| |||||
M7= 
| |||||
M8= 
| |||||
M9= 
| |||||
M10= 
| |||||
Далее записываем дизъюнкцию элементарных конъюнкций, получая СДНФ:
F(A,B,C,D)= M1 
M2 M3 M4 M5 M6 M7 M8 
M9 M10=
= 
Задача 1.3.3. Минимизировать булеву функцию из задачи 1.3.1 методом Квайна - МакКласки.
Решение.
Минимизация булевой функции методом Квайна - МакКласки предполагает на первом этапе выполнение склейки по формуле:
1. Для выделения всех возможных склеек воспользуемся картой Карно. На карте выделим все области, включающие 2, 4, 8 единиц, расположенных рядом. Помните, что карта Карно для 4-х переменных имеет форму тора и все ячейки у нее являются соседними. Обозначим все области 
(рис. 13).
Рис. 13. Выделение склеек.
2. Выделяем ядро. Перечислим области, содержащие 1, которые покрываются лишь один раз, в нашем примере это K1, K2, K3 и K6 (рис. 14).
Рис. 14. Выделение ядра.
3. Перечислим тупиковые ДНФ. В общем случае для этого потребуется использовать функцию Патрика. В нашем примере остались 2 области, не попавшие в ядро, функция Патрика будет записана ровно для одной единицы и будет иметь вид
F= К4 
К5 = 
4. Сформируем кратчайшие ДНФ:
(
–Ядро)
5. Выбираем среди кратчайших ДНФ, содержащие наименьшее число литералов, при равном количестве выбираем любую ДНФ.
Минимальная ДНФ (МДНФ):
F= 
= 
Задача 1.3.4. Изобразить комбинационную схему для полученной в задаче 1.3.3 минимальной ДНФ.
Решение.
Составляем комбинационную схему (рис. 15).
Рис. 15. Комбинационная схема минимальной ДНФ из задачи 1.3.3.
Индивидуальные варианты задач по Теме 1.3 "Минимизация булевых функций".
Задача 1.3.1. По заданной карте Карно составить таблицу истинности булевой функции.
| Вариант 1 | Вариант 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 3 | Вариант 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 5 | Вариант 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 7 | Вариант 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 9 | Вариант 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 11 | Вариант 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 13 | Вариант 14 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 15 | Вариант 16 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 17 | Вариант 18 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 19 | Вариант 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Задача 1.3.2. Построить СДНФ по таблице истинности из задачи 1.3.1.
Задача 1.3.3. Минимизировать булеву функцию из задачи 1.3.1 методом Квайна - МакКласки.
Задача 1.3.4. Изобразите комбинационную схему для полученной в задаче 1.3.3 минимальной ДНФ.
КОНТРОЛЬНАЯ РАБОТА №2 (2 СЕМЕСТР)
