Тема 1.1. Системы счисления (базовая часть).
Цели и задачи.
Изучить правила взаимного перевода чисел между 10-й, 2-й, 8-й и 16-й системами счисления, научиться выполнять действия над числами в различных системах счисления, ознакомиться с форматами представления чисел в памяти ЭВМ.
Справочный материал.
Система счисления (далее - СС) – способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.
Классификация СС по способу изображения чисел:
- позиционные – значение каждой цифры зависит от ее положения в числе
Пример. Арабская десятичная система (123; 321,23).
- непозиционные – цифра не меняет своего значения при изменении её положения в числе
Пример. Римская СС, в которой для каждого числа используется специфическое сочетание символов (IV, VII, IX, XII).
Основание СС - количество цифр p, используемых для изображения числа в позиционной системе.
Пример.
Десятичная СС – основание р =10 (цифры 0 1 2 3 4 5 6 7 8 9).
Двоичная СС – р =2 (цифры 0 1).
Восьмеричная СС – р =8 (цифры 0 1 2 3 4 5 6 7).
Шестнадцатеричная СС – р =16 (цифры и буквы для двузначных чисел - 0 1 2 3 4 5 6 7 8 9 A(10) B(11) C(12) D(13) E(14) F(15)).
Значения цифр числа лежат в пределах от 0 до р -1. Запись любого числа R в СС с основанием р будет представлять собой полином вида
.
Нижний индекс определяет местоположение цифры в числе:
- положительный индекс - у целой части числа (m -разрядов),
- отрицательный индекс - у дробной части числа (s -разрядов).
Очевидно, что аi принимает значение от 0 до р -1.
Число R представляется в виде R =am-1 am-2 …, a-1 a0… a-s
Пример. Для p =10 в виде суммы запишем число 125 = 1*10 (3-1)+2*10(3-2)+5*10(3-3).
Максимальное целое число, которое может быть представлено в m разрядах:
.
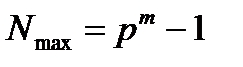Пример. Для р =10 и m =2 максимальное целое число Nmax =102-1=99.
Минимальное значимое (не равное 0) число в s разрядах:
.
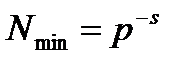Пример. Для р =10 и s =2 минимально значимое число Nmin =10-2=0, 01.
Правила перевода чисел между СС.
Чтобы перевести целое число из одной СС с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы счисления до тех пор, пока не получится частное меньше основания d2. Последнее частное – старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры - это остатки от деления, записываемые в последовательности, обратной их получению.
Примечание: При выполнении переводов чисел из одной СС в другую все необходимые арифметические действия выполняются в той СС, в которой записано переводимое число.
Примеры задач и образцы их решения.
Задача 1.1.1. Переведите 622,325 из 10-й системы счисления в 2-ю, 8-ю и 16-ю системы счисления (с точностью до третьего знака после запятой).
Решение.
Метод перевода чисел из 10-й системы счисления в заданную систему счисления с основанием p различается для целой и дробной части числа.
Целую часть переводят, используя последовательное деление на основание p до получения остатков от деления и частного, меньших, чем p. Результат записывается в виде числа из полученных остатков от деления в обратном порядке.
Дробная часть числа в 10-й системе счисления переводится путем ее умножения на основание p системы счисления до тех пор, пока дробная часть полученных произведений не станет равной нулю, либо до указанного количества знаков после запятой. Результат записывается в виде числа из целых частей полученных произведений в прямом порядке.
Данные методы для перевода числа 622,325 в заданные системы счисления представлены на рис. 1 и 2.
| _622 2 622 _311 2 0 310 _155 2 1 154 _77 2 1 76 _38 2 1 38 _19 2 0 1 8 _9 2 1 8 _4 2 1 4 _2 2 0 2 1 62210=10011011102 | |
| _622 8 616 _77 8 6 72 _9 8 5 8 1 62210=11568 | _622 16 608 _38 16 14 32 2 E 62210=26Е16 |
Рис. 1. Перевод числа 622 из 10-й в 2-ю, 8-ю и 16-ю системы счисления.
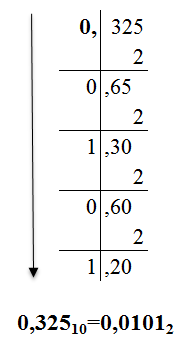
Рис. 2. Перевод числа 0,325 из 10-й в 2-ю системы счисления (с точностью до третьего знака после запятой).
Аналогичным образом (см. рис.2) осуществляется перевод дробной части из 10-й в 8-ю и 16-ю системы счисления. В результате получаем, что
0,32510=0,2468=0,53316.
Соединим целую и дробную части переведенного числа Полный перевод числа 622,325 из 10-й системы счисления в 2-ю, 8-ю и 16-ю системы счисления
Ответ: 622,32510=1001101110,01012=1156,2468=26Е,53316.
Задача 1.1.2. Переведите число 1300А,1В из 16-й системы счисления в 8-ю.
Решение.
Поскольку основания 16-й и 8-й систем счисления являются степенями двойки (16=24, 8=23), то для перевода числа из 16-й в 8-ю используют 2-ю систему счисления. Сначала 16-е число переводят в 2-ю систему счисления, а затем 2-е число переводят в 8-ю систему счисления.
Рассмотрим порядок перевода 16-го числа 1300А,1В в 8-ю систему счисления.
| 1 3 0 0 А, 1 В16 | 1. Запишем число в 16-й системе счисления |
| 0001 0011 0000 0000 1010, 0001 10112 | 2. Каждую цифру 16-го числа переводим в 2-ю систему счисления (см. таблицу 1 Приложения Б) |
| 10011000000001010,000110112 | 3. Запишем число в 2-й системе счисления |
| 010 011 000 000 001 010, 000 110 1102 | 4. Разбиваем 2-е число на триады (группы из трех цифр) от запятой влево и вправо, при нехватке цифр в триаде добавляем 0 |
| 2 3 0 0 1 2, 0 5 58 | 5. Каждую триаду переводим в 8-ю систему счисления (см. таблицу 1 Приложения Б) |
| 230012,0558 | 6. Запишем число в 8-й системе счисления |
Ответ: 1300А,1В16 = 230012,0558.
Задача 1.1.3. Переведите в 10-ю систему счисления числа: 1110100,112; 162,078; АВ, 17816.
Решение.
Чтобы перевести число из заданной системы счисления в 10-ю нужно представить число в виде полинома от основания системы счисления и вычислить его значение. Полином - представление числа в виде суммы его цифр, умноженных на соответствующую степень основания системы счисления:
1110100,11 2 = 1 *26+ 1 *25+ 1 *24+ 0 *23+ 1 *22+ 0 *21+ 0 *20+ 1 *2-1+ 1 *2-2 = =64+32+16+0+4+0+0+0,5+0,25=116,7510;
162,07 8 = 1 *82+ 6 *81+ 2 *80+ 0 *8-1+ 7 *8-2 = 64+48+2+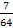 
=114 
;
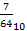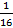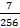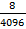АВ, 178 16 = А *161+ В *160+ 1 *16-1+ 7 *16-2+ 8 *16-3 = 10*161+11*160+1*16-1+7*16-2+8*16-3 = =160+11+ 
+ 
+ 
=171 
.
Ответ: 1110100,112 =116,7510; 162,078=114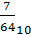 
; АВ, 17816=171 
.
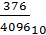Задача 1.1.4. Выполните сложение, вычитание и умножение чисел в указанных системах счисления:
а) 111011012+10010012
б) 1222,078-607,58
в) 1С,516*5,А316
Решение.
Арифметические действия в 2-й, 8-й и 16-й системах счисления выполняются по тем же правилам, что и в 10-й системе счисления. При выполнении этих действий необходимо пользоваться таблицами (см. таблицы 2 и 3 Приложения Б).
Ответ: а) 1001101102; б) 412,378; в)9F,96F16.
Задача 1.1.5. Запишите числа 23 и -125 в двоичном дополнительном коде, интерпретируя их как восьмибитовые целые числа со знаком.
Решение.
Все числа в памяти ЭВМ хранятся в виде двоичных кодов. Диапазон значений зависит от количества k разрядов (знаков, бит), выделяемых для хранения одного числа (обычно оно кратно степени двойки – 4, 8 или 16 бит).
Для целых чисел при записи в память ЭВМ используют дополнительный код. У положительного целого числа дополнительный код совпадает с его представлением в 2-ой системе счисления, дополненным слева до нужного количества разрядов нулями (прямым кодом). Диапазон положительных чисел, для хранения которых выделено k бит, составляет 0..2 k -1, диапазон отрицательных чисел -2 k -1+1..2 k -1 (один бит требуется для хранения знака). Число 1 в крайнем левом разряде дополнительного кода означает, что закодировано отрицательное число.
Получим дополнительный код числа 2310. Для этого сначала переведем 23 из 10-й системы счисления в 2-ю:
2310=101112.
Так как в задании дополнительный код числа нужно интерпретировать как восьмибитовое целое со знаком (тип данных, содержащий 8 бит), добавим слева недостающие до нужного количества нули. В результате получим:
00010111 – это прямой код числа 23.
23 - число положительное, а дополнительный код положительных чисел равен их прямому коду, т.е. дополнительный код 23 равен 00010111.
Рассмотрим число -125. Это число отрицательное. Для записи дополнительного кода отрицательных чисел существует следующий алгоритм
а) сначала записывают число без знака в 2-й системе и дополняют слева нулями до нужного количества разрядов (т.е. получают прямой код для модуля числа);
б) затем получают его обратный код, то есть инвертируют (заменяют 0 на 1, а 1 на 0);
в) к обратному коду прибавляют 1. Полученное значение является дополнительным кодом числа.
Выполним действия по заданному алгоритму:
а) 12510=01111101- прямой код;
б) 10000010 – обратный код;
в) дополнительный код - 10000011=10000010+1.
