6.1 Метод последовательных приближений (метод Пикара)
Метод последовательных приближений состоит из двух этапов. На первом этапе
задача Коши
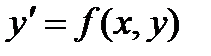 (уравнение), (1)
(уравнение), (1)
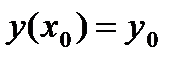 (начальное условие) (2)
(начальное условие) (2)
сводится к эквивалентному интегральному уравнению
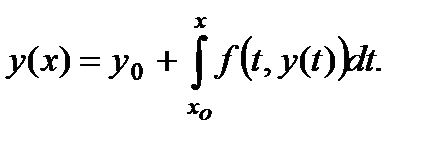 (3)
(3)
Затем решение уравнения (3) ищется с помощью последовательных приближений по формуле
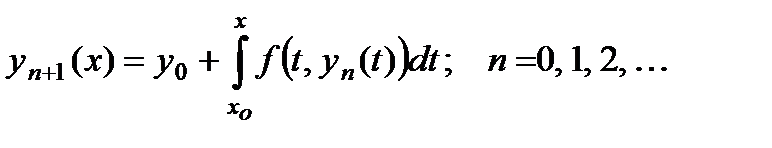
Выбор начального приближения 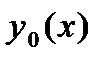 безразличен; проще всего за начальное приближение взять число
безразличен; проще всего за начальное приближение взять число  . Указанный процесс сходится при
. Указанный процесс сходится при 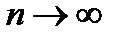 , если выполнены условия теорем из разд. 1.2.
, если выполнены условия теорем из разд. 1.2.
6.2 Метод разложения в ряд Тейлора по независимой переменной
Решение задачи Коши (1) – (2) можно искать в виде ряда Тейлора по степеням
разности (х – х0):
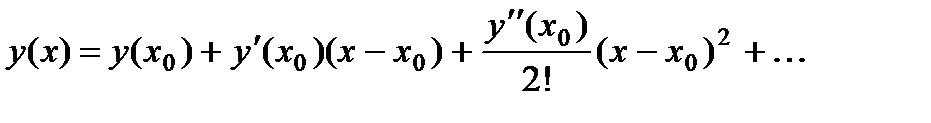 (4)
(4)
Первый коэффициент 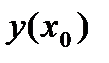 в решении (4) задается начальным условием (2).
в решении (4) задается начальным условием (2).
Последующие значения производных искомой величины в точке х = х0 определяются из уравнения (1) и его следствий (полученных путем последовательного дифференцирования уравнения) с учетом начального условия (2). В частности, полагая в уравнении (1) х = х0 и подставляя значение (2), находим значение первой производной:
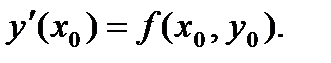 (5)
(5)
Дифференцируя далее уравнение (1), имеем
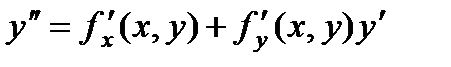 (6)
(6)
Подставив в правую часть этого равенства х = х0, начальное условие (2) и первую производную (5), вычислим значение второй производной:
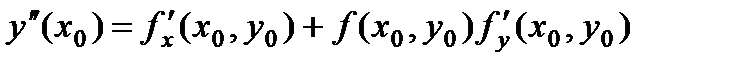 .
.
Подобным образом определяются и последующие производные искомой величины при х = х0.
Полученное данным методом решение (4) обычно можно использовать лишь в
некоторой (достаточно малой) окрестности точки х = х0: 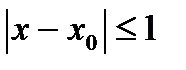 .
.
П р и м е р 11. Найти первые четыре члена разложения решения задачи Коши:
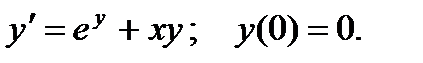
Подставляя в исходное уравнение начальные условия, находим  Дифференцируем исходное уравнение:
Дифференцируем исходное уравнение:
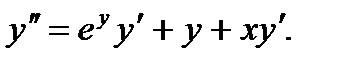
Подставляя сюда начальные условия, находим 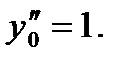 Дифференцируя последнее уравнение и подставляя в полученное выражение для
Дифференцируя последнее уравнение и подставляя в полученное выражение для 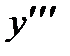 начальные условия, находим
начальные условия, находим  Аналогичным образом
Аналогичным образом 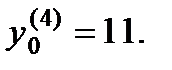 Окончательно
Окончательно
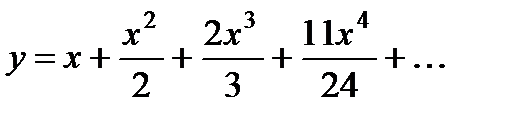 .
.
6.3 Метод регулярного разложения по малому параметру
Рассмотрим уравнение общего вида с параметром 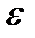 :
:
 (7)
(7)
Пусть функция f может быть представлена в виде степенного ряда по параметру  :
:

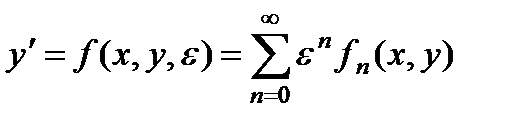 . (8)
. (8)
Решение задачи Коши для уравнения (7) с начальным условием (2) при  ищут
ищут
в виде регулярного разложения по степеням малого параметра:
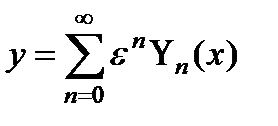 ,
,  . (9)
. (9)
Выражение (9) подставляют в уравнение (7) с учетом представления (8). Затем функции fn разлагают в ряд по малому параметру и собирают члены при одинаковых степенях 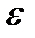 . Приравнивая выражения при одинаковых степенях малого параметра правой и левой частях полученного равенства, приходят к системе уравнений для функций
. Приравнивая выражения при одинаковых степенях малого параметра правой и левой частях полученного равенства, приходят к системе уравнений для функций 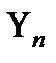 :
:
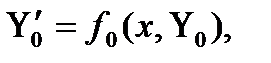 (10)
(10)
 (11)
(11)
Здесь выписаны только первые два уравнения, штрихом обозначены производные по х. Начальные условия для функций 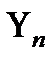 получаются из (2) с учетом разложения (9):
получаются из (2) с учетом разложения (9):
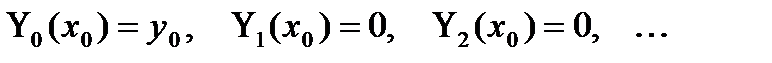
Успех применимости данного метода, в первую очередь, определяется
возможностью построить решение уравнения (10) для главного члена разложения 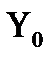 . Важно отметить, что остальные члены разложения
. Важно отметить, что остальные члены разложения 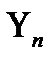 при
при 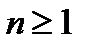 описываются линейными уравнениями с однородными начальными условиями.
описываются линейными уравнениями с однородными начальными условиями.

ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Индивидуальное задание содержит 10 примеров на интегрирование дифференци-
альных уравнений различных типов, рассмотренных в методических указаниях.
Прежде чем приступить к выполнению задания, необходимо приобрести навыки
свободного владения всеми методами решений, приведенными в методических указаниях.
Рекомендуется следующий порядок решения дифференциальных уравнений:
1. Определить тип уравнения и привести его к стандартному виду.
2. Выполнить необходимые при интегрировании данного уравнения квадратуры.
3. Записать ответ в виде общего решения или общего интеграла.
4. Записать дополнительные частные и особые решения.
5. Если решается задача Коши, то по начальным данным следует определить значения постоянной, входящей в состав общего решения.
6. Желательно сделать проверку полученного решения.
Образцы решения всех типовых задач имеются в тексте методических указаний.
В а р и а н т 1
1. 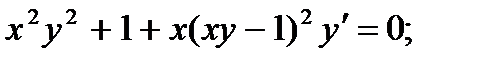 6.
6. 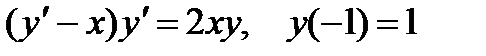 ;
;
2. 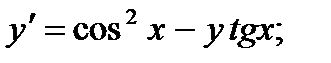 7.
7. 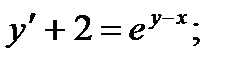
3.  8.
8. 
4.  9.
9. 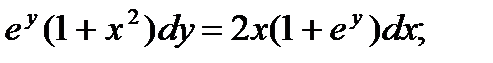
5.  10.
10. 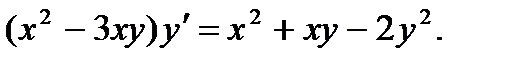
В а р и а н т 2
1.  6.
6. 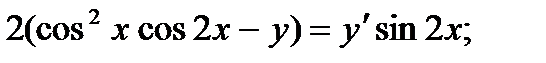
2.  7.
7. 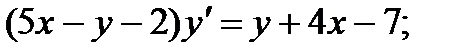



3. 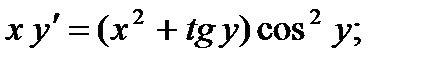 8.
8. 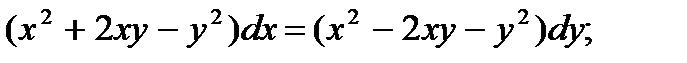
4. 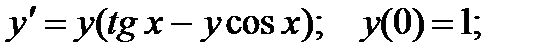 9.
9. 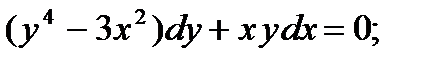
5. 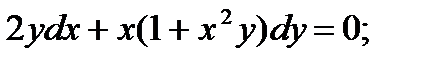 10.
10. 
В а р и а н т 3
1. 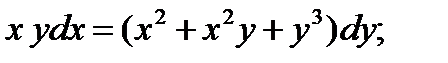 6.
6. 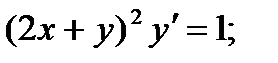
2.  7.
7. 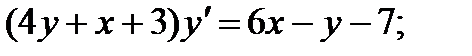
3. 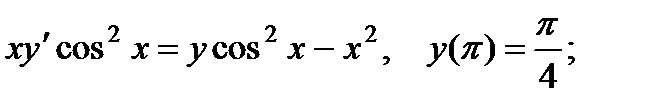 8.
8. 
4.  9.
9. 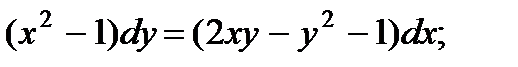
5. 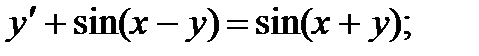 10.
10. 
В а р и а н т 4
1. 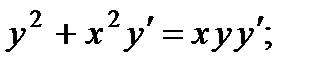 6.
6. 
2. 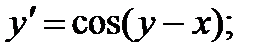 7.
7. 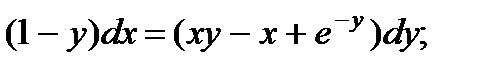
3. 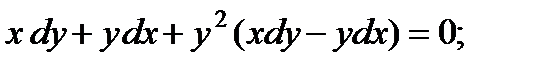 8.
8. 
4.  9.
9. 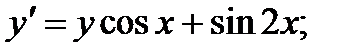
5.  10.
10. 
В а р и а н т 5
1. 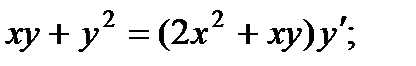 6.
6. 
2. 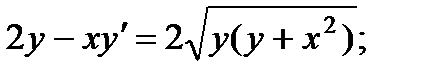 7.
7. 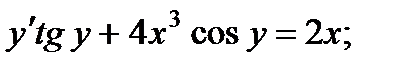
3. 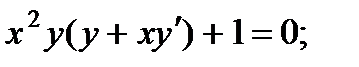 8.
8. 
4. 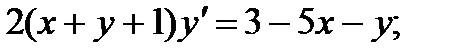 9.
9. 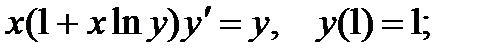
5.  10.
10. 
В а р и а н т 6
1. 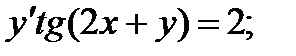 6.
6. 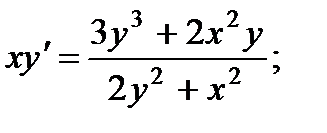
2.  7.
7. 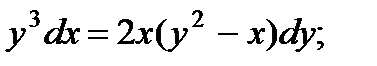
3. 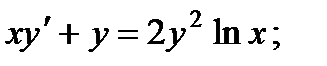 8.
8. 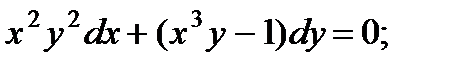
4. 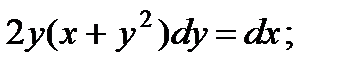 9.
9. 
5. 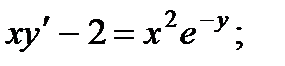 10.
10. 
В а р и а н т 7
1.  6.
6. 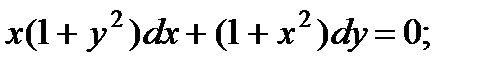
2. 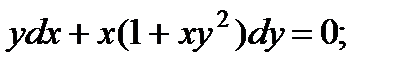 7.
7. 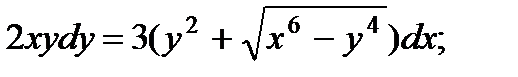
3. 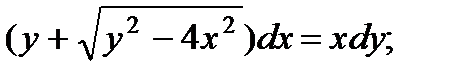 8.
8. 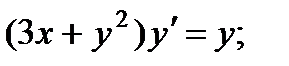
4. 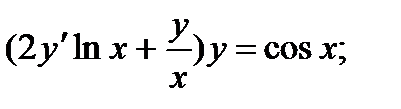 9.
9. 
5.  10.
10. 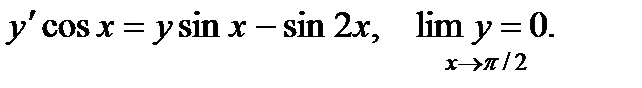
В а р и а н т 8
1. 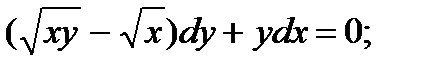 6.
6. 
2.  7.
7. 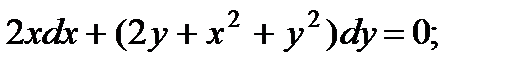
3. 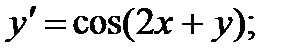 8.
8. 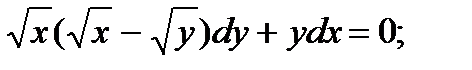
4.  9.
9. 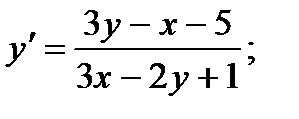
5.  10.
10. 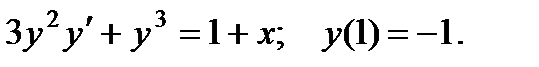
В а р и а н т 9
1. 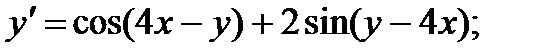 6.
6. 
2.  7.
7. 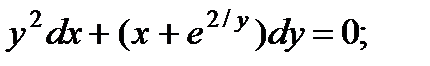
3. 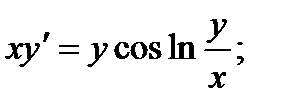 8.
8. 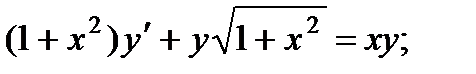
4. 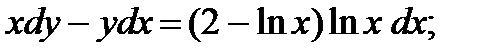 9.
9. 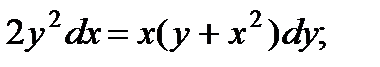
5. 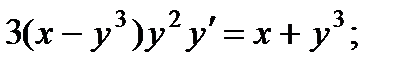 10.
10. 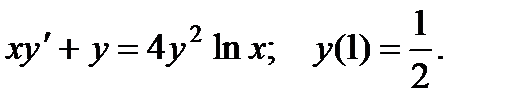
В а р и а н т 10
1. 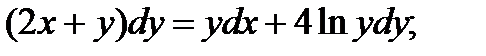 6.
6. 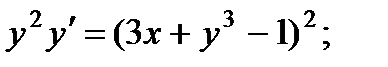
2. 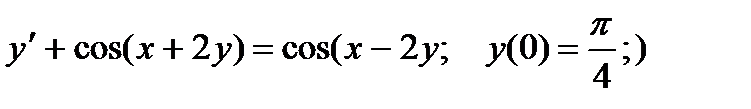 7.
7. 
3. 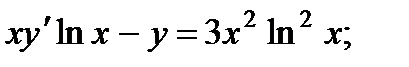 8.
8. 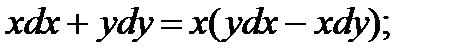
4. 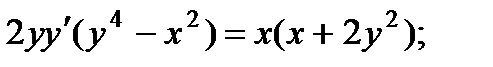 9.
9. 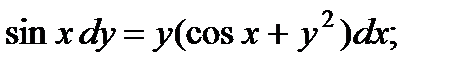
5.  10.
10. 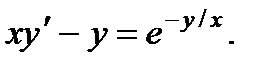
В а р и а н т 11
1. 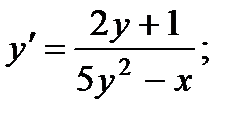 6.
6. 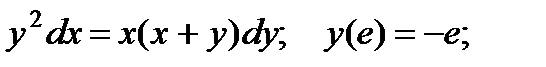
2.  7.
7. 
3. 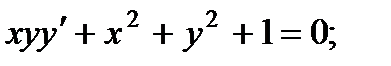 8.
8. 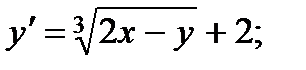
4. 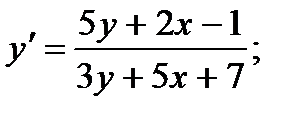 9.
9. 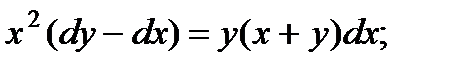
5. 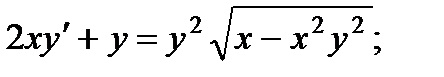 10.
10. 
В а р и а н т 12
1. 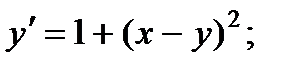 6.
6. 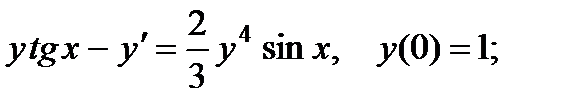
2. 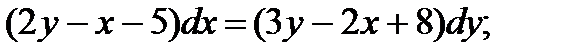 7.
7. 
3.  8.
8. 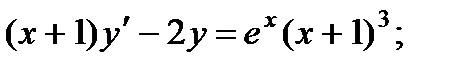
4.  9.
9. 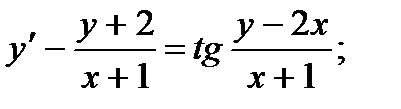
5. 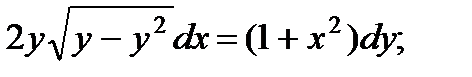 10.
10. 
В а р и а н т 13
1. 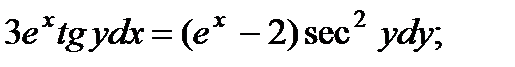 6.
6. 
2.  7.
7. 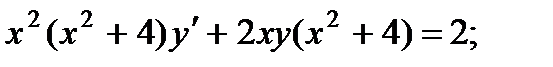
3. 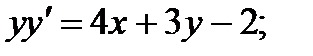 8.
8. 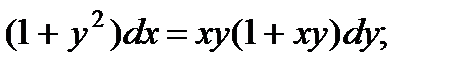
4.  9.
9. 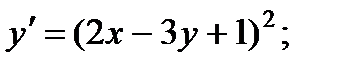
5. 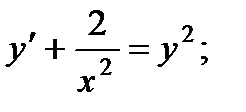 10.
10. 
В а р и а н т 14
1. 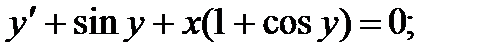 6.
6. 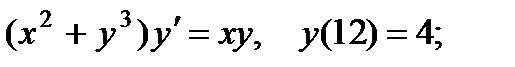
2. 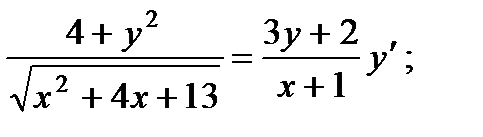 7.
7. 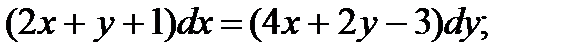
3. 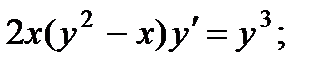 8.
8. 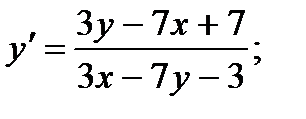
4. 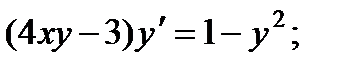 9.
9. 
5. 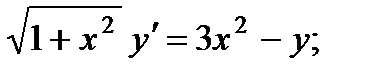 10.
10. 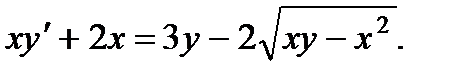
В а р и а н т 15
1. 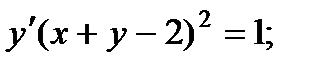 6.
6. 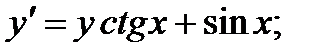
2. 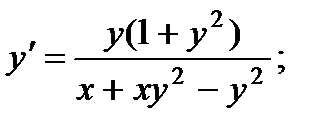 7.
7. 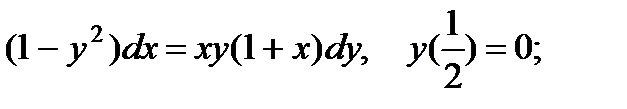
3. 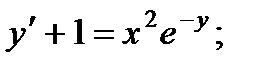 8.
8. 
4.  9.
9. 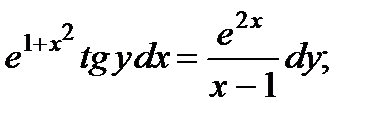
5. 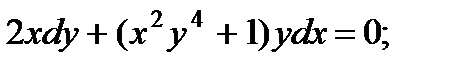 10.
10. 
В а р и а н т 16
1. 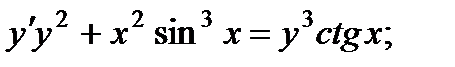
2. 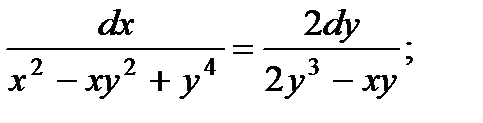
3. 
4. 
5. 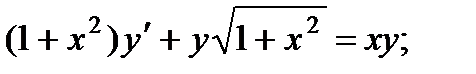
6. 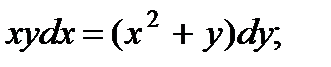
7. 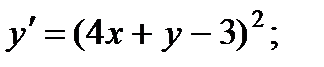
8. 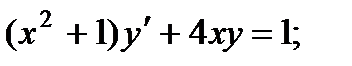
9. 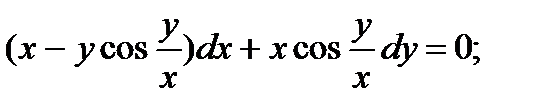
10. 
В а р и а н т 17
1. 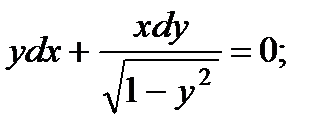 6.
6. 
2.  7.
7. 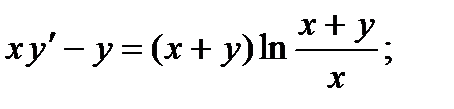
3. 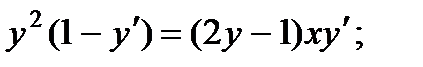 8.
8. 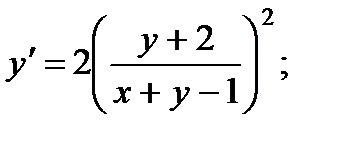
4. 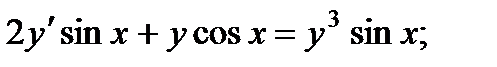 9.
9. 
5.  10.
10. 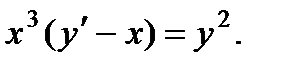
В а р и а н т 18
1. 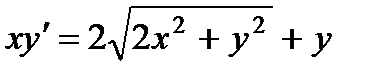 ; 6.
; 6.  ;
;
2. 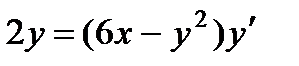 ; 7.
; 7. 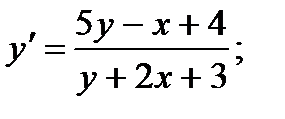
3. 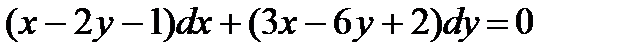 ; 8.
; 8. 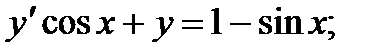
4. 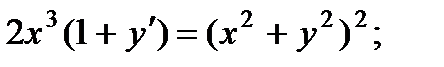 9.
9. 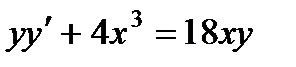 ;
;
5.  10.
10. 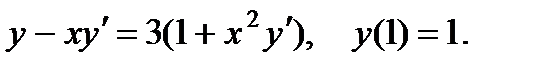
В а р и а н т 19
1.  ; 6.
; 6.  ;
;
2.  ; 7.
; 7. 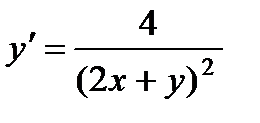 ;
;
3. 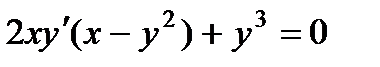 ; 8.
; 8. 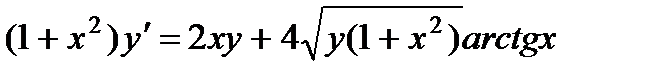 ;
;
4. 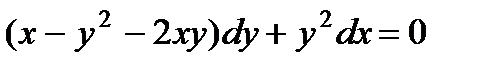 ; 9.
; 9. 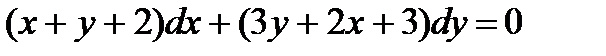 ;
;
5. 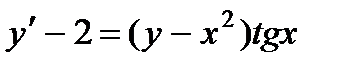 ; 10.
; 10.  .
.
В а р и а н т 20
1. 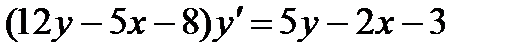 ; 6.
; 6.  ;
;
2. 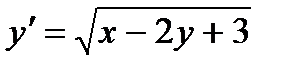 ; 7.
; 7. 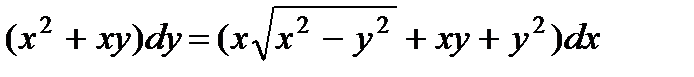 ;
;
3. 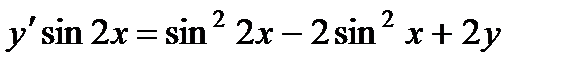 ; 8.
; 8. 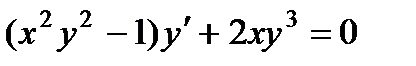 ;
;
4. 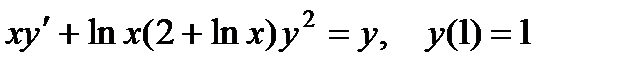 ; 9.
; 9. 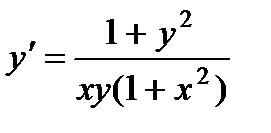 ;
;
5.  ; 10.
; 10. 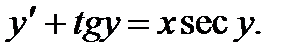
В а р и а н т 21
1. 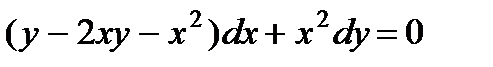 ; 6.
; 6. 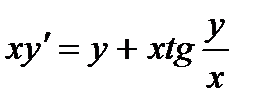 ;
;
2.  ; 7.
; 7. 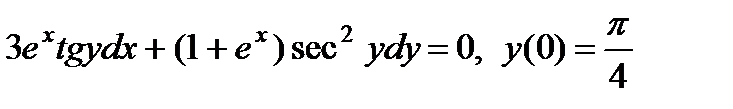 ;
;
3. 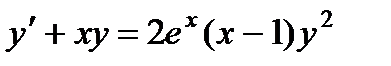 ; 8.
; 8.  ;
;
4.  ; 9.
; 9. 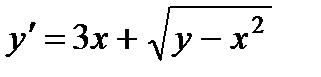 ;
;
5. 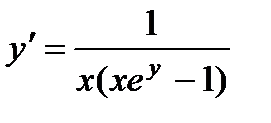 ; 10.
; 10. 
В а р и а н т 22
1. 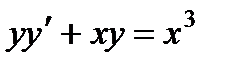 ; 6.
; 6.  ;
;
2. 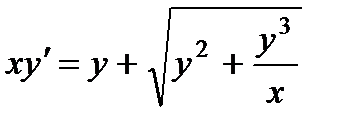 ; 7.
; 7.  ;
;
3. 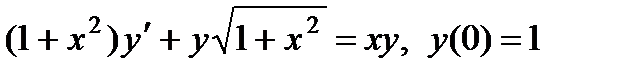 ; 8.
; 8. 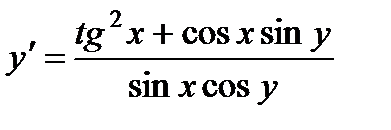 ;
;
4. 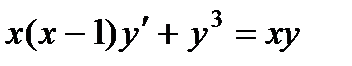 ; 9.
; 9.  ;
;
5. 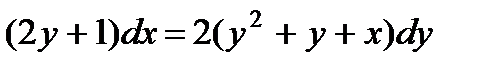 ; 10.
; 10. 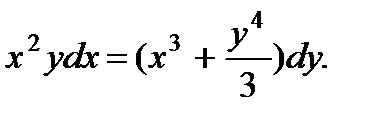
В а р и а н т 23
1. 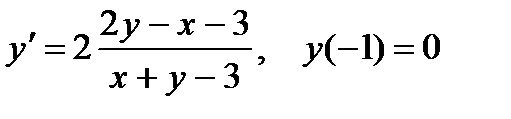 ; 6.
; 6. 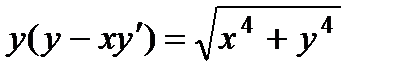 ;
;
2. 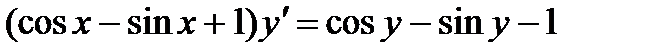 ; 7.
; 7.  ;
;
3.  ; 8.
; 8. 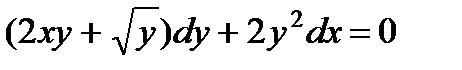 ;
;
4.  ; 9.
; 9. 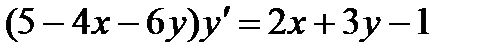 ;
;
5. 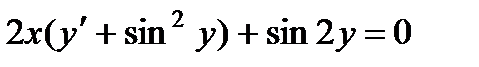 ; 10.
; 10. 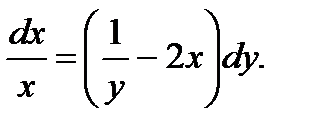
В а р и а н т 24
1. 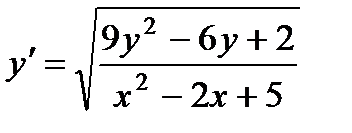 ; 6.
; 6.  ;
;
2. 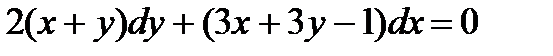 ; 7.
; 7. 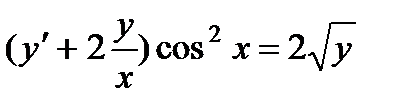 ;
;
3. 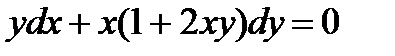 ; 8.
; 8.  ;
;
4. 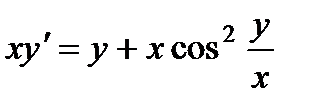 ; 9.
; 9.  ;
;
5.  ; 10.
; 10.  .
.
В а р и а н т 25
1.  ; 6.
; 6. 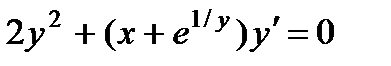 ;
;
2. 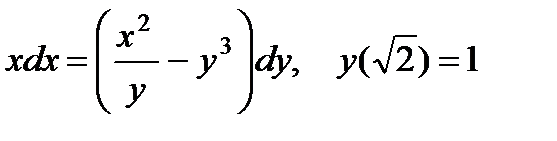 ; 7.
; 7. 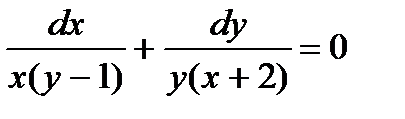 ;
;
3. 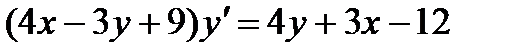 ; 8.
; 8. 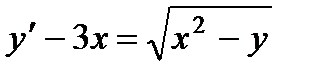 ;
;
4. 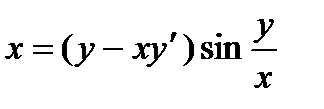 ; 9.
; 9.  ;
;
5. 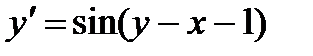 ; 10.
; 10. 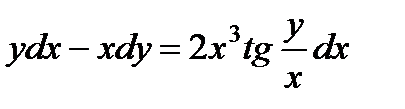 .
.

В а р и а н т 26
1. 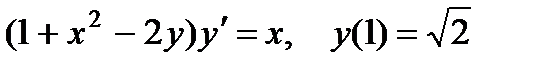 ; 6.
; 6. 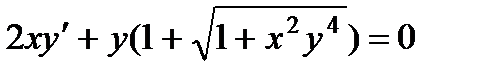 ;
;
2.  ; 7.
; 7. 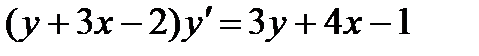 ;
;
3. 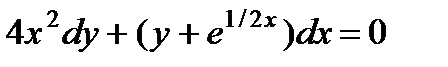 ; 8.
; 8.  ;
;
4. 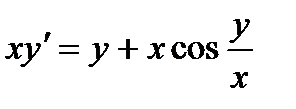 ; 9.
; 9. 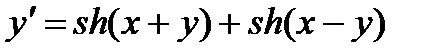 ;
;
5.  ; 10.
; 10. 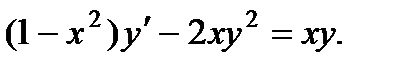
В а р и а н т 27
1. 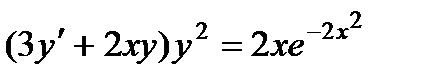 ; 6.
; 6. 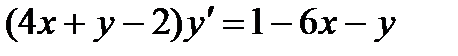 ;
;
2. 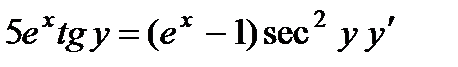 ; 7.
; 7. 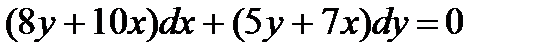 ;
;
3.  ; 8.
; 8.  ;
;
4. 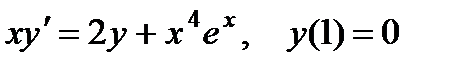 ; 9.
; 9. 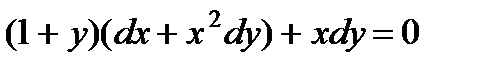 ;
;
5. 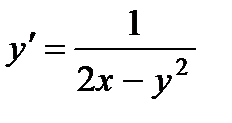 ; 10.
; 10. 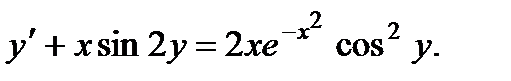
В а р и а н т 28
1. 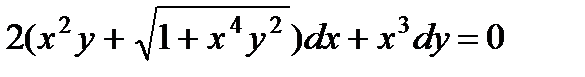 ; 6.
; 6.  ;
;
2.  ; 7.
; 7. 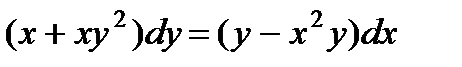 ;
;
3. 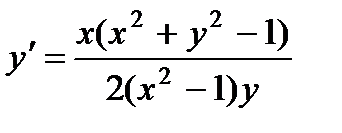 ; 8.
; 8. 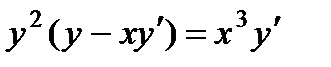 ;
;
4.  ; 9.
; 9.  ;
;
5. 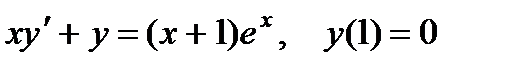 ; 10.
; 10. 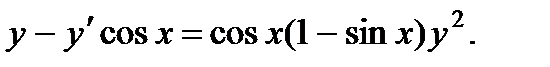
В а р и а н т 29
1.  ; 6.
; 6. 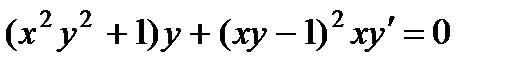 ;
;
2. 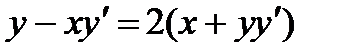 ; 7.
; 7.  ;
;
3. 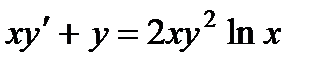 ; 8.
; 8.  ;
;
4. 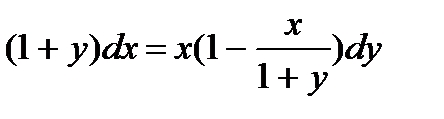 ; 9.
; 9. 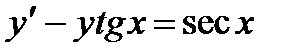 ;
;
5. 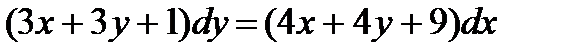 ; 10.
; 10. 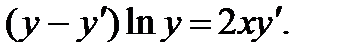
В а р и а н т 30
1. 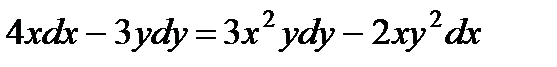 ; 6.
; 6. 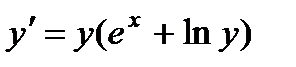 ;
;
2. 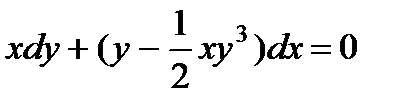 ; 7.
; 7.  ;
;
3. 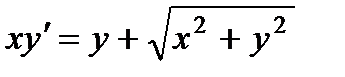 ; 8.
; 8.  ;
;
4. 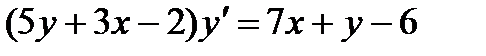 ; 9.
; 9.  ;
;
5. 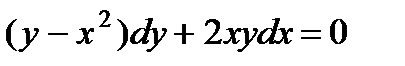 ; 10.
; 10. 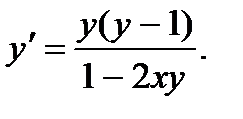
Список литературы
1. Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. – Физматлит, 2005.
2. Федорюк М.В. Обыкновенные дифференциальные уравнения. Издание 3 – URSS: 2009.
3. Задачи и упражнения по математическому анализу для ВТУЗов под редакцией Б.П. Демидовича. – М: “Интеграл – пресс”, 1997.
4. Бабиков Ю.Н. Курс обыкновенных дифференциальных уравнений. – М.: “Высшая
школа”, 1991.
5. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: «РХД», 2000.
6. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. – М:Наука, 1980.
7. Арнольд В.И. Обыкновенные дифференциальные уравнения. – «Регулярная и хаотическая динамика», 2000.

Учебное издание






