При наличии большого числа наблюдений регрессионный анализ начинается с построения эмпирических рядов регрессии. Эмпирический ряд регрессии образуется путем вычисления по значениям одного варьирующего признака X средних значений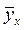 
другого, связанного корреляционно с X признака Y. Иными словами, построение эмпирических рядов регрессии сводится к нахождению групповых средних 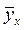и 
из соответствующих значений признаков Y и X.
Эмпирический ряд регрессии – это двойной ряд чисел, которые можно изобразить точками на плоскости, а затем, соединив эти точки отрезками прямой, получить эмпирическую линию регрессии. Эмпирические ряды регрессии, особенно их графики, называемые линиями регрессии, дают наглядное представление о форме и тесноте корреляционной зависимости между варьирующими признаками [5].
Выравнивание эмпирических рядов регрессии. Графики эмпирических рядов регрессии оказываются, как правило, не плавно идущими, а ломаными линиями. Это объясняется тем, что наряду с главными причинами, определяющими общую закономерность в изменчивости коррелируемых признаков, на их величине сказывается влияние многочисленных второстепенных причин, вызывающих случайные колебания узловых точек регрессии. Чтобы выявить основную тенденцию (тренд) сопряженной вариации коррелируемых признаков, нужно заменить ломаные линии на гладкие, плавно идущие линии регрессии. Процесс замены ломаных линий на плавно идущие называют выравниванием эмпирических рядов и линий регрессий.
Графический способ выравнивания. Это наиболее простой способ, не требующий вычислительной работы. Его сущность сводится к следующему. Эмпирический ряд регрессии изображают в виде графика в системе прямоугольных координат. Затем визуально намечаются средние точки регрессии, по которым с помощью линейки или лекала проводят сплошную линию. Недостаток этого способа очевиден: он не исключает влияние индивидуальных свойств исследователя на результаты выравнивания эмпирических линий регрессии. Поэтому в тех случаях, когда необходима более высокая точность при замене ломанных линий регрессии на плавно идущие, используют другие способы выравнивания эмпирических рядов.
Способ скользящей средней. Суть этого способа сводится к последовательному вычислению средних арифметических из двух или трех соседних членов эмпирического ряда. Этот способ особенно удобен в тех случаях, когда эмпирический ряд представлен большим числом членов, так что потеря двух из них – крайних, что неизбежно при этом способе выравнивания, заметно не отразится на его структуре.
Метод наименьших квадратов. Этот способ предложен в начале XIX столетия А.М. Лежандром и независимо от него К. Гауссом. Он позволяет наиболее точно выравнивать эмпирические ряды. Этот метод, как было показано выше, основан на предположении, что сумма квадратов отклонений вариант xi от их средней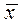 
есть величина минимальная, т.е. 
. Отсюда и название метода, который применяется не только в экологии, но и в технике. Метод наименьших квадратов объективен и универсален, его применяют в самых различных случаях при отыскании эмпирических уравнений рядов регрессии и определении их параметров.
Требование метода наименьших квадратов заключается в том, что теоретические точки линии регрессии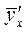 
должны быть получены таким образом, чтобы сумма квадратов отклонений от этих точек для эмпирических наблюдений yi была минимальной, т.е.
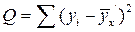(11)
Вычисляя в соответствии с принципами математического анализа минимум этого выражения и определенным образом преобразуя его, можно получить систему так называемых нормальных уравнений, в которых неизвестными величинами оказываются искомые параметры уравнения регрессии, а известные коэффициенты определяются эмпирическими величинами признаков, обычно суммами их значений и их перекрестных произведений.
Множественная линейная регрессия. Зависимость между несколькими переменными величинами принято выражать уравнением множественной регрессии, которая может быть линейной и нелинейной. В простейшем виде множественная регрессия выражается уравнением с двумя независимыми переменными величинами (x, z) 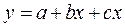(12):
(12)
где a – свободный член уравнения; b и c – параметры уравнения. Для нахождения параметров уравнения (11) (по способу наименьших квадратов) применяют следующую систему нормальных уравнений:
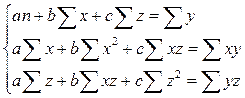
Полигон и гистограмма
Для наглядности строят различные графики статистического распределения.
По данным дискретного вариационного ряда строят полигон частот или относительных частот.
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2),..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки (xi; ni) соединяют отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1; W1), (x2; W2),..., (xk; Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им относительные частоты Wi. Точки (xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni / h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni / h.
Площадь i - го частичного прямоугольника равна hni / h = ni - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).
2 Статистический анализ зависимости
Определение зависимости величины средней заработной платы населения от количества часов работы в неделю. Исходные данные представлены в таблице 1.
Таблица 1.
Исходные данные
| № | средняя з/п | часы/неделя |
Первым шагом при решении данной задачи необходимо ранжировать данные в соответствии с правилами ранжирования. Для начала присвоим ранги отработанным часам в неделю. В данной выборке наименьшему числу часов соответствует 20 часов, присваиваем ранг 1.
В таком же порядке присваиваем следующие ранги по отработанным часам. Следующий значение равно 30 часам, присваиваем ранг 2.
Следующее значение 40 часов, в выборке имеется 4 человека с таким значением. Вычисляем и присваиваем им средний ранг:
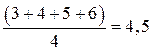
Один человек работает 42 часа в неделю, присваиваем ранг 7. Следующему человеку, который работает 43 часа, присваиваем ранг 8.
По 45 часов в неделю работают 2 человека. Их средний ранг будет равен:
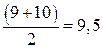
Один человек работает 46 часов в неделю, присваиваем ранг 11.
3 человека работают по 48 часов, вычислим и присвоим им следующий ранг:
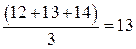
По 49 часов в неделю работают три человека, их средний ранг равен:
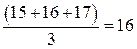
Три человека работают по 50 часов, вычислим и присвоим им следующий ранг:
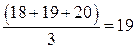
По 55 часов в неделю работают три человека, их средний ранг равен:
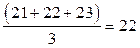
Два человека работает по 58 часов, им присваиваем средний ранг:
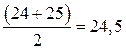
По 60 часов в неделю работают два человека, их средний ранг равен:
64 часа в неделю работает лишь один человек, присваиваем ему ранг 28.
По 65 часов в неделю работают два человека, их средний ранг равен:
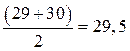
Результаты ранжирования по количеству отработанных часов представлены в таблице 2.
Таблица 2.
Ранжирование отработанных часов
| № | часы/неделя | ранг Х |
| 9,5 | ||
| 4,5 | ||
| 29,5 | ||
| 4,5 | ||
| 26,5 | ||
| 4,5 | ||
| 9,5 | ||
| 24,5 | ||
| 4,5 | ||
Продолжение таблицы 2.
| 26,5 | ||
| 29,5 | ||
Следующим шагом будем по аналогии необходимо ранжировать данные по средней заработной плате. В таблице 3 представлен результат ранжирования.
Таблица 3.
Ранжирование данных
| № | часы/неделя | средняя з/п | ранг Х | ранг Y |
| 9,5 | 8,5 | |||
| 10,5 | ||||
| 6,5 | ||||
| 4,5 | 4,5 | |||
| 8,5 | ||||
| 15,5 | ||||
| 22,5 | ||||
| 29,5 | 28,5 | |||
| 15,5 | ||||
| 4,5 | 6,5 | |||
| 26,5 | ||||
| 4,5 | ||||
| 9,5 | ||||
| 24,5 | ||||
| 4,5 | 4,5 | |||
| 26,5 | ||||
| 10,5 |
Продолжение таблицы 3.
| 29,5 | 28,5 | |||
| 22,5 |
Далее в соответствии по алгоритму, найдем разность рангов и возведем её в квадрат. Результаты данных действий представлены в таблице 4.
Таблица 4.
Разность рангов и возведение её в квадрат
| № | часы/неделя | средняя з/п | ранг Х | ранг Y | X-Y | d^2 |
| 9,5 | 8,5 | |||||
| 10,5 | 2,5 | 6,25 | ||||
| 6,5 | 0,5 | 0,25 | ||||
| 4,5 | 4,5 | |||||
| 8,5 | 7,5 | 56,25 | ||||
| 15,5 | 0,5 | 0,25 | ||||
| -5 | ||||||
| -22 | ||||||
| 22,5 | -0,5 | 0,25 | ||||
| 29,5 | 28,5 | |||||
| 15,5 | -4,5 | 20,25 | ||||
| 4,5 | 6,5 | -2 | ||||
| 26,5 | 1,5 | 2,25 | ||||
| -7 | ||||||
| 4,5 | 2,5 | 6,25 | ||||
| 9,5 | -3,5 | 12,25 | ||||
| 24,5 | -2,5 | 6,25 | ||||
| 4,5 | 4,5 | |||||
| -1 | ||||||
| 26,5 | -3,5 | 12,25 | ||||
| 10,5 | 2,5 | 6,25 | ||||
| -5 | ||||||
| 29,5 | 28,5 | |||||
| 22,5 | -0,5 | 0,25 |
Далее необходимо найти сумму столбца d^2. Данная сумма равна 783,25.
Следующим действием найдем коэффициент ранговой корреляции Спирмена:
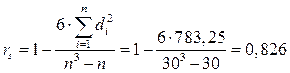
Итак, коэффициент ранговой корреляции Спирмена равен 0,826. Следовательно, зависимость прямая, сильная.
Рассмотрим построение однофакторного уравнения регрессии зависимости средней заработной платы (Y) от количества отработанных часов в неделю (Х)
Сопоставление данных параллельных рядов признаков Х и Y показывает, что с возрастанием признака Х, растет результативный признак Y (средняя заработная плата). Следовательно, между Х и Y существует прямолинейная зависимость.
Для уточнения связи между рассматриваемыми признаками используем графический метод. Построим диаграмму рассеивания.
Рис. 2 – Диаграмма рассеивания
Анализируя линию, можно предположить, что увеличение размера средней заработной платы Y идет равномерно, пропорционально возрастанию количества отработанных часов в неделю Х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (линия на рисунке 2), которая может быть выражена простым линейным уравнением регрессии:
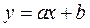(13)
Пользуясь расчетными значениями, исчислим параметры для данного уравнения регрессии по формулам 14 и 15.
(14)
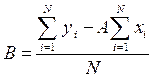
(15)
Подставив исходные данные в формулы, получим коэффициенты для данного уравнения:
А= 487,426;
В= -1568,445.
Следовательно, регрессионная модель может быть записана в виде конкретного простого уравнения регрессии:
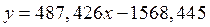
Рассчитаем коэффициент корреляции по следующей формуле (16):
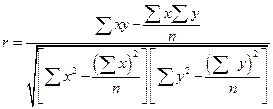
(16)
Подставив исходные данные в формулы, получим коэффициент:
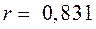
Положительное значение коэффициента корреляции (0,831) свидетельствует об прямой зависимости между количеством отработанных часов в неделю и средней заработной платой. Т.к. r= 0,831, то чем ближе к 1 значение коэффициента корреляции, тем теснее связь. Т.к. коэффициент корреляции свыше |0,7|, значит, связь тесная между изучаемыми признаками: количеством отработанных часов в неделю и средней заработной платы.
Выборочная дисперсия находится по формуле (17):
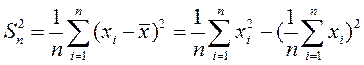
(17)
Подставив в формулу исходные значения, получаем 96,89.
Исправленная дисперсия рассчитывается по формуле (18):
(18)
И она равна 100,236.
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины. Определяется по формуле 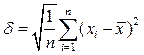(19):
(19)
Предварительно вычислив выборочное среднее и подставив все значения в формулу, вычислим, что среднеквадратичное отклонение равно 9,843.
Для того чтобы найти медиану числового ряда необходимо упорядочить их, как показано в таблице 5. Далее определим число, расположенное посередине числового ряда, если количество чисел четное, возьмем два числа находящихся посередине ряда и найдем их среднее значение, оно и будет являться медианой числового ряда.
Мода – это значение выборки, которое встречается наиболее часто. Мода полезна при анализе нечисловых данных.
- если в выборке нет повторяющихся значений, у нее нет моды;
- если в выборке несколько значений повторяются с одинаковой частотой, у такой выборки несколько мод. Результаты данных действий представлены в таблице 5.
Таблица 5.
Медианы и моды
| № | часы/неделя | средняя з/п | |
Продолжение таблицы 5.
| Медианы = | Медианы = | ||
| Моды = | Моды = | 15000,20000, 22000, 28000 |
Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Поскольку в приводимом примере факторный признак представлен всего пятью вариантами повторяющихся значений, достаточно в первом столбце корреляционной таблицы выписать эти результаты. Для результативного признака необходимо определить величину интервала группировки. Это можно сделать с помощью формулы Стержэсса (20):
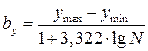. (20)
В нашем случае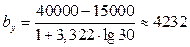 
В строку 2 поместим среднюю заработную плату, при этом удалив повторяющиеся, в столбец В помести количество отработанных часов в неделю, при этом также удалив повторяющиеся. Далее разобьем столбцы с заработной платой на интервалы, прибавляя к начальной сумме 4232. После этого заполним таблицу исходя из входных данных (сколько получает человек в определенном интервале заработной платы и за сколько отработанных часов). Результаты заполнения данной таблицы представлены на рисунке 3.
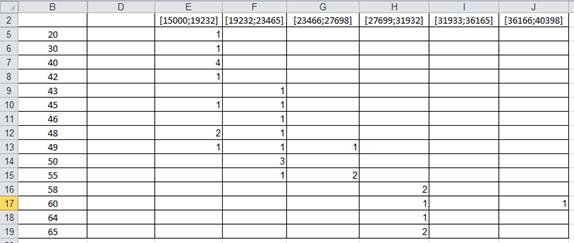
Рис. 3 – Заполненная таблица корреляции
Используя данные корреляционной таблицы, построим гистограммы, полигоны и графики эмпирических функций распределения для X и Y.
Гистограмма для Х представлена на рисунке 4.
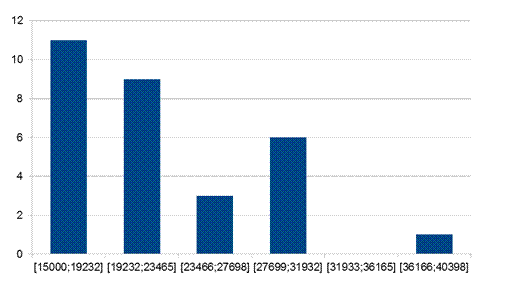
Рис. 4 – Гистограмма по Х
Гистограмма для Y представлена на рисунке 5.
.
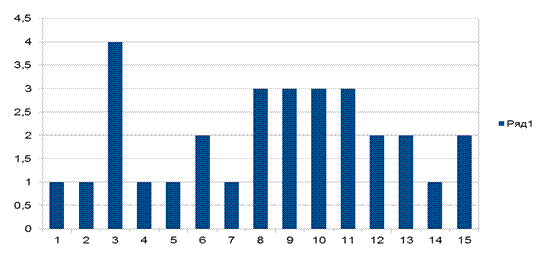Рис. 5 – Гистограмма по Y
Полигоны для X и Y представлены на рисунке 6 и 7.
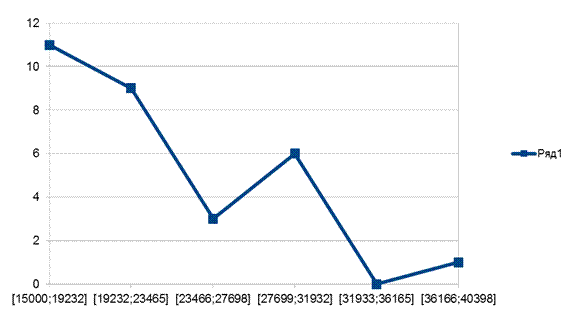
Рис. 6 – Полигон для Х
Рис. 7 – Полигон для Y
3 Решение с помощью MS Excel
На рисунках 8 -15 показано выполнение вышеуказанных действий в MS Excel.
Рис. 8 – Регрессионный метод
Рис. 9 – Таблица корреляции
Заключение
В данной курсовой работе, посвященной регрессионному анализу, было рассказано о вычислении коэффициента ранговой корреляции Спирмена, было раскрыто определение корреляционной связи, рассмотрены этапы корреляционного анализа, рассмотрена парная регрессия, описан метод наименьших квадратов. Также в ходе работы был вычислен коэффициент ранговой корреляции Спирмена на примере распределений работы в неделю и средней заработной платы. В результате проделанной работы мы получили прямую зависимость: чем больше работы работы в неделю, тем больше уровень средней заработной платы. Были построены полигоны и гистограммы. Все цели курсовой работы достигнуты, а задачи выполнены. Обычно оптимизируется одна функция, наиболее важная с точки зрения цели исследования, при ограничениях, налагаемых другими функциями. Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров. Для этого и используется корреляционный анализ.
С использованием результатов корреляционного анализа исследователь может делать определённые выводы о наличии и характере взаимозависимости, что уже само по себе может представлять существенную информацию об исследуемом объекте. Результаты могут подсказать и направление дальнейших исследований, и совокупность требуемых методов, в том числе статистических, необходимых для более полного изучения объекта.
Особенно реальную пользу применение аппарата корреляционного анализа может принести на стадии ранних исследований в областях, где характеры причин определённых явлений ещё недостаточно понятны. Это может касаться изучения очень сложных систем различного характера: как технических, так и социальных.
Необходимо отметить: уравнения регрессии позволяют прогнозировать возможные значения зависимой переменной на основании известных величин аргумента. При этом, однако, не следует экстраполировать регрессию за пределы проведенных опытов, так как она может менять свое направление. Область применения уравнений регрессии лучше ограничить теми данными, на которых получены эмпирические уравнения. Это предостережет исследователя от возможных ошибок.
В данной курсовой работе, автор считает, что хорошо выполнен регрессионный анализ и также проведен анализ ранговой корреляции Спирмена. Сделана диаграмма рассеивания.
Трудности вызвали построение полигон и гистограмм. Но с помощью интернета, просмотрев теорию построения полигон, автор справился с этой задачей, хотя нет уверенности в ее правильности. Были не обозначены оси гистограмм.
Значимость этой проделанной работы в том, что позволило узнать о небольшой части жизни окружающих меня людей, так как пообщавшись с многими людьми, проведен опрос. Проведен анализ что принесло не мало пользы для умственной работы.
Список литературы
1. Глинский В.В., Ионин В.Г. Статистический анализ. Учебное пособие. Издание 2-е, переработанное и дополненое. – М.: Информационно-издательский дом «Филинъ», 2004. — 479 с.
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник/Под ред. И.И. Елисеевой. – 4-е издание, переработанное и дополненное. – Москва: Финансы и Статистика, 2002. – 480 с.
3. Черепанов В.С., Булатова Е.Г. Методы исследований в социальных и гуманитарных науках: Учебное пособие. В 2 ч. Ч. 2. – Ижевск: Изд-во ИжГТУ, 2008. – 172 с.
4. Н.Ш. Кремер, Теория вероятностей и математическая статистика", Глава 12 "Корреляционный анализ".
5. Сидоренко А.В. Математические методы обработки результатов в психологии. СПб.: ООО «Речь», 2006. – 350с.
