Парная и множественная регрессия

Оглавление

c.

1 Регрессионный анализ 4

1.1 Парная и множественная регрессия 5

1.2 Линейная регрессия 6

1.3 Построение эмпирических рядов регрессии 10

1.4 Полигон и гистограмма 13

2 Статистический анализ зависимости 14

3 Решение с помощью MS Excel 27

Заключение 28

Список литературы 29

Введение

Цель данной курсовой работы – провести статистический анализ зависимости величины средней заработной платы населения от количества часов работы в неделю.

Решение данной задачи позволит определить существует ли зависимость между количеством часов работы в неделю и размером средней заработной платы, а рассмотрение статистического анализа позволит осуществлять поиск зависимости переменных друг от друга в различных областях деятельности человека.

В задачах математического программирования нужно определить значение целевой функции. Практически в любой ситуации обнаруживается несколько целей противоречащих друг другу. Поэтому для эффективного решения любой из задач в первую очередь необходимо построить математическую модель, которую затем нужно оптимизировать, предварительно выбрав подходящий для этого метод.

Различных форм и видов корреляционных связей много. Задача сводится к тому, чтобы в каждом конкретном случае выявить форму связи и выразить ее соответствующим корреляционным уравнением, что позволяет предвидеть возможные изменения одного признака Y на основании известных изменений другого X, связанного с первым корреляционно.

В ходе написания курсовой работы будут решены следующие задачи:

- раскрыть понятие регрессионного анализа;

- построить диаграмму рассеивания;

- рассмотреть понятия парной регрессии и корреляции.

Во введении раскрывается актуальность темы курсовой работы, формируются цели и задачи. В теоретической части будут рассмотрены методы и этапы корреляционного анализа. В заключении дается общий вывод по проделанной работе.

1 Регрессионный анализ

Статистика – это наука, которая занимается получением, обработкой, а также анализом данных и публикацией информации, характеризующей количественные закономерности жизни общества в неразрывной связи с их качественным содержанием. В более узком смысле статистика – это совокупность данных о каком-либо процессе или явлении. Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных – результатов наблюдений [1].

Теория вероятностей – раздел математики, в котором по данным вероятностям одних случайных событий находят вероятности других событий, связанных каким-либо образом с первыми. Теория вероятностей изучает также случайные величины и случайные процессы. Одна из основных задач теории вероятностей состоит в выяснении закономерностей, возникающих при взаимодействии случайных факторов.

Зависимость между переменными величинами x и y может быть описана разными способами. В частности, любую форму связи можно выразить уравнением общего вида 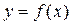, где y рассматривается в качестве зависимой переменной, или функции от другой – независимой переменной величины x, называемой аргументом. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком. Изменение функции в зависимости от изменения одного или нескольких аргументов называется регрессией. Все средства, применяемые для описания корреляционных связей, составляет содержание регрессионногоанализа.

Для выражения регрессии служат корреляционные уравнения, или уравнения регрессии, эмпирические и теоретически вычисленные ряды регрессии, их графики, называемые линиями регрессии, а также коэффициенты линейной и нелинейной регрессии.

Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение усредненных значений 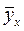признака Y при изменении значений x_i признака X, и, наоборот, показывают изменение средних значений 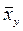признака X по измененным значениям y_i признака Y. Исключение составляют временные ряды, или ряды динамики, показывающие изменение признаков во времени. Регрессия таких рядов является односторонней.

Различных форм и видов корреляционных связей много. Задача сводится к тому, чтобы в каждом конкретном случае выявить форму связи и выразить ее соответствующим корреляционным уравнением, что позволяет предвидеть возможные изменения одного признака Y на основании известных изменений другого X, связанного с первым корреляционно [2].

 

Парная и множественная регрессия

Парная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у, рассматривается как функция одной независимой (объясняющей) переменной х, формула 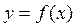(1):

(1)

Основные гипотезы, лежащие в основе классической линейной модели парной регрессии:

1. Спецификация модели

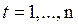
2. детерминированная величина

Вектор 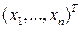не коллинеарен вектору

3. 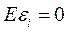, т.е. математическое ожидание ошибок (остатков) равно нулю.

4. неизменность дисперсий ошибок (остатков), дисперсия не зависит от i.

5. 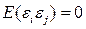при 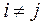некоррелированность ошибок для разных наблюдений

6. Ошибки имеют совместное нормальное распределение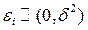

Комментарии к основным гипотезам:

Спецификация модели отражает наше представление о механизме зависимости от и сам выбор объясняющей переменной .

Условие 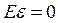означает, что 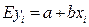, т.е. при фиксированном среднее ожидаемое значение равно a+bx_i.

Условие 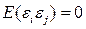при 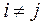указывает на некоррелированность ошибок для разных наблюдений. Это условие часто нарушается в случае, когда наши данные являются временными рядами.

В случае, когда это условие не выполняется, говорят об автокорреляции ошибок.

 

Линейная регрессия

Уравнение регрессии. Результаты наблюдений, проведенных над тем или иным биологическим объектом по корреляционно связанным признакам x и y, можно изобразить точками на плоскости, построив систему прямоугольных координат. В результате получается некая диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующими признаками. Довольно часто эта связь выглядит в виде прямой или может быть аппроксимирована прямой линией [3].

Линейная зависимость между переменными x и y описывается уравнением общего вида , где a, b, c, d, … – параметры уравнения, определяющие соотношения между аргументами x₁, x₂, x₃, …, x_m и функций .

 

В практике учитывают не все возможные, а лишь некоторые аргументы, в простейшем случае – всего один, представленный на формуле (2):

 

(2)

 

В уравнении линейной регрессии (2) a – свободный член, а параметр b определяет наклон линии регрессии по отношению к осям прямоугольных координат. В аналитической геометрии этот параметр называют угловым коэффициентом, а в биометрии – коэффициентом регрессии. Наглядное представление об этом параметре и о положении линий регрессии Y по X и X по Y в системе прямоугольных координат дает рис.1.

 

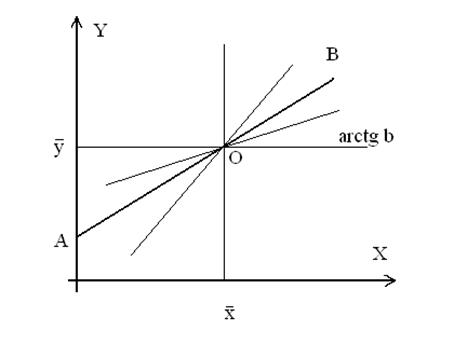
Рис. 1- Линии регрессии Y по X и X по Y в системе

прямоугольных координат

 

Линии регрессии, как показано на рис.1, пересекаются в точке О (, ), соответствующей средним арифметическим значениям корреляционно связанных друг с другом признаков Y и X. При построении графиков регрессии по оси абсцисс откладывают значения независимой переменной X, а по оси ординат – значения зависимой переменной, или функции Y. Линия АВ, проходящая через точку О (, ) соответствует полной (функциональной) зависимости между переменными величинами Y и X, когда коэффициент корреляции 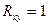. Чем сильнее связь между Y и X, тем ближе линии регрессии к АВ, и, наоборот, чем слабее связь между этими величинами, тем более удаленными оказываются линии регрессии от АВ. При отсутствии связи между признаками линии регрессии оказываются под прямым углом по отношению друг к другу и .

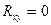Поскольку показатели регрессии выражают корреляционную связь двусторонне, уравнение регрессии (2) следует записывать так:

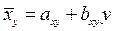и (3)

 

По первой формуле определяют усредненные значения при изменении признака X на единицу меры, по второй – усредненные значения 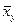при изменении на единицу меры признака Y [4].

Коэффициент регрессии. Коэффициент регрессии показывает, насколько в среднем величина одного признака y изменяется при изменении на единицу меры другого, корреляционно связанного с Y признака X. Этот показатель определяют по формуле (4):

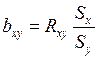или (4)

 

Здесь значения s умножают на размеры классовых интервалов λ, если их находили по вариационным рядам или корреляционным таблицам.

Коэффициент регрессии можно вычислить, минуя расчет средних квадратичных отклонений s_y и s_x по формуле (4):

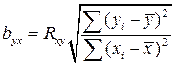или (5)

 

Если же коэффициент корреляции неизвестен, коэффициент регрессии определяют следующим образом:

 

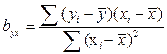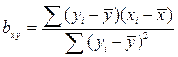или . (6)

 

Связь между коэффициентами регрессии и корреляции. Эта связь выражается равенством 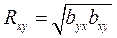(7):

(7)

 

Таким образом, коэффициент корреляции равен средней геометрической из коэффициентов b_yx и b_xy. Формула (7) позволяет, во-первых, по известным значениям коэффициентов регрессии b_yx и b_xy определять коэффициент регрессии R_xy, а во-вторых, проверять правильность расчета этого показателя корреляционной связи R_xy между варьирующими признаками X и Y.

Как и коэффициент корреляции, коэффициент регрессии характеризует только линейную связь и сопровождается знаком плюс при положительной и знаком минус при отрицательной связи.

Определение параметров линейной регрессии. Известно, что сумма квадратов отклонений вариант x_i от средней 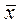есть величина наименьшая, т.е. . Эта теорема составляет основу метода наименьших квадратов. В отношении линейной регрессии [см. формулу (2)] требованию этой теоремы удовлетворяет некоторая система уравнений, называемых нормальными:

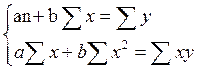
Совместное решение этих уравнений относительно параметров a и b приводит к следующим результатам:

 

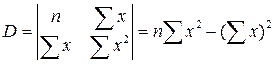
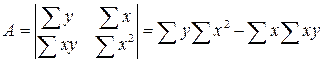
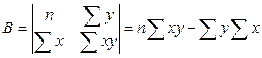, откуда и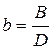

 

Учитывая двусторонний характер связи между переменными Y и X, формулу для определения параметра, а следует выразить так:

(8)

 

Параметр b, или коэффициент регрессии, определяют по следующим формулам:

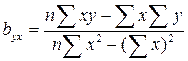(9)

 

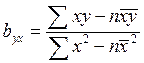(10)