В эпитаксиальных гетеронаноструктурах очень важно обеспечить согласование параметров решеток осаждаемого слоя и подложки, что является необходимым условием для формирования качественной кристаллической структуры слоев и границ между ними. Эта задача решается использованием твердых растворов AIIIBV, наибольшее распространение среди которых сегодня получили AlGaAs и InGaAs.
Рассматриваемые твердые растворы InxGa1-xA и AlxGa1-xAs образованы соединениями GaAs, InAs и AlAs, исходные параметры которых приведены в таблице 1.
Таблица 1
| Параметр | GaAs | AlAs | InAs |
| Постоянная решетки a, А | 5,653 | 5,661 | 6,058 |
| Ширина запрещенной зоны Eg, эВ | 1,424 | 2,153 | 0,354 |
| ТКР α, 1/ºК | 5,73·10-6 | 5,20·10-6 | 4,52·10-6 |
| Упругие постоянные, Г Па С11 С12 С44 | 119,0 53,4 59,6 | 125,0 53,4 54,2 | 83,4 45,4 39,5 |
| Модули Юнга Е, ГПа | 85,9 | 83,5 | 51,4 |
| Межзонный гидростатический потенциал А, эВ | -7,0 | -6,3 | -6,0 |
| Сдвиговый деформационный потенциал B, эВ | -1,7 | -1,5 | -1,8 |
Вследствие изоморфизма кристаллического строения твердых растворов период решетки а(х) твердого раствора вида AxB1-xC подчиняется правилу Вегарда, т.е. линейно зависит от состава х и периодов решетки входящих в него соединений:
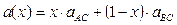
| (1) |
Аналогично, в первом приближении, можно выразить большинство параметров тройных соединений (четырехкомпонентные растворы не рассматриваются). Тогда имеем для ширины запрещенной зоны:
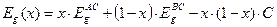
| (2) |
где С – параметр квадратичной нелинейности (провисания) раствора. Для AlxGa1-xAs С = 0,143, а для InxGa1-xAs – С = 0,430.
Разрывы до зоны проводимости и потолка валентной зоны на гетерогранице в системе InxGa1-xAs /GaAs можно оценить по эмпирическим формулам:
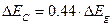
| (3) |
Для AlxGa1-xAs использование выражения (2) для вычисления ширины запрещенной зоны некорректно, т.к. AlAs – непрямозонный полупроводник, в отличие от GaAs и InAs. Это приводит к тому, что при определенном содержании AlAs (x = 0,41…0,45) раствор также становится непрямозонным. Зависимость Eg(x) для этого соединения была получена экспериментально и имеет вид:
| (4) |
Разрывы энергетических зон на границе AlxGa1-xAs/GaAs рассчитываются по формулам:
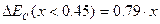
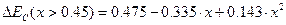
| (5) |
Для температурных коэффициентов расширения, согласно правилу Вегарда, получим выражение вида:
| (6) |
для упругих постоянных:
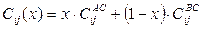
| (7) |
для модулей Юнга:
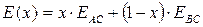
| (8) |
для коэффициентов Пуассона:
| (9) |
и для межзонного гидростатического и сдвигового деформационных потенциалов:
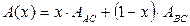
| (10) |
| (11) |
В случае плосконапряженного псевдоморфного слоя кубического кристалла (все образующие раствор соединения имеют структуру цинковой обманки) и плоскости подложки (001) тензор деформации εij – диагональный и его компоненты связаны между собой соотношениями:
| (12) |
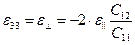
| (13) |
где ε|| и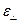 
– параллельная и перпендикулярная компоненты относительной деформации решетки.
Вычисление параллельной компоненты относительной деформации позволяет провести оценку влияния упругих напряжений на ширину запрещенной зоны через гидростатический и сдвиговый деформационные потенциалы:
| (14) |
где
| (15) |
– компонента энергии деформации, обусловленная сжатием кристаллической решетки в плоскости слоя (по направлениям x и y), а
| (16) |
– компонента энергии деформации, обусловленная растяжением кристаллической решетки в направлении, перпендикулярном плоскости слоя (вдоль оси z).
Упругие напряжения, возникающие из-за рассогласования параметров решеток слоя и подложки, могут быть оценены из соотношения:
| (17) |
Критическая толщина эпитаксиального слоя определяется из выражения:
| (18) |
Компонента остаточных напряжений, вызванная рассогласованием материалов по ТКР, рассчитывается по формуле:
| (19) |
где
| (20) |
– относительная деформация, вносимая разностью ТКР слоя и подложки (ΔT – разность температур осаждения и комнатной),
| (21) |
– эффективный модуль Юнга.
Тогда остаточные напряжения, возникающие в эпитаксиальном слое, вычисляются по формуле:
| (22) |
