Расчеты цепей переменного тока проводят не для мгновенных, а для действующих значений токов и напряжений, которые в дальнейшем будем называть ток и напряжение.
Для цепи переменного тока справедливо положение (3). При этом создаваемые током падения напряжений UR = IR и Ul = IXl совместно противодействуют напряжению источника.
Если бы UR и UL совпадали по фазе, то U=UR+Ul = 140 В. Докажем, что они не совпадают по фазе, при помощи векторной диаграммы (рис. 4.21). Построение диаграммы начинаем с вектора тока, так как он одинаков для обоих участков.

|
К нему пристраиваем вектор UR, совпадающий по фазе с током на активном сопротивлении (см. рис. 4.10), и вектор UL, опережающий ток по фазе на 90° на индуктивном сопротивлении (см. рис.4.18). Получаем, что векторы UR и UL сдвинуты между собой по фазе на 90°. Складывая их, находим результирующее напряжение цепи:
U=√U2R+ U2 L (4.9)
В цепи, имеющей, кроме индуктивного, активное сопротивление, напряжение опережает ток на угол, значение которого меньше, чем 90° (1).
Из уравнения (4.9) U=√I2 R2 + √I2 X2 L = I√R2 + √X2 L = IZ,
где Z – полное сопротивление цепи:
Z = √R 2 + X2 L; (4.10)
 I=U/Z. (4.11)
I=U/Z. (4.11)
Формула (4.11) отражает закон Ома, а (4.10) позволяет вычислять полное сопротивление цепи. Разделив стороны треугольника напряжений (выраженные в единицах напряжения) (рис. 4.21) на ток, получаем треугольник сопротивлений (рис. 4.22), из которого
R= Z cos φ; XL = Z sin φ. (4.12)
Активная мощность рассматриваемой цепи P = I2R, реактивная
Ql = I2Xl. Полная мощность цепи S = I2Z.

Умножив стороны треугольника напряжений (выраженные в единицах напряжения) на ток, получаем треугольник мощностей (рис. 4.23), из которого
 S = UI, S =√P2 + Q2L ; (4.13)
S = UI, S =√P2 + Q2L ; (4.13)
P = S cosφ = UI cosφ; (4.14)
Q = S sin φ == UI sin φ. (4.15)
За единицу активной мощности принят ватт (Вт), реактивной — вольт-ампер реактивный (вар), полной — вольт-ампер (В • А).

Из формул (4.12), (4.15) можно определить cosφ или sinφ, азатем угол φ, который является углом сдвига фаз между током и напряжением. Этот угол можно также найти из рис.4.21, 4.22, 4.23. Во всех треугольниках он одинаковый, так как треугольники подобные.
ЦЕПЬ ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
АКТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО
СОПРОТИВЛЕНИЙ
В цепи (рис. 4.24) создаваемые током падения напряжений UR = IR, UL = IXL, Uс = 1ХС противодействуют напряжению источника U. Совместное противодействие UL и Uс называют реактивным напряжением Up.
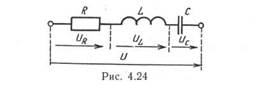
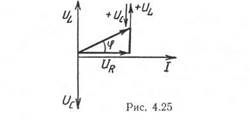
Из векторной диаграммы (рис. 4.25), на которой UL опережает ток, a Uc отстает от тока по фазе на 90°, наглядно видно, что при последовательном соединении индуктивности и емкости напряжения на них находятся в противофазе (1).
Умножив стороны треугольника напряжений (выраженные в единицах напряжения) на ток, получаем треугольник мощностей
(рис. 4.26).из которого Q = QL — QC и
S= √ P 2 + √(QL - Q C) 2 (4.16)
Реактивная мощность цепи равна разности индуктивной и емкостной мощностей (2).

Разделив стороны треугольника напряжений (выраженные в единицах напряжения) на ток, получаем треугольник сопротивлений (рис. 4.27), из которого Х = XL – XC

Реактивное сопротивление цепи равно разности индуктивного и емкостного сопротивлений (3).
Почему же берется не сумма, а разность между реактивными сопротивлениями XL и Xс и мощностями Ql и Qc? Это можно объяснить тем, что между катушкой и конденсатором происходит обмен энергиями, при котором мгновенные значения ЭДС самоиндукции eL катушки (обусловливающей XL и Ql) и напряжения конденсатора иC (обусловливающего Хс и Qc) в любой момент времени направлены навстречу друг другу (рис. 4.28). Так, в момент, когда конденсатор заряжается (рис. 4.28,а), возрастающее напряжение конденсатора иС

|
направлено противоположно току (мешая зарядке), и ток уменьшается (при полной зарядке конденсатора он станет равным нулю). Уменьшение тока вызывает ЭДС самоиндукции еL в катушке, которая стремится, по закону Ленца, увеличить ток. В результате иС и еL направлены навстречу другу и энергия магнитного поля катушки посредством ЭДС eL преобразуется в энергию конденсатора. При разрядке конденсатора все происходит наоборот (рис. 4.28, б): уменьшающееся напряжение конденсатора ис совпадает по направлению с током, увеличивая его, а возрастающий ток наводит eLy направленную, по правилу Ленца, противоположно току. В результате ис и eL направлены навстречу друг другу и энергия конденсатора идет на создание магнитного поля катушки.
Если бы в схеме не было емкости, напряжение на катушке было бы равно напряжению источника при
 токе I=U/√R2 + X2L.
токе I=U/√R2 + X2L.
За счет емкости можно уменьшить реактивное сопротивление цепи
X = XL — Хс, что увеличит ток, а значит, и падение напряжения
UL =IXL. Напряжение на катушке можно увеличить, подключив последовательно с ней конденсатор (4). Самое большое напряжение на катушке при XL=XC.
В зависимости от соотношения XL и Хс возможны три режима работы цепи (рис. 4.29): а) напряжение цепи опережает ток по фазе на
угол φ (который считают положительным) и цепь в целом имеет

|
имеет активно-индуктивный характер; б) напряжение цепи отстает по фазе от тока на угол φ (который считают отрицательным) и цепь в целом имеет активно-емкостный характер; в) напряжение и ток цепи совпадают по фазе, характер цепи в целом чисто активный. Последний режим цепи называется резонансом напряжений, при котором UL = UC, XL = Хс. Настроить цепь в резонанс напряжений можно путем изменения Хс или XL, т. е. изменяя С, L или f.
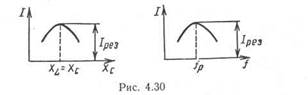
Реактивное сопротивление цепи при резонансе напряжений
X = XL — Хс = 0, поэтому ток I рез = U/ √R2 + √ (XL — Хс)2 = U/R максимальный (рис. 4.30).
Так как при резонансе напряжений XL = Хс, т.е. 2πfL = 1/(2πf С), то частота, при которой наступает резонанс.

Явление резонанса в электрических цепях нашло широкое применение в электротехнике, радиотехнике и электронике. Так, в радиотехнике резонанс — почти единственный путь, позволяющий отделить сигналы
радиостанции от всех остальных сигналов (при помощи резонансного усилителя). Кроме того, используются: резонансное реле — в схемах автоматического управления, резонансный мост — при измерениях R, L и С, резонансный трансформатор — в рентгеновских аппаратах и т. д.
Однако при определенных условиях резонансные явления в электрических цепях могут оказаться вредными, способными разрушить электроустановку. Так, появление в цепи не предусмотренного расчетами резонанса напряжений приводит, в соответствии с положением (4) данного параграфа, к перенапряжениям в элементах цепи, а отсюда может возникнуть пробой электроизоляции установки.






