Математикалық есептер шешуде анализ бен синтез кең түрде қолданылады. Анализ – ізделіндіден берілгенге қарай көше отырып талқылау жолы. Синтез – берілгеннен бастап ізделіндіге көшу (өту) жолы. Бұл екі методта бір-бірімен тығыз байланыста болады.
1) дәлелдеуге берілген есептерді шешудегі анализ бен синтез.
Мысалы,Шар үшбұрышты пирамиданың барлық бүйір жақтарын олардың биссектрисаларының қиылысу нүктесінде жанайды. Дұрыс пирамида екенін дәлелдеңдер.
Анализ. Пирамиданың дұрыс екенін дәлелдеу үшін оның табаны дұрыс үшбұрыш екенін көрсету қажет. (DАВС). Ал бүйір жақтары тең бүйірлі тең үшбұрыштар болуы керек. Бірінші сөйлемді дәлелдеу үшін АС=AB=BC көрсету керек, бұл өз кезінде DАВС=DАSВ=DВSС болуы қажетті. Бұл қатыстарды дәлелдеу үшін үшбұрыштың теңдік белгілерін пайдаланамыз. (пирамиданың бүйір қабырғалары). (Пирамиданың қабырғалары және оған іргелес жатқан екі бұрышы бойынша).
Шар бұл бүйір жақтарды жанау үшін DO1SC=DO2SC және DO2BS=DO3BS. (шеңбердің бір нүктесіне жүргізілген жанаманың кесінділері).
O1S=O2S=O3S, O1C=O2C, O2B=O3B (бір нүктеден жүргізілген жанамалар).
2) Анализ орындалуы. Егер келесі әрбір сөйлемнің жеткіліктілігін тағайындай алсақ, онда дәлелдеу орынды деуге болады.
Синтез. O1, O2 нүктелері DАSВ және DSВС –на сәйкес биссектрисалардың қиылысу нүктелері.
(SDE) жазықтығы берілген шармен белгілі бір дөңгелек бойынша қиылысады. Дәл осы сияқты (СО1О2) жазықтығы берілген шарды басқа дөңгелек бойымен қиылысады.
Мәселе есептердегі анализбен синтездің қолданылуы.
Мәселе есеп тек математикалық фактілермен бірге басқа да сюжеттен тұрады. Мәтінді есеп құрғанда анализ арқылы арифметикалық аппарат көмегімен есептің жоспарын құруға келеміз. Ал есеп көбінесе синтетикалық методпен шешіледі.
3) Мәселе есептер шешуде анализбен синтезді қолдану.
Мәселе есеп деп бұл арада берілгендері тек математикалық мазмұннан тұрмай сонымен бірге басқа да сюжеттен тұратын есептерді айтады. Мәтінді есеп құрғанда анализ арқылы арифметикалық аппарат көмегімен есепті шешу жоспарын құрамыз. Ал есеп көбінесе синтетикалық методпен шешіледі.
Мысалы,Үйдің үлкен бөлмесінің ені 4м, ұзындығы 
ал кішкене бөлменің ұзындығы 4м, ені 
Бір бөлменің ауданы екіншісінен қанша артық?
Анализ. Сұраққа жауап беру үшін бөлмелердің аудандарының және олардың айырмасын табу керек. Бөлмелердің аудандары оның ұзындығы мен енін көбейткенге тең.
Есептің жоспары: әрбір бөлменің ауданын тауып үлкенінен кішісін алу керек.
Синтез. 1-тәсіл 1) Үлкен бөлменің ауданы қандай?
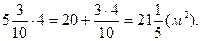
2) Кіші бөлменің ауданы қандай?
3) Бірінші бөлменің ауданы екіншісінен қанша артық?
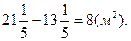
2-тәсіл. Үлкен бөлме ауданы 
екіншісі 
бұлардың айырмасы 
2-тәсіл, синтетикалық әдіс ұтымды, бұған көбейтудің үлестірімділік заңы қолданылады.
Алгебраның есептері (теңдеулер құруға берілген есептер, теңдеулер мен олардың ситемасы, теңсіздіктер мен олардың системасы) тек анализ не тек синтез қолданылып шешіледі. Теңдеулер құрғанда алдымен белгісізден берілгенге ауысады, яғни анализ қолданылады. Теңдеулер не теңдеулер жүйесі синтез әдісі бойынша шешіледі.
Мысалы, Теплоход өзен ағысы бойынша 13 сағатта қанша км жүзсе, ол өзен ағысына қарсы 15 сағатта сондай қашықтыққа жүзді. Егер теплоходтың меншікті жылдамдығы 70км/сағ болса, онда өзен ағысының жылдамдығы қандай?
Анализ. Өзен ағысының жылдамдығын табу үшін теплоходтың меншікті жылдамдығын (70 км/сағ) және өзен ағысы не ағысқа қарсы қозғалыс жылдамдығын білу жеткілікті. Егер өзен ағысының жылдамдығы V км/сағ болса, онда теплоход өзен ағысы бойынша (70+V), ағысқа қарсы (70-V) км/сағ жылдамдықпен жүзеді. Жүрілген жолды уақытқа қатысты теңдеу ретінде өрнектейміз, яғни өзен ағысы және ағысқа қарсы жүрілген жолдардағы арақашықтықтарды теңдестіреміз.
Синтез. 15(70-V)=13(70+V) Û15· 70 -15V=13·70+13VÛ екі жағын 28¹0 ге бөлу. 28V=(15-13)70Û28V=2·70 ÛV=5.
Математикалық анализдің ең үлкен, ең кіші мәнін табуға берілген есептерде анализ, синтез қолданылады.
3) Геометриялық салу есептерін шешкендегі анализбен синтез.
Конструктивтік есептерді немесе геометриялық салу есептерін шешу барысы анализ бен синтезге тіреледі. Бұл есептер анализ, салу, дәлелдеу, зерттеу сияқты кезеңдерден тұрады. Мұндай есептер анализ жасаудан басталады. Бұл шынында да анализ әдісі - өйткені ізделініп отырған элементтен басталып («ізделінді фигура салынды деп ұйғаралық») берілгенге көшеді. Анализ жасау кезеңінде есепті салу жоспары жасалады, одан соң синтетикалық жолмен орындалады. Дәлелдеу кезеңінде анализ бен синтез бірге қолданылады. Зерттеу анализ әдісінің қаншалықты тиімді қолданылғанын байқайды.
Мысалы, а түзуі және оған қатысты симметриялы А, А1 нүктелері және В нүктесі берілген. а түзуіне қатысты алғанда В нүктесіне симметриялы В1 нүктесін бір сызғыштың көмегімен салу керек.
Анализ. Есеп шешілді, ізделінді нүкте салынды деп ұйғаралық, яғни В1=Sa(B). Есеп шарты бойынша А1=Sa(A). В1 – нүктесін салу үшін осы нүкте қиылысатын екі түзу салу керек. Бұл түзулерді былайша таңдап алуға болады: А1В1=Sa(AB), B1=Sa(A1B), A1B1 ÇAB1=B1.
Бұл түзулерді салу үшін АВ мен а түзулерінің қиылысу нүктесін (С1-нүктесі) және А1В мен а түзулерінің (С2-нүктесі) қиылысу нүктелерін салу керек. Енді А1С1ÇАС1=B1. Есепті салу жоспары жасалды. Барлық салу бір ғана сызғышпен орындалады.
Салу (синтез). Сызғыштың көмегімен А1В және АВ тузулерін салып С1С2 нүктелерін табамыз, АС2 және А1С1 түзулерін саламыз, бұлардың қиылысу нүктесі – В1.
Дәлелдеу (синтез). А1С1=Sa(AC1), AC2= Sa(A1C2), AC1Ç A1C2=B, B1= А1С1Ç AC2, сондықтан B1= Sa(В).
(а түзуіне симметриялы екі түзудің қиылысу нүктесі ретінде)
Зерттеу (анализ). АВ мен а түзуінің бір ғана ортақ нүктесі бар. АВ мен а-ның тағы қандай орналасуы бар? Бұлар бір жазықтықта жатыр, сондықтан олар бір ортақ нүктесі не параллель болуы мүмкін. Егер олар параллель болса, жоғарыдағы салулар орындалмайды. АВççа және АВ¹а. Есеп бір КÏА алып. К1=Sa(K), берілген А1= Sa(A), бұдан соң есеп К, К1 және В бірінші жағдайға келеді.
Егер В нүктесі а түзуінде жатса, онда есеп В= Sa(B).
Мысалы, Берілген а түзуі арқылы берілген b түзуіне параллель жазықтық жүргізу керек.
Анализ. 
жазықтығын салу үшін аÎ 
және bçç 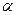- бұл жазықтық а арқылы өтіп b-ға параллель болуы керек. Яғни 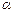(а,с) және сççb.
Салу. Берілген а түзуінің бойынан " А нүктесін аламыз.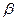 
(А,В) жазықтығында сççb, аÇс=А саламыз. 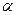(а,с) – салуға тиісті жазықтық.
Дәлелдеу. сççb және сÌ 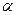, сондықтан 
ççb. Бірақ аÌс.
Зерттеу. Салу жұмысы кеңістікте екі а,в түзулердің кеңістікте орналасуына байланысты үш жағдай болуы мүмкін.
1) а және b түзулері (а-b) айқас болуы мүмкін. Бұл жағдайда есептің бір шешімі болады. Қандай болса да АÎа; сÇа=А және сççb болатын жалғыз ғана с түзуі болады. Мұндай түзулердің жиыны жазықтықтың біреу ғана сÌ 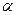және ççb қасиетке ие болатынын анықтайды.
2) аççb. А түзуі арқылы өтетін " жазықтық есеп шартын қанағаттандырады.
3) аÇb=А. Есептің бір шешімі бар 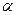(а,в).
 |
Мысалы, Табанының ұзындығы а, биіктігі һа тең бүйірлі үшбұрышты салу керек.
Анализ. Есеп шешілді, берілген а, һа бойынша үшбұрыш салынды деп ұйғаралық.
А
| ||||||
|
| |||||
| ||||||
Һа – биіктігі АВС тең бүйірлі үшбұрышты тең екі тікбұрышты үшбұрышқа бөледі. Сондықтан есеп берілген һа және катеттері бойынша АDB тік бұрышты үшбұрышты салуға келтіріледі.
Салу. Берілген һа және бойынша DADB-ны саламыз, ВD-ның D нүктесінен DC=DB болатындай С нүктесін табамыз, С - D-тың үшінші төбесі, оны А мен қосамыз.
DABС шығады.
Дәлелдеу. Салынған D- іздеп салуға тиісті үшбұрыш, ол есеп шартын қанағаттандырады. Біріншіден тең бүйірлі, АВ=АС, табаны ВС=а және биіктігі AD=ha.
Зерттеу. Есеп ADB тікбұрышты D-ты салуға (һа, ) келеді, бұл әрқашан мүмкін, оның бір шешімі болады.
4.2. Есептер шешудің басқа да жалпы әдістері.
Жоғарыда қарастырылған пінкттердегі анализ бен синтез есептер шешудің барынша жалпы әдісі болып табылады. Төменде қарастырылатын әдістерде жалпы әдістер болып саналады.
а) Жеткілікті түрде сынау әдісі.
Есеп шартын қанағаттандыратын барлық логикалық мүмкіндіктер және оларды таңдап алу. Егер есеп шартына сай логикалық мүмкіндіктер шектеулі сандар болса, онда есеп шартына толық сай келетін әдісті сұрыптап алу. Осы әдіспен кейбір сандар теориясының есептері шешіледі.
Мысалы, Цифрларының қосындысы çç, өзі çç-ге бөлінетін барлық төрт таңбалы сандарды табыңдар.
Шешуі. Ізделінетін сан fbcd=103a+102b+10c+d болсын. Есеп шартына сүйеніп жүйені жазуға болады.
Осы жүйенің екінші теңдеуі ізделетін санның параллельге бөлінетінін білдіреді.
Бір-біріне қоссақ 2(а-с)=11(k+1). Мұндағы kÎ(-1;0;1) болады. Шынында да жүйенің екінші теңдеуінде сол жағының айырмасы 11-ден кіші, çç - деп үлкен болмауы керек.
б) Екінші әдіс. – мәліметтер әдісі.
|
Мысалы, х2-2ху+у2-2х+3>0.
Шешуі. х2-2ху+у2-2х+3=х2-2х(у+1)+(у+1)2-(у+1)2+2у2+3=(x-y-1)2+y2-2y+1+1=(x-y-1)2+(y-1)2+1>0.
Мәліметтерді қабылдаудың негізіне геометриялық салу есептерін шешу жатады. Осы түрдегі әрбір есеп мынадый талаптардан тұрады: берілген фигура арқылы, оның конструктивті элементтері арқылы фигура салады, ол есеп шартын қанағаттандыруы керек. Салынуға тиісті есеп элементар салуларға келеді. Мәліметтер әдісімен текстілі есептер арифметикалық тәсілмен шешіледі. Бұл арада да берілген есеп жай есепке келтіріледі.
в) Есептер шешудің үшінші әдісі: модельдеуге негізделеді.
Модельдеуге әртүрлі математикалық объектілер пайдаланылады. Сан формулалар, сан таблицалары, әріпті формулалар, функциялар, алгебралық теңдеулер, дифференциалды теңдеулер мен олардың жүйелері, теңсіздіктер, теңсіздіктер жүйесі, қатарлар, геометриялық фигуралар, әр алуан граф, схемалар, Венн диаграммалары, т.б. Математикалық модельдеу көптеген текстілі есептер шешуде қолданылады. Есеп шарты бойынша құрылған теңдеу – алгебралық (аналитикалық) модель болып табылады.
Берілген геометриялық есептегі фигураның сызбасы – ондағы берілгендер мен ізделетін айнымалылар да – геометриялық модель болады. Көлемді геометриялық фигура – есепте берілген заттарды кескіндеу не оны қолдану моделі болады.
Мысалы, Егер сыныптағы оқушыға 2-ден конфет таратылса, онда 17 конфет артылады. Егер 3 конфеттен таратылса, онда 2 оқушыға конфет жетпейді. Сыныпта неше оқушы, неше конфет?
Бұл есепті 2 сызықтық теңдеу құру арқылы шешуге болады. Егер бұған модуль құрсақ, онда бұл есепті бастауыш сынып оқушылары шеше алады.
2 2 2... 2 22+17
€ € €... € €€
3 3 3... 3
Модельден байқалатындай: 2 конфет алған оқушы 3 конфет алуы үшін 17 конфетті және 4 конфетті тарату керек. Өйткені 2 оқушыға конфет жетпей қалған. Яғни қосымша 21 конфет тарату керек. Демек, сыныпта 23 оқушы. А, конфет 21 
3=63.
Орта мекетеп математикасында графиктік модельдеу ерекше роль атқарады: диаграммалар, функциялық графигі, теңдеудің, теңсіздіктің, графиктің геометриялық мағынасы.
Мысалы, Екіншілер бригадасы бірі екіншісінен 2 еседен көбірек шабындықты шабу керек. Олар жарты күнде үлкен шабындықта болды. Түстен кейін бригаданың жартысы үлкен шабындықта қалды да кешке дейін оны ақырына дейін шауып бітірді. Бригаданың екінші жартысы түстен кейін кіші шабындықта болды. Олар толық шауып бітіре алмады. Шабылмай қалған жерді келесі күні 1 шалғышы шауып бітірді. Бригадада неше шалғышы бар? Барлық шалғышылардың бір күнде шабатын жер мөлшері бірдей.
Шешуі. Шалғышылар саны – х; 0,5x
Есеп шарты диаграммада көрсетілген.
0,5х+2=0,5 1,5x x 0,5x
x=8
г) Ізделетін шаманың мәнін біртіндеп жуықтап есептеу әдісі.
Есептерді графиктік тәсілмен шешудің бәрі жуық түрде есептеледі. Жуықтап шешу сандар методы (мысалы, квадрат теңдеудің түбірлерінің шешімі формула бойынша табылады).
Геометрияда жуықтап салу методы бар.
Мысалы, дөңгелекке тең квадрат салу бұрышты тең бөліктерге бөлу, т.б. Практикалық мазмұнды есептер көбінесе комбициялық методтармен шешіледі. Орта мектепте есептер шешудің негізгі мақсаттарының бірі - әр оқушының математикалық есептердің негізгі методтар мен есеп шешудің тәсілдерін меңгеруін қамтамасыз ету.
4.3. есептер шешу кезінде мұғалімнің оқушыларға беретін жалпы нұсқаулары.
1) Есептің қойылысы және оның мазмұнын меңгеру үшін беретін ұсыныстар (1-этап).
2) Есеп шешу жоспарын құру (2-этап).
3) Есепті шешу жоспарын іске асыру (2-3 этап).
4) Есеп шешімінің дұрыстығына талдау жасап тексеру (4-этап).
5) Жалпы нұсқаулардан дербес нұсқауларға.
6) Айтылған нұсқауларды есептер шешуге қолдану.
Есептер шешуді үйрену үшін оларды шешу туралы тәжірибе жинақтау керек. Есептер шешу дағдысын өзбетімен қалыптастыратын оқушылар өте сирек кездеседі. Есептер шешу дағдысына оқушыларды үйрету мұғалімнің міндеті. Егер мұғалім үйренуге тиістінің бәрін өз міндетіне алып, оқушыға өте көп көмектессе, оқушыны ойландыратын ешнәрсе қалмаса (яғни оқушы ойланып тәжірибе жинақтауға қажетті өте аз материал қалса), онда оқушы есеп шығаруды үйренбейді. Егер мұғалімнің есеп шығарушыға көмегі өте аз болса да ол жағдайда оқушы есеп шығаруды үйрене алмайды. Мұғалім оқушыға есепті қалай шығару жөнінде ақыл-кеңес беріп көмектесуі немесе оқушы есепті дұрыс шығара алатындай болуы үшін олардың сұрақтарына жауап беруі керек. Кейде мұғалім есеп шығару үшін өзі сұрақ қойып, оған өзі жауап береді. Біріншіден оқушылар бұған еліктейді, есеп шығара бастайды. Оқытудың мұндай түрі көп уақыт жұмсауды қажетсінеді, әрқашан табысқа жете бермейді.
Бұл арада оқушының ойын тудыратын, ойлау қызметін дамытатындай творчестволық тәсіл керек.
Мұндай ақыл-кеңестер әртүрлі есептер шешуге жарайтын жалпылық қасиеті болуы керек. «Есептер шешу дегеніміз практикадан қалыптасатын өнер», дейді Д.Пойа.
Оқушыларға айтылатын ақыл кеңестермен сұрақтарды шартты түрде 4 топқа бөлуге болады. Бұл топтар бір-бірімен қатаң бөлінбеген, есептер шешу кезінде бұлардың арасында белгілі байланыс болады.
1) Есептің мазмұнын меңгеру үшін қойылатын сұрақтар мен ақыл кеңестер (1-этап).
Есептің берілгендері қандай, нелер ізделеді, немен қорытындыланады – бұларды білмей тұрып есеп шешуге кіріспейді.
«Есепті шешуге асықпаңыз» - бұл есеп шешуге дайындық жасау керек деген сөз, бұл
а) есеппен таныс, мазмұнын оқы, есептегі жалпы жағдайды еске сақта;
б) берілгендер мен есептің сұрайтынын біліңдер. Дәлелдеу есебінде алғашқы шарт (қолайлы жағдаймен) пен қорытындыны бөл.
Мысалы, ұзындықтары а,в болатын тік бүрышты үшбұрыш үшін гипотенузаны табанын формуланы қорытыңдар.
Берілгендері үшбұрыш, оның а,в катеттері, сұрайтыны оның гипотенузасын табатын формула болып табылады.
в) Егер есеп геометриялық есеп болса, онда оның сызбасын сал, сызбада берілгендер мен ізделетін шамаларды белгіле.
г) Есеп шартында белгілеулер жоқ болса, оған қолайлы белгілеулер ендір. Мысалы, үшбұрыш а,в,с. R, а+в-с=2r.
д) Есептің мазмұнын түсіне бастаған кезде «Есептің шартын қанағаттандыра ма?» деген сұраққа жауап беру қолайлы. Есептің мағынасы бола ма, қандай жай түрлендіруден соң ең жеңіл түрге келе ме?
2) Есепті шешу жоспарын құру (2-этап).
Есепті шешу жолдарын құру – есеп шешудегі ең негізгі қадам. Дұрыс құрылған жоспар есептің дұрыс шешіміне кепілдік береді. Жоспар құру күрделі және ұзақ процесс болуы мүмкін. Соның оның шешімін табатындай «жаңашыл» меңгерту керек.
а) Осы есепке ұқсас есеп сізге белгілі ме? Осы есепке мағынасы жөнінен жақын есеп сізге таныс па? Егер бұл есептер сізге бұрыннан таныс болса, онда жоспар құру қиынға соқпайды. Мысалы, шар радиусын оны іштей сызылған тік параллелепипедтің диагоналы арқылы өрнекте деген есепке ұқсас, шеңбер радиусын оған іштей сызылған төртбұрыш диаметрімен өрнекте десек, бұлар туыстас. Бұл әрқашан табыла бермейді.
б) шешуге тиісті есептке келтірілетін есеп құрастыр – сіз бұған бұрын жоспар құрғансыз.
в) шешуге тиісті есепке мағыналас есеп сізге белгісіз, ендеше жоспар бірден құрылмайды. «есепті басқаша тұжырымдаңыз», мұның математикалық мазмұны өзгермейтін болсын.
Мысалы, "n үшін n2-n өрнегінің мәні жұп екенін дәлелдеңдер. Мұны басқаша тұжырымдалық: «Өрнектікөбейткіштерге жіктеңдер, ең болмағанда бір көбейткіш 2-ге бөлінетін болсын». Бұған математикалық ұғым не бөлінгіштік белгі қолданылады. Есеп мазмұнын математикаландыру – теңдеулер құруда көп қолданылады.
г) Есепті шешу жоспарын құру барысында есеп шешуші – «Есептің берілгендері түгел қолданылды ма?» деген сұрақ қояды.
д) есепті шешу жоспарын құру барысында «Есептің берілгендерін немесе есептің сұрайтынын түрлендіріп көріңіз». Ізделіндімен берілгендерді түрлендіру жоспарды тезірек құруға көмектеседі. Ізделіндіні түрлендіріп берілгенге жақындатады және керісінше әр нақты жағдайда берілгендерді теңбе-тең түрлендіріп біртіндеп нәтижеге ізделіндіге жақындаймыз. Теңдеу, теңсіздік, не олардың жүйесінің шешімін табу үшін - өзімен мәндес теңдеулер мен теңсіздіктер арқылы түрленеді.
е) Жоғарыда айтылғандардың бәрін қолданғанда есеп жоспары құрылмайтын жағдайлар жиі кездеседі, онда «Есептің белгілі бір бөлігін шығарып көріңіз» яғни, есептің шартының белгілі бөлігін қанағаттандыратын одан әрі қалған шартты қанағаттандыратын тәсіл іздеңіз.
Мысалы, Берілген үшбұрышқа іштей квадрат салу керек. Квадраттың екі төбесі бір-бірден үшбұрыштың екі қабырғасының бойында, ал қалған екі төбесі 3-қабырғаның бойында жатуы керек.
Ең алдымен есеп шартының бір бөлігін қанағаттандырып көрелік. Үшбұрыш ішіне квадрат саламыз. Квадраттың екі төбесі үшбұрыштың бір қабырғасының бойында, ал үшіншісі – басқа қабырғаның бойында жататын болсын.
Мұндай квадратты өте көп етіп сызуға болады. Барлық квадраттар А төбесіне (центріне) гомотетиялы болады.
Демек, төртінші төбе А нүктесінен және салынған квадраттың төбесінен өтетін түзу және ВС бойында жатуы керек. Есептің жоспары белгілі.
Ақыл-кеңес. «Есептің бір бөлігін шешіп көріңіз» бұдан әрі кеңесімізді кеңейтсек: «Есепті барынша жай есептерге ұсақтаңдар». Мәселе есепті шешудің әр қадамы – арифметикалық тәсілмен шешіледі – ұсақ бөліктерден тұрады. Кейбір геометриялық есептерге теңдеулер жүйесі құрылады.
ж) кейде жоспар құруға «Қандай дербес жағдай үшін осы есепті тез шешуге болады» деген сұрақ көмектеседі. Дербес жағдайдың нәтижесі күрделі жағдайға қолданылады. Біртіндеп жалпылап есепті шешеді. Бұлайша пайымдау – толық индукция әдісі болады.
|
|
Суретте индукция бойынша ойлау схемасы көрсетілген. М үшбұрыштың төбесінде болғанда М-нен екі қабырғасының қашықтығы 0-ге тең. Жалпы жағдайдың бірі – М нүктесінің бір қабырғаның бойында жатуы. MN//АС жүргіземіз. DMNB қосымша тең қабырғалы үшбұрыш аламыз, мұндағы М – төбесі. Соңғы жағдай – М нүктесі DАВС-нің " ішкі нүктесі. А/С///АС жүргізсек, онда есеп алдыңғы жағдайға келеді.
3) Есепті шешу жоспарын іске асыру жоспар – есеп шешімінің жалпы түйінін ашып көрсетеді. Есеп шешімінің жоспарын іске асыруда есептің түйінін сипаттап жазатын барлық ұсақ-түйектерді қарастырылады.
а) «»әрбір қадамыңызды тексеріңіз
әр қадамның дұрыстығын бұған дейін белгілі математикалық фактілер мен сөйлемдерге сүйеніп тексеру керек.
б) Жоспарды іске асыруда «»терминдер мен символдарды олардың анықтамаларымен ауыстыр деген ақыл-кеңес пайдалы.
Мысалы, «Параллелограмм» өзінің «қарама-қарсы қабырғалар қос-қостан» деген анықтама мен ауысады.
в) Объектілер жағдайында берілгендердің қасиетін пайдаланыңдар.
Мысалы, Параллелограммда қарама-қарсы бұрыштары тең болатынын дәлелдеңдер.
Шеші кезінде параллельдігі мен теңдігі қолданылады.
4) Есеп шешімінің дұрыстығын талдау және тексеру.
Есепті жақсы шығаратын оқушының өзі есептің шешу жолын мұқият жазып, «есеп толық шықты» деп есептейді. Мұның дұрыстығы әлі тексерілген жоқ, барынша тиімді вариент таңдап алынған жоқ.
Б.М. Бродис 1) қатесіз, 2) негізделген, 3) аяғына дейін толық шығарылған есеп қана шығарылған есеп болып табылады. Сондықтан есепті талдау, шешімді тексеру нәтижесінің дұрыстығы – есеп шешудің кезеңі болуы керек.
Сонымен «Нәтижесін тексер», «Шешу жолын тексер».
«Осы нәтижені басқаша жолмен алуға бола ма?»
«Есепті басқа тәсілмен шешіңдер».
Бір есепті әртүрлі тәсілмен шешіп тек бір нәтиже алудың зор мәні бар.
Бұл ақыл-кеңестің көпшілігін Д. Пойа тұжырымдады. Бұл ақыл-кеңестер оның шешімін дұрыс іздеуге уақыттан ұтуға, есеп шешудің дұрыс және тиімді тәсілін іздеу ықтималдығы молайады.
5) жалпы ақыл-кеңестерден дербес кеңестерге ауысу.
Есепті жалпы сұрақтардан, жалпы ақыл-кеңестерден бастайды. Жалпы кеңестердің оқушыға әсері аз болуы мүмкін, мұндай жағдайда қосымша мәселелерді, барынша ұсақ сұрақтарды әңгімелейміз. Оқушының математикалық дайындығының деңгейіне қарай біріншіден дербес мәселелерге көшеміз. Барынша ұсақ мәселелер туралы сұрақ қойып оқушы ақыл-ойының есеп шешуге дұрыс бағытталуына әсер ету керек.
.
6) Есеп ұсынылған ақыл-кеңестермен сұрақтарды қолданып мысал есептер шешу.
Есеп. А,В,С
Орманның ауданын табыңдар.
Есеп мазмұнын меңгеру.
1) Мазмұнын талдаймыз.
2) Берілгендерін бөлеміз А,В,С пункттерді (0,5 АВ)2 ВС2, орман 4АС. Орманның ауданы квадрат ауданын 20км2 артық.
Сұрайтыны орманның ауданы, яғни АС-?
3) Есепке чертеж сызу пайдалы.
4) Белгілеулер ендіреміз. АВ=x, BC=y, AC=z.
Бұл есепті меңгеруді ең соңғы қадамы.
Есепке жоспар құру.
Берілгендермен белгісіздер арасында белгілі байланыс орнаттық. Егер бұрын есептей есеп шықпаса, онда 2-ақылды орында.
(1)
Бұл анықталмаған теңдеу, 3 белгісізі бар. Берілгендер толық қолданылды ма? Берілгендер мен ізделінді қалай байланысқан.
не 
.
x, y, z – үшбұрыштың қабырғалары, бұл үшбұрыш жөніндегі аксиоманы қанағаттандырады.
Жоспарды іске асыру.
