Алматы - 2012
Жоспары:
І. Кіріспе
ІІ. Негізгі бөлім
ІІ.1. Есепті қалай шығару керек?
ІІ.2. Минимумдық тәсіл
ІІ.3. Жаңа белгісіз енгізу тәсілі
ІІ.4. Иррационал теңдеуді шығару
ІІ.5. Аралас система тәсілі
ІІ.6. Тригонометриялық теңдеулерді шешу тәсілдері
ІІ.7. Математикалық есептерді шешудің жалпы әдістері.Есептер шешудегі анализ бен синтез.
ІІ.8. Математика есептерін шешуді ұйымдастыру.Есептерді фронтальді шешу.
ІІІ. Қорытынды
Пайдаланылған әдебиеттер тізімі
Кіріспе
Математиканы оқыту методикасынан шығарылатын есептер – негізінен мектептен белгілі, қарастырылуы тиіс оңай есептерге келтіріледі. Оны бірден тану немесе ұқсас есептерге келтіре білу немесе өрнектерді түрлендіру барысында байқау есепті шығаруға мүмкіндік береді. Есеп шығаруда математикалық ұғым анықтамаларын, оның қасиеттерін, қажетті теоремаларды білу, алуан түрлі ережелерді және алгоритмдерді жетік, еркін меңгеру де өз себін тигізері анық. Ол үшін мектептегі математикаға арналған программаның жалпы нұсқаулары мен негізгі білім, білік және дағды көлемдерін басшылыққа алыңыз. Практикада жиі қолданылатын дәрежелеу, толық квадрат бөлу, көбейткіштерге жіктеу, жаңа белгісіз енгізу, орнына қою, бірдей негізге келтіру, салыстыру, потенциалдау, теңдеу құру, қарапайым түрге келтіру, топтау, ортақ көбейткішті жақша сыртына шығару, логарифмдеу, ортақ бөлімге келтіру, симметрия, қосу, азайту, бөлу, көбейту, жекелеу, дәрежені кеміту, графиктік, интегралдау тәсілдерімен қатар, сирек қолданылғанымен есептердің белгілі түрлерін шығаруда көмектесетін аралас система, түйіндестер, аралықтар, түбір табу, мимнимумдық, белгілі коэффициенттер, іріктеу тәсілдерін де меңгеру пайдалы. Бұл тәсілдерге көңіл бөліп, өз бетінше бірнеше мысал қарастыврыңыз. Сонымен сіз мектептік математика курсында айтылатын теориялық мәселелерді толық меңгеріп, есепті шешу тәсілдерін білгеннен кейін есеп шығаруға кірістіңіз делік.
Есепті қалай шығару керек?
Алдымен төмендегі нұсқауларды есіңізде қатал сақтаңыз:
1. Есепті түсінгенге дейін есеп текстісін оқып-зерттеу керек. Есептің барлық шарттары мен жетуге тиіс мақсаттарын түсінбей есепті шығарцға кіріспеңіз. Есепті шығаруға кіріспестен бұрын мына сұрақтарға жауап беріңіз: Не берілген? Есеп шарттары неде? Не табу керек немесе не дәлелдеу керек? М.Қашқари сөзімен айтқанда «Бастамастан бұрын, мақсатыңды ойлаңыз».
Есеп санада анық және түпкілікті орныққаннан кейін ғана оны шығаруды бастау керек. Есепті шығару үшін оған деген құлшыныс пен қажетті жігерлілік, шыдамдылық қажет.
«Ақылдың шығармашылық мүмкіндігі энтуализм мен ерік күші болмаған жерде дәрменсіздік жасайды», - дейді А.Андронов.
2. Есеп қарапайым түрден гөрі, көбіне, өзгертіліп беріледі. Сондықтан
оны түрлендіріп, бұрынна белгілі есепке, мәселеге келтіруге талаптаныңыз. Ол үшін берілген есепте бұрыннан белгілі не бар, соны пайдаланыңыз. Егер оны көрмесеңіз есепті басқаша тұжырымдаңыз да осы мақсатты қайтадан алдына қойыңыз.
3. Егер есеппен қандай да бір геометриялық фигура байланысты болса оны сызып, мүмкіндігінше берілгендері мен ізделінді шамаларды көрсету керек. Олардың байланысын табу қажет. Тиімді және қажет символдар мен белгілеулерді пайдаланыңыз. Қате немесе дұрыс емес чертеж кейде жалған жолға салып, ақиқат емес пікірге әкелуі мүмкін. Алғашқы чертежіңіз тиімсіз болса дұрыстап қайта сызыңыз. Д.Пойа бұл туралы: «Ақылды өз шешімін өзгертеді, ақымақ өзгертпейді», - дейді. Чертеж есептің көрнекілігіне көмектескенімен, қорытынды жасаудың негізі бола алмайды. Қорытындылар логикалық байланыстар негізінде ғана жасалады. Есеп шығарудың шын көрнекілігі бейнелер арасындағы өзара байланысты табуда.
Геометриялық емес есептерді шығаруда да көрнекілік құралы ретінде чертежді пайдаланғаныңыз дұрыс.
4. Есепті шеше отырып, әрбір қадамыңның дұрыстығын қадағалаңыз. Мысалы, түрлендіруде, есептеуде, салуда, теореманы дұрыс пайдалануда. «Сынамаған – алданар, ойланбаған - ұтқызар»,-дейді М.Қашқари.
5. Есепті шешу барысында берілгендері түгел пайдаланылды ма – осыны қадағалаңыз.
6. Есепті шешу барысында томаға тұйыққа тірелсеңіз, нәтижеңізді есеп талабымен және жолшыбай кездескен қосымша мақсаттармен салыстырыңыз. Осындай бір ғана көз жүгірту кейде есепті шешу жолының дұрыстығын байқатады.
7. Жалған пікірлерді, сол сияқты оған сүйеніп басқа бір пікірлерді дәлелдеу мүмкін емес. Сондықтан оны байқасаңыз қадамыңызды қайта тексеріңіз де түзетіңіз. Қате жібермей қайшы қорытындыға келсеңіз, бастапқы пікірді дәлелдегеніңіз. Дәлелдемекші пікірдің жалғандығын сезінесіңіз, дербес жағдайлар оны растаңыз.
8. Кейбір есептерді шығару үшін мағыналы логикалық талқылау да жеткілікті. Кейбір есептерді шешу ойлап табуға да, тапқырлыққа да тәуелді.
9. Жұмысты орындауда математиканың бір тарауынан алған біліміңізді екінші тарауына толық пайдалануыңызға болады, негізгі мақсат – есепті дұрыс, тиімді тәсілмен шығару. Есепті бір тәсілмен шығарғаннан гөрі, бір есепті бірнеше тәсілмен шығарған пайдалы. Өйткені, есеп таныс, сақсат түсінікті, тек оған басқа мәселелерді қолдану ғана қалды. Мәселен, мына есепті шығарайық:
Мысалы,
Катеттерінің қосындысы 10-ға тең тең тік бұрышты үшбұрыштың ауданы ең үлкен болуы үшін катеттерінің әрқайсысы қандай болуы керек және ол аудан неге тең болады?
Геометрияның бұл есебін шешуде алгебралық тәсілді пайдалануға болады: 
Жүйенің бірінші теңдеуінен в -ны тауып екіншісіне қойсақ, 
Бұдан аудан ең үлкен мәнін а=5 болғанда қабылдайтынын көреміз.
Жауабы: а=5, b=5,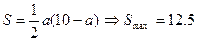 
Туындыны білетін оқушы есепті былай шешеді:
Немесе 
Егер 
болса, онда 
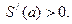
Егер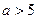 
болса, онда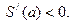 
Демек, а=5 нүктесінен өткенде туынды таңбасы плюстен минуске өзгереді. Демек, S функцифсы а=b=5 нүктесінде өзінің максимумын қабылдайды.
а=5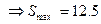 
(кв.бірлік)
Бұл есепті шығару үшін қосындысы тұрақты болатын екі санның көбейтіндісі өзінің ең үлкен мәнін көбейткіштер өзара тең болғанда қабылдайтынын білу де жеткілікті:
(а=b=5). 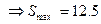(кв.бірлік)
Жалпы алғанда есеп машықтану жаттығулары ретінде оқушылардың зерделілігін кеңейту және логикалық ойлауын дамыту мақсаттары ретінде шығарылады. Осы жұмыста мақсаттар сыбайластырыла қарастырылады.
Енді есеп шығарудың кейбір тәсілдерін қарастырайық:
