Вопросы к экзамену по алгебре и геометрии (I семестр)
Вопросы I уровня.
Матрицы, определители. СЛУ.
1. Что называется матрицей? Перечислите линейные операции над матрицами. Приведите примеры.
2. Что называется произведением матриц? Любые ли две матрицы можно перемножить?
3. Какая матрица называется обратной для данной матрицы А? Всегда ли существует обратная матрица?
4. Сформулируйте правило нахождения А-1.
5. Какая матрица называется симметрической, кососимметрической? Приведите примеры.
6. Дайте определение минора и алгебраического дополнения элемента матрицы А. Для любой ли матрицы определено это понятие? Приведите примеры.
7. Дайте определение определителя п -го порядка.
8. Какие вы знаете способы вычисления определителя? Приведите примеры.
9. Что называется решением системы линейных уравнений? Какая система называется совместной, несовместной, определенной, неопределенной?
10. Какие системы называются эквивалентными (равносильными)? Какие преобразования системы приводят ее к эквивалентной? Каким преобразованиям расширенной матрицы они соответствуют?
11. Какая система называется квадратной? Какие вы знаете методы решения таких систем? Можно ли их назвать методами исследования и решения системы?
12. Сформулируйте правило Крамера решения СЛУ. Любую ли систему можно решить методом Крамера?
13. В чем заключается матричный метод решения СЛУ? Для каких систем он применим?
14. В каком случае квадратная система линейных однородных уравнений имеет единственное решение? Какое это решение?
15. В каком случае квадратная система линейных однородных уравнений имеет ненулевое решение?
2. Линейные пространства (ЛП).
16. Дайте понятие линейного пространства. Приведите примеры.
17. Что называется линейной комбинацией системы векторов ЛП? Приведите пример.
18. Какая система векторов ЛП называется линейно зависимой? Приведите пример.
19. Какая система векторов ЛП называется линейно независимой? Приведите пример.
20. Какая система векторов ЛП называется максимально линейно независимой? Приведите пример.
21. Что называется базисом ЛП? Приведите пример.
22. Приведите пример базиса в V2, V3.
23. Дайте понятие п -мерного вектора, пространства R n (арифметического пространства).
24. Как определяются линейные операции над векторами R n? Приведите пример.
25. Приведите пример базиса в R n.
26. Сформулируйте теорему о разложении вектора ЛП по базису.
27. Дайте понятие координат вектора в заданном базисе. Приведите пример.
28. Дайте понятие минора матрицы. Для какой матрицы определено это понятие? Приведите пример.
29. Дайте определение ранга матрицы. Приведите пример. Перечислите свойства ранга.
30. Какие вы знаете способы нахождения ранга матрицы?
31. Сформулируйте Теорему Кронекера-Капелли.
32. Что значит исследовать СЛУ? Какие вы знаете способы исследования СЛУ? Приведите пример.
33. В каком случае и как неизвестные СЛУ разделяются на базисные и свободные?
34. В каком случае СЛУ имеет бесконечное множество решений. Приведите пример.
35. Дайте понятие общего решения СЛУ. В каком случае это понятие существует? Какое решение СЛУ называется частным решением?
36. В каком случае произвольная СЛУ имеет единственное решение? Приведите пример.
Векторная алгебра
37. Что называется геометрическим вектором? модулем вектора?
38. Дайте понятие проекции вектора на числовую ось.
39. Что такое орт вектора, орт числовой оси? Как выражается вектор через его орт и наоборот?
40. Какие векторы в V2, V3 называются коллинеарными, ортогональными, компланарными? Приведите примеры.
41. Какие векторы образуют базис в V2, в V3?
42. Какой базис в V2, V3 называется ортонормированным? Приведите примеры.
43. Дайте понятие декартовой прямоугольной системы координат в V2, V3.
44. Чему равны координаты вектора в декартовой системе координат? Приведите пример.
45. Как относительно друг друга расположены векторы ` i,` j,` k? Каковы их координаты?
46. Сформулируйте и запишите условие коллинеарности двух векторов. Каким является это условие?
47. Дайте определение скалярного произведения двух векторов.
48. Сформулируйте и запишите условие ортогональности двух векторов. Каким является это условие?
49. Как выражается скалярное произведение двух векторов через их координаты?
50. Дайте определение векторного произведения двух векторов. Приведите пример.
51. Как выражается через координаты векторов их векторное произведение?
52. Как можно вычислить площадь параллелограмма, треугольника, построенного на двух векторах, как на сторонах?
53. Дайте определение смешанного (векторно-скалярного) произведения векторов.
54. Каков геометрический смысл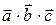 
?
55. Как выражается через координаты трех векторов их смешанное произведение?
56. Сформулируйте и запишите необходимое и достаточное условие компланарности трех векторов.
Аналитическая геометрия
1. В чем заключается предмет аналитической геометрии? Что является основой аналитической геометрии? Почему?
2. Сформулируйте основные задачи аналитической геометрии. Приведите пример решения одной из них.
3. Дайте определение уравнения линии на плоскости, уравнения плоскости в пространстве. Приведите пример.
4. Какие вы знаете виды уравнений прямой на плоскости? От чего зависит вид уравнения? Выведите общее уравнение прямой на плоскости.
5. Каким характерным признаком в декартовой системе координат отличается уравнение прямой от уравнений других линий?
6. Как расположена прямая относительно системы координат, если в ее общем уравнении отсутствует: а) свободный член, б) одна из переменных, в) одна из переменных и свободный член? Ответ обоснуйте, приведите пример.
7. Выведите каноническое уравнение прямой на плоскости, канонические уравнения прямой в пространстве. Как перейти от канонических уравнений к общим?
8. Какие вы знаете уравнения плоскости в пространстве? Отчего зависит вид уравнения? Выведите общее уравнение плоскости. Каким характерным признаком отличается уравнение плоскости в декартовых координатах от уравнений других поверхностей?
9. Как расположена плоскость относительно системы координат, если в ее общем уравнении отсутствует: а) свободный член, б) одна из переменных, и) две переменных, г) одна из переменных и свободный член, д) две переменные и свободный член?
10. Запишите уравнение плоскости в отрезках. Каков геометрический смысл коэффициентов этого уравнения? Как перейти от общего уравнения плоскости к уравнению в отрезках и наоборот?
11. Сформулируйте условия параллельности, перпендикулярности, совпадения двух прямых на плоскости, двух плоскостей в пространстве, прямой и плоскости.
12. Какие вы знаете виды уравнений прямой в пространстве? От чего зависит вид уравнений?
13. Запишите общие уравнения прямой в пространстве. Как перейти от общих уравнений к каноническим?
14. Сформулируйте условия пересечения двух прямых в пространстве, заданных каноническими уравнениями.
15. Дайте определение эллипса, гиперболы. Запишите их канонические уравнения. При каком расположении этих кривых относительно системы координат получаются эти уравнения? Каков геометрический смысл и названия коэффициентов этих уравнений?
16. Дайте определение параболы, запишите каноническое уравнение. При каком расположении параболы относительно системы координат получается это уравнение? Каков геометрический смысл коэффициента этого уравнения?
17. Какие линии на плоскости называются кривыми второго порядка? Запишите общее уравнение кривых второго порядка. Назовите эти кривые.
18. Как по общему уравнению кривых второго порядка определить, какую именно кривую оно определяет? Сформулируйте алгоритм исследования уравнения вида:
а) А х 2 +С у 2 + D x + E y + F = 0, б) А х 2 + 2B xy +С у 2 = 0? Приведите примеры.
19. Дайте определение поверхности вращения. Приведите пример такой поверхности, запишите её уравнение.
20. Дайте определение цилиндрической поверхности. Приведите пример такой поверхности, запишите её уравнение.
21. Перечислите поверхности второго порядка и их канонические уравнения.
Комплексные числа. Многочлены.
22. Дайте понятие комплексного числа. Какие числа называют комплексно-сопряженными, противоположными? Приведите примеры. Дайте геометрическую интерпретацию.
23. Дайте определение модуля и аргумента комплексного числа z = x + iy. Как они обозначаются? Как найти модуль, аргумент? Приведите пример.
24. Какие формы записи комплексного числа вы знаете? Как осуществляется переход от одной формы к другой? Приведите пример.
25. Какие операции можно выполнять над комплексными числами? Какие из перечисленных операций можно выполнять только в алгебраической форме, какие нельзя выполнять в алгебраической форме?
26. Какую операцию можно выполнить только в тригонометрической форме? Определите эту операцию, приведите пример.
27. Какие операции над комплексными числами можно выполнять в любой форме записи? В каком случае рациональнее пользоваться той или иной формой? Приведите примеры.
28. Дайте понятие многочлена (полинома) от одной неизвестной. Приведите пример многочлена четвертой степени с действительными коэффициентами, пример многочлена нулевой, первой степени.
29. Дайте понятие равенства двух многочленов, приведите примеры.
30. Дайте определение суммы и произведения двух многочленов, произведение многочлена на число. Приведите примеры.
31. Сформулируйте теорему о делении многочлена на многочлен с остатком, приведите пример. Дайте понятие частного, остатка
32. Дайте определение корня многочлена. Сформулируйте необходимое и достаточное условие, при котором число С есть корень многочлена.
33. Дайте понятие кратного корня. Может ли многочлен с действительными коэффициентами иметь комплексный корень? Что вы знаете о комплексных корнях таких многочленов?
34. Что значит разложить многочлен на множители? В каком случае многочлен с действительными коэффициентами разлагается на линейные множители с действительными коэффициентами?
35. В каком случае многочлен с действительными коэффициентами можно разложить на неприводимые множители первой и второй степени? Приведите примеры.
36. Дайте понятие рациональной дроби. Какая рациональная дробь называется правильной, неправильной?
37. Что значит выделить целую часть неправильной рациональной дроби? Приведите пример.
38. Какие рациональные дроби называются простейшими (элементарными)?
39. Сформулируйте алгоритм разложения правильной рациональной дроби на сумму простейших.
Образец экзаменационного билета на оценку «удовлетворительно»
1. Докажите, что система 
имеет нетривиальные решения. Найдите их.
2. В треугольной пирамиде АВСD найдите вектор 
.
3. Как расположена плоскость 4 у +5 z -2=0 относительно системы координат? Постройте эту плоскость.
4. Вычислите 
5. Построить кривую 
6. Что называется матрицей? Приведите пример прямоугольной, диагональной матриц.
7. Сформулируйте теорему Кронекера-Капелли. Что значит исследовать СЛУ?
8. Дайте определение векторного произведения векторов. Как найти векторное произведение, если известны координаты векторов?
9. Запишите известные вам уравнения прямой в пространстве и назовите их.
10. Какие рациональные дроби называются простейшими?
Вопросы II уровня
1. Матрицы, определители. СЛУ
1. Что можно сказать о матрицах А и В, если существуют АВ, ВА и АВ = ВА?
2. Как изменится произведение АВ матриц А и В, если переставить i -ю и j -ю строки матрицы А?
3. Как изменится произведение АВ матриц А и В, если переставить i -й и j -й столбцы матрицы В?
4. Что общего и в чем различие диагональной и единичной матриц?
5. Как изменится определитель, если к каждой его строке, кроме последней, прибавить последнюю?
6. Как изменится определитель, если его первый столбец поставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение?
7. Какая матрица называется ортогональной? Приведите пример.
8. Если А – симметрическая матрица, то какой будет А-1? Почему?
9. Как изменится обратная матрица А-1, если в матрице А i -ю строку умножить на число С ¹ 0?
10. Доказать, что (АВ)-1 = В-1А-1.
11. Доказать, что любую матрицу А можно представить в виде А = В + С, где В – симметрическая, а С – кососимметрическая матрицы.
2. Линейные пространства (ЛП)
1. Будет ли линейно независимой система векторов, содержащая два равных вектора? Почему?
2. Будет ли линейно независимой система векторов, содержащая нулевой вектор? Почему?
3. Образует ли ЛП множество всех векторов трехмерного пространства, координаты которых есть целые числа?
4. Образует ли ЛП множество векторов V3, лежащих на оси ОZ?
5. Образует ли ЛП множество векторов V2, лежащих на биссектрисе I и III координатных углов?
6. Образует ли ЛП множество векторов V3, исходящих из начала координат?
7. Образует ли ЛП множество всех произвольных квадратных матриц?
8. Образует ли ЛП множество всех матриц вида 
?
9. Дайте определение ранга матрицы. Как изменится ранг матрицы, если переставить местами две ее строки или два столбца?
10. Как изменится ранг матрицы, если приписать к ней один столбец?
11. Как изменится ранг матрицы, если приписать к ней два произвольных столбца?
12. Составить матрицу, ранг которой равен 3.
13. Что можно сказать о квадратной СЛУ, если ее ранг меньше числа неизвестных?
14. Если система линейных неоднородных линейных уравнений имеет нетривиальное решение, то сколько всего имеет решений эта система? Приведите пример.
15. Что называется фундаментальной системой решений однородной СЛУ? Сформулируйте алгоритм нахождения ФСР.
16. Почему для нахождения общего решения однородной системы достаточно найти ФСР? Как записывается общее решение?
17. Дана СЛУ 
. Будет ли система 
, 
ФСР заданной СЛУ?
18. Дана СЛУ 
. Будет ли система а 1 = (2,0,1), а 2 = (0,0,0) представлять ФСР заданной СЛУ?
19. 
Дана СЛУ 
. Будет вектор а 1 = (2,0,1) представлять ФСР?
20. Что значит «разложить вектор по базису»? Разложите вектор ` с, изображенный на рисунке, по базису ` а,` b
21. Разложите вектор ` с = (2,-3)по базису ` е 1=(2,1), ` е 2=(0,-4).
Векторная алгебра
22. Пусть 
. Верно ли, что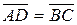 
? Приведите пример.
23. Какому условию должны удовлетворять векторы 
и 
, чтобы вектор + делил пополам угол между векторами и ?
24. Как следует направить векторы ` а и` b, чтобы длина ` а +` b была наибольшей? Наименьшей?
25. Каким условиям должны удовлетворять векторы ` а и` b, чтобы имели место соотношения 
и 
?
26. Коллинеарные ли векторы ` а и` b, если векторы` а +` b и` а –` b параллельны?
27. Дайте определение произведения вектора на действительное число. При каких значениях k длина вектора k× ` a (` a ¹ 0),больше длины ` a? Меньше длины ` a?
28. При каких значениях m вектор ` a = (2, m) равен вектору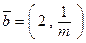 
?
29. При каких значениях a точки А(3,2) и В(a,-1) расположены на одной прямой, параллельной оси ОУ?
30. При каких значениях a точки А(3,2) и В(a,-1) расположены на одинаковом расстоянии от оси ОУ?
31. Какой угол образует вектор ` a = (cosa, sina) с ` i, c ` j? Какой это вектор?
32. Может ли вектор пространства составлять с осью ОХ угол 30о, а с осью OZ угол 45о?
33. Каким условиям удовлетворяет угол между векторами` а и` b, если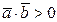 
; 
?
34. Следует ли из равенства ` а × ` е =` b × ` е, где ` е – единичный вектор, равенство` a = ` b?
35. Параллельны ли прямые, проходящие соответственно через точки (1,-1), (2,1), (3,5), (1,-3)?
36. Каков геометрический смысл равенства [ a – b, a + b ] = 2[ a, b ]?
37. Какому условию должны удовлетворять векторы ` a,` b,` c, если (a,` b,` c)>0? (a,` b,` c)<0?
Аналитическая геометрия
38. Как вы понимаете слова «составить уравнение геометрического объекта»?
39. Дайте определение углового коэффициента прямой на плоскости. Какие вы знаете виды уравнения прямой с угловым коэффициентом? Существуют ли аналогичные уравнения прямой в пространстве? Почему?
40. При каких значениях р прямая (р + 2) х + (р 2 - 9) у + 1 = 0 будет: параллельна оси ОХ; параллельна оси ОУ; проходить через начало координат?
41. При каких значениях р прямые х - 2 у + р = 0 и х - ру - 2 =0 пересекаются?
42. При каких значениях р прямые а) 2 х + ру + 4 = 0 и 4 х -5 у + 5 = 0 параллельны; б) 4 х - ру + 2 =0 и х + ру - 2 = 0 перпендикулярны; в) рх - у - р = 0 и 4 х - ру -4 = 0 совпадают?
43. Является ли уравнение ½ х ½+½ у ½= 0 уравнением прямой на плоскости? Почему? Какой геометрический образ имеет это уравнение? Сделайте чертеж.
44. Какой геометрический образ на плоскости имеет уравнение½2 х- 1½= 0? Сделайте чертеж.
45. При каких значениях а прямая 
проходит через начало координат?
46. Всегда ли угол между прямыми на плоскости равен углу между двумя векторами, перпендикулярными к этим прямым? Ответ обоснуйте.
47. Какой геометрический образ имеет уравнение 2 х - у +4+ ½ z ½-1=0? Сделайте чертеж.
48. Какие возможны случаи расположения трех прямых на плоскости? Сформулируйте соответствующие условия.
49. Какие возможны случаи расположения трех плоскостей в пространстве? Сформулируйте соответствующие условия.
50. Приведите геометрическое истолкование системы m линейных уравнений с двумя переменными, если а) система совместна и определенна; б) система совместна и неопределенна; в) система не совместна.
51. Приведите геометрическое истолкование системы m линейных уравнений с тремя переменными, если а) система совместна и определенна; б) система совместна и неопределенна; в) система не совместна.
52. 
Сформулируйте условие изображенного на рисунке расположения трех прямых на плоскости
 |
53.Запишите условия, при которых прямая 
принадлежит плоскости А x + D y + C z + D = 0.
54.Каким геометрическим свойством обладают точки плоскости, координаты которых удовлетворяют уравнению а) 2 х 2 + у 2 + 4 у = 0, б) х 2 - у 2 -4 х + 8 = 0. Проиллюстрируйте на чертеже.
55.Каким геометрическим свойством обладают точки плоскости, координаты которых удовлетворяют уравнению а) у 2 = 4(х - 1), б) х 2 = -2 у - 8. Проиллюстрируйте на чертеже.
56.При каких значениях п прямая х = п пересекает кривые а) 
;б) 
?
57.Каким общим геометрическим свойством обладают кривые второго порядка? Проиллюстрируйте на чертеже.
58.Сформулируйте оптическое свойство параболы, эллипса. Докажите.
