ln x dx, x ln(x – 1) dx, x e2x dx, x2cos x dx, ex sin x dx, arcsin x dx

Рациональные алгебраические дроби.

Основная теорема алгебры:

P_n(x) = xⁿ + a_n–1xⁿ⁺¹ + a_n-2xⁿ⁺² +... + a₀ = (x - a₁) (x - a₂)... (x - a_n)

{ Пр. ax² + bx + c = a(x –x₁)(x – x₂) }

Полином n – ой степени всегда можно представить как произведение n двучленов

(x - a_i), где a_i -корни полинома. Корни могут быть действительными числами, комплексными числами, кратными. Комплексные корни входят сопряженными парами

a = a + ib, a* = a - ib и произведение

(x - a)(x - a*) = (x – a – ib)(x – a + ib) = (x – a)² + b² = x² + px + q,

где D < 0, включает только действительные числа. В общем случае

P_n(x) = (x - a₁)^k₁(x - a₂)^k₂... (x² + p₁x + q₁)^r₁..., где k₁+k₂+...+2(r₁+r₂...) = n.

Рациональная алгебраическая дробь наз. правильной, если n < m.Если n > m, то из дроби выделяют целую часть и остаток в виде правильной дроби

= , где k < m

Выделение целой части: 1) - метод добавления числа

2) деление полиномов уголком = (x + 6) +

 

Простейшие дроби: , , , , где D < 0

Интегрирование простейших дробей:

1) J₁ = ò dx = A ò = A ln (x – a) + C

2) J₂ = ò dx = B ò = B ò = B + C

3) J₃ = ò dx, D < 0. Алгоритм решения:

1. трехчлен приводят к полному квадрату x²+px+q = (x+p/2)² + (q–p²/4);

2. замена переменных t = x + p/2; 3. переход к сумме двух интегралов вида

J_a = = = , J_b = =

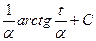
4) J₄ = ò dx. Повторим алгоритм решения и придем к интегралам

J `<sub>a</sub> = = , J `_b = . Если применить к интегралу J_b интегрирование по частям, то получим =

Пр. J = 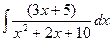; D = -36 < 0,

 

Решение: 1) x² + 2x + 10 = x² + 2x + 1 + 9 = (x + 1)² + 3² ;

2) пусть t = x + 1, тогда x = t – 1, dx = dt, x² + 2x + 10 = t² + 3²,

3) J = = + 2 = 3/2 ln|t² + 3²| + 2/3 arctg t/3 + C

= 3/2 ln| x² + 2x + 10| + 2/3 arctg (x – 1)/3 + C

Пр. J = = =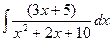

= = + 2 = 3/2 ln|t² + 3²| + 2/3 arctg t/3 + C

Разложение дроби на простейшие.

А) Корни знаменателя алгебраической дроби - действительные числа.

Тогда он разлагается на произведение только двучленов R_m(x) = (x - a₁)(x - a₂)²(x - a₃)³.. и дробь можно представить как сумму m простейших дробей.

Однократному корню соответствует одна дробь . Двукратному - две дроби:

+ . Трехкратному - три дроби: + +

= + + + + + +...

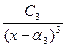
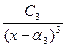Действительно, сложение простейших дробей приведет к общему знаменателю R_m(x), а в числителе образуется некоторый полином T_n(x). При определенных значениях коэффициентов А, B_i, C_i T_n(x) = P_n(x). Такое разложение дроби на сумму простейших дробей наз. м етодом неопределенных коэффициентов.

Вычисление коэффициентов.

1 способ. Приравняем коэффициенты в T_n(x) и P_n(x) при одинаковых степенях х, получим полную систему n линейных уравнений, решение системы дает А, B_i, C_i

Пр.2.

x¹ | A + B = 2 Þ A = -5

x⁰ | -2A – B = 3 Þ B = 7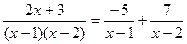

2 способ. В уравнении T_n(x) = P_n(x) последовательно заменяем х на a_i и сразу получаем значения коэффициентов.

В Пр.2.

пусть х = 1, тогда 5 = - A Þ A = -5

пусть х = 2, тогда 7 = B Þ B = 7

Б) Корни знаменателя алгебраической дроби - сопряженные комплексные числа.

Тогда он разлагается на произведение трехчленов x²+px+q, где D < 0, и дробь можно представить как сумму простейших дробей. Однократному трехчлену соответствует одна дробь . Двукратному - две дроби: + .

Пр.3.

x² | A + M = 0; x¹ | N – M = 2; x⁰ | 4A - N = 1 Þ A = 3/5; M = -3/5; N = 7/5.

 

Интегрирование тригонометрических функций.

Интегралы типа sin^mx cosⁿx dx, где m или n НЕчетное число (8)

Метод подведения под знак дифференциала

Пр. sin³x dx = sin²x sin x dx = - (1-cos²x)d(cos x) = - (1–t²)dt = -cos x + cos³x/3 +C

sin²x cos x dx,

Интегралы типа sin^mx cosⁿx dx, где m и n четные числа (9)

Метод понижения степени по формулам

sin²x = ½ (1 – cos 2x); cos²x = ½ (1 + cos 2x); sin x cos x = ½ sin 2x

или замена tg x = t (см. ниже)

Пр. sin²x dx = ½ (1 – cos 2x) dx = ½ dx - ¼ cos 2x d(2x) = x/2 - ¼ sin 2x +C

sin²x cos²x dx, cos⁴x dx

Интегралы типа sin ax cos bx dx по формулам (10)

 

sin a cos b = ½[sin(a+b) + sin(a-b)]; cos a cos b = ½[cos(a+b) + cos(a-b)]

sin a sin b = ½[cos(a-b) – cos(a+b)]

Пр. sin 3x cos x dx = ½ (sin 4x + sin 2x)dx = -1/8 cos 4x - ¼ cos 2x + C

sin 5x cos 3x dx

Интегралы типа R(tg(x), sin²ⁿ x, cos^2mx) dx Замена tg x = t, тогда (11)

= (1 + tg²x) dx = dt dx = dt/(1+t²), x = arctg t

cos²x = = , sin²x = (1 – cos²x) =

Пр. tg³x dx = t³/ (1+t²) dt = (t³ + t – t)/ (1+t²) dt = t dt - t/(1+t²) dt =

= t²/2 - ½ d(1+t²)/ (1+t²) = ½ tg²x – ½ ln |1+tg²x| + C

Пр. = = (t ^-4 + t ^–2) dt = - (tg x)^-3 /3 - (tg x) ^–1 + C

Универсальная замена tg x/2 = t в интегралах R(sin x,cos x) dx удобна, когда sin x, cos x входят в R() в 1-ой степени,тогда sin x = , cos x = , dx =

и приходим к интегралу от рациональной алгебраической дроби.

{ sin x = 2sin x/2 cos x/2 = 2 cos²x/2 = ; (12)

cos x = cos²x/2 – sin²x/2 = cos²x/2 (1 - ) = cos²x/2 (1 – t²) = }

Пр. = { 1 + sin x = 1 + = } = 2 =

C

;

 

Интегрирование иррациональных функций.

Опр. Функция наз. иррациональной, если она содержит аргумент, различные корни из аргумента и выражения с аргументом.

Пр. ,

Интегралы типа R( x, , ,... ) dx (13)

Для всех показателей корней найдемНОК (k₁, k₂,..., k_m) = n, тогда все n/k_i -целые числа и подстановка x = tⁿ исключит все корни.

Пр. J = = { НОК(2,3) = 6, пусть x = t⁶, тогда dx = 6t⁵dt, t = x^1/6 } =

= = 6 = 6 =

= 6(t³/3 - t²/2 + t) – 6 ln |t + 1| + C = 2 x^1/2 - 3 x^1/3 + 6 x^1/6 - 6 ln | 1 + x^1/6 | + C

Линейная иррациональность R( x, , ,... ) dx (14)

Находим НОК(k₁, k₂,..) = n, подстановка ax + b = tⁿ, тогда dx = (n/a)t^{n – 1}dt, x =(tⁿ – b)/a и функция становится рациональной.

Пр. J = = { НОК(1,2) = 2, пусть 3 – x = t², тогда dx = - 2 tdt, x = 3 – t² }= = - 2 = -6 t³/3 + 2 t⁵/5 + C = -2 (3 – x)^1/2 + 2/5 (3 – x)^5/2 + C

;

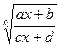Дробно-линейная иррациональность R( x, , ,... ) dx (15)

Находим НОК(k₁, k₂,..) = n, делаем подстановку = tⁿ, функция становится рациональной.

Пр. J = = { пусть = t², тогда x = , dx = } =

= 2 ; Þ A = B = D = ¼, C = - ¼;

J = ¼ { ln| t –1 | - ln| t+1 | - (t – 1)^-1 – (t + 1)^-1 } + C

Интегралы типа R( x^m, ) x^{m -1} dx (16)

Сочетание элементов x^{m – 1}dx и x^m позволяет перейти к дифференциалу d(x^m) или d(ax^m + b), а замена ax^m+ b = tⁿ избавляет от иррациональности.

Тогда x^m-1 dx = n t^n-1 dt/a, x^m = (tⁿ-b)/a.

Пр. J = ₌ { пусть 2x²+1 = t³, тогда xdx = ¾ t² dt, x² = ½(t³-1) } =

= ¾ ½ (t³-1)t² dt/t = 3/40 t⁵ – 3/16 t² + C

Квадратичные иррациональности.Тригонометрические подстановки. (17)

А) R( x, ) dx; Б) R( x, ) dx; В) R( x, ) dx

т.е. под корень входит х² .

 

А) : замена x = a sin t Þ a² – x² = a² (1 – sin² t) = a² cos²t, = a cos t

t = arcsin (x/a), dx = a cos t dt

 

Б) : замена x = a tg t Þ a² + x² = a² (1 + tg² t) = a² / cos²t, = a / cos t

t = arctg (x/a), dx = a dt / cos² t

В) : замена x = a / cos t Þ x² – a² = a² (1 / cos² t – 1) = a² tg²t, = a tg t

t = arcos (a/x), dx = - a sin t dt / cos² t

Пр. J = = { пусть x = 2 sin t, тогда dx = 2 cos t dt, = 2 cos t }=

= - ctg t - t + C = - ctg (arcsin(x/2)) - arcsin(x/2) + C

 

Пр. J = = { пусть x = 2 tg t, тогда dx = 2 dt / cos² t, = 2/cos t }=

= 8 - 8 8/3 cos^-3 t + C = 8/3 cos^-3(arctg(x/2))+ C

 

Пр. J = = { пусть , тогда , = 2 tg t } =

= - = - ½ = - ¼ = - ¼ (t - ) + C =

= - ¼ [ arcos (2/x) + ½ sin (2(arcos(2/x))) ] + C

 

 

Квадратичные иррациональности.Общий случай. (18)

Интегралы типа R( x, ) dx Необходимо:

1) Привести трехчлен к полному квадрату: ax² + bx + c = a[ x² + px + q ] =

= a[ x² + 2x(p/2) + (p/2)² - (p/2)² + q] = a [ (x + p/2)² + (q – p²/4) ], где p = b/a, q = c/a. 2) Замена переменных: пусть x + p/2 = z, тогда ax² + bx + c = |a|{ ± z² + (q – p²/4)}

и переходим к одному из трех случаев: А), Б), В)

 

Пр. J = = { x² + 2x –3 = (x +1)² – 4 = t²- 2², где t = x +1, тогда dx = dt }

= = { (В): пусть , тогда , } =

= -4 = -4 ; +

Þ A = B = D = ¼, C = - ¼; J = - { ln + 2 }+ C, где z = arccos .